9 класс АЛГЕБРА Урок № __
Тема: Решение систем уравнений второй степени.
Цель: рассмотреть способ подстановки для решения систем уравнений.
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга. Выявляются отсутствующие
II. Сообщение темы и цели урока
III. Повторение и закрепление раннее пройденного материала
1. Проверка выполнения домашнего задания
2. Контроль усвоения материала
Вариант I
1. Графически решите систему уравнений 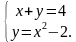
2. Для каждого значения параметра а найдите число решений системы уравнений 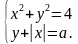
Вариант II
1. Графически решите систему уравнений 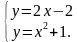
2. Для каждого значения параметра а найдите число решений системы уравнений 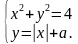
IV. Изучение нового материала
Рассмотрим теперь аналитическое решение систем уравнений с двумя переменными. Наиболее распространённый способ решения систем – способ подстановки. Для этого необходимо:
1) выразить из более простого уравнения одну переменную через другую;
2) подставить это выражение в другое уравнение и получить уравнение с одной неизвестной;
3) решить полученное уравнение с одной переменной;
4) найти соответствующие значения второй неизвестной.
Пример 1
Решим систему уравнений 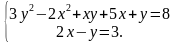
Второе уравнение системы является линейным (первой степени) и, соответственно, более простым. Выразим из него переменную у через переменную х: у = 2х – 3. Подставим это уравнение в первое уравнение и получим уравнение с переменной х:
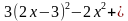 х(2х – 3) + 5х + (2х – 3) = 8, или (после преобразований)
х(2х – 3) + 5х + (2х – 3) = 8, или (после преобразований) 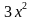 -8х+4=0. Корни этого квадратного уравнения: х1 = 2 и х2 =
-8х+4=0. Корни этого квадратного уравнения: х1 = 2 и х2 = 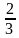 . Используя формулу у = 2х – 3, найдём соответствующие значения переменнной у: у1 = 2∙2 – 3 = 1 и у2 = 2∙
. Используя формулу у = 2х – 3, найдём соответствующие значения переменнной у: у1 = 2∙2 – 3 = 1 и у2 = 2∙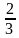 – 3 = -
– 3 = - 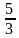 .
.
Итак, система имеет два решения: (2; 1) и 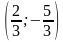 .
.
Во многих случаях оба уравнения системы являются нелинейными. Иногда способ подстановки пригоден и для таких систем.
Пример 2
Решим систему уравнений 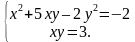
Очевидно, что х ≠ 0. Из второго уравнения выразим переменную у через х: у = 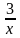 и подставим в первое. Получаем уравнение
и подставим в первое. Получаем уравнение 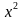 + 5∙3 – 2∙
+ 5∙3 – 2∙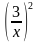 = -2, или (после преобраований)
= -2, или (после преобраований) 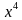 +17
+17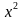 -18=0. Корни этого биквадратного уравнения: х1 = 1 и х2 = -1. По формуле у =
-18=0. Корни этого биквадратного уравнения: х1 = 1 и х2 = -1. По формуле у = 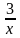 найдём соответствующие значения у: у1 =
найдём соответствующие значения у: у1 = 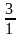 = 3 и у2 =
= 3 и у2 = 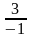 = -3. Итак, система уравнений имеет два решения: (1;3) и (-1;-3).
= -3. Итак, система уравнений имеет два решения: (1;3) и (-1;-3).
Способ подстановки полезен и при решении систем уравнений с параметрами.
Пример 3
При всех значениях параметра а определите число решений системы уравнений 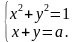
Из второго уравнения выразим переменную у через х: у = а + х. Подставим это выражение в первое уравнение и получим: 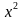 + (а – х)2 = 1, или
+ (а – х)2 = 1, или 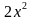 - 2ах + а2 – 1 = 0. Дискриминант этого квадратного уравнения D = 4(2 - а2). Число решений уравнения (а следовательно, и системы уравнений) определяется знаком дискриминанта.
- 2ах + а2 – 1 = 0. Дискриминант этого квадратного уравнения D = 4(2 - а2). Число решений уравнения (а следовательно, и системы уравнений) определяется знаком дискриминанта.

Если D 0, или а ∈ (-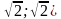 , система имеет два решения (пересечение прямой и окружности – случай а).
, система имеет два решения (пересечение прямой и окружности – случай а).
Если D = 0, или а ∈  , система имеет одно решение (касание прямой и окружности – случай б).
, система имеет одно решение (касание прямой и окружности – случай б).
Если D или а ∈ (-∞;- ⋃(
⋃( , система не имеет решений (прямая не пересекает окружность – случай в).
, система не имеет решений (прямая не пересекает окружность – случай в).
Заметим, что в ряде случаев при решении используют способ сложения (как частный случай способа подстановки).
Пример 4
Решим систему уравнений
Сложим уравнения системы и получим:  = 32, или
= 32, или  =4, откуда х+1 =
=4, откуда х+1 =  2 и х1 = 1 и х1 = -3. Подставим выражение
2 и х1 = 1 и х1 = -3. Подставим выражение  =4, например, в первое уравнение системы. Получим: 3 ∙ 4 - 2
=4, например, в первое уравнение системы. Получим: 3 ∙ 4 - 2 = 10, откуда
= 10, откуда  = 1, или у + 3 = 1 и у = -2.
= 1, или у + 3 = 1 и у = -2.
Итак, система уравнений имеет два решения: (1; -2) и (-3; -2).
Остальные способы решения систем уравнений будут рассмотрены в конце главы.
V. Решение упражнений
№429; 431; 433 – 437; 443.
VI. Домашнее задание
№ 430; 432; 451.
VII. Оценивание







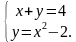
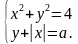
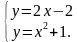
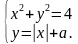
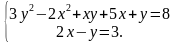
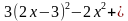 х(2х – 3) + 5х + (2х – 3) = 8, или (после преобразований)
х(2х – 3) + 5х + (2х – 3) = 8, или (после преобразований) 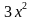 -8х+4=0. Корни этого квадратного уравнения: х1 = 2 и х2 =
-8х+4=0. Корни этого квадратного уравнения: х1 = 2 и х2 = 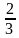 . Используя формулу у = 2х – 3, найдём соответствующие значения переменнной у: у1 = 2∙2 – 3 = 1 и у2 = 2∙
. Используя формулу у = 2х – 3, найдём соответствующие значения переменнной у: у1 = 2∙2 – 3 = 1 и у2 = 2∙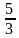 .
. 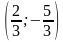 .
.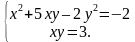
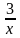 и подставим в первое. Получаем уравнение
и подставим в первое. Получаем уравнение 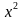 + 5∙3 – 2∙
+ 5∙3 – 2∙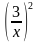 = -2, или (после преобраований)
= -2, или (после преобраований) 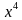 +17
+17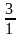 = 3 и у2 =
= 3 и у2 = 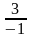 = -3. Итак, система уравнений имеет два решения: (1;3) и (-1;-3).
= -3. Итак, система уравнений имеет два решения: (1;3) и (-1;-3).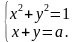
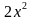 - 2ах + а2 – 1 = 0. Дискриминант этого квадратного уравнения D = 4(2 - а2). Число решений уравнения (а следовательно, и системы уравнений) определяется знаком дискриминанта.
- 2ах + а2 – 1 = 0. Дискриминант этого квадратного уравнения D = 4(2 - а2). Число решений уравнения (а следовательно, и системы уравнений) определяется знаком дискриминанта. 
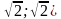 , система имеет два решения (пересечение прямой и окружности – случай а).
, система имеет два решения (пересечение прямой и окружности – случай а).









