Цели:
расширить знания учащихся о числе, способах его записи;
дать определение понятия «система счисления»;
вывести алгоритм перевода чисел из двоичной системы в десятичную и наоборот;
развить у учащихся логическое и алгоритмическое мышление, творческие способности и коммуникативные навыки;
создать условие для формирования и развития у учащихся интереса к изучению математики и информатики.
воспитание информационной культуры, внимания, аккуратности, усидчивости.
Оборудование:
доска;
лист с теорией;
карточки с заданиями.
Тип урока: урок открытия нового знания.
Вид урока: комбинированный урок.
Методы урока: репродуктивный.
План урока:
Организационный момент – 2 минуты;
Объяснение материала – 15 минут;
Закрепление материала – 20 минут;
Итоги урока – 2 минуты;
Дача домашнего задания – 1 минута.
Ход урока.
Организационный момент.
У: Здравствуйте, садитесь. Тема электива - Десятичная и двоичная системы счисления. Цель урока - познакомиться с понятием «система счисления», научиться переводить числа из двоичной системы в десятичную и наоборот.
У: Откройте тетради, запишите число 21.03 и тему урока - Десятичная и двоичная системы счисления.
Объяснение материала.
Система счисления – это система записи чисел, в которой используется алфавит или определенный набор цифр. (Ученики записывают данное определение в тетрадь)
Нас будут интересовать двоичная и десятичная системы счисления.
Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число цифр определяет основание системы счисления. Если число цифр — десять, то основание системы счисления равно десяти. В двоичной же системе существует всего две цифры: 0 и 1. Основание равно двум. Возникает вопрос, можно ли с помощью всего двух цифр представить любую величину. Оказывается, можно!
Развернутая форма записи числа.
Принцип записи чисел в десятичной системе счисления. Значение цифры в записи числа зависит не только от самой цифры, но и от места расположения этой цифры в числе (говорят: от позиции цифры). Например, в числе 333 первая справа цифра обозначает: три единицы, следующая — три десятка, следующая — три сотни. Этот факт можно выразить равенством:
33310 = 3 • 102 + 3 • 101 + 3 • 100 = 300 + 30 + 3 (Пример записан и разобран на доске)
В данном равенстве выражение, стоящее справа от знака «равно», называется развернутой формой записи многозначного числа. Вот еще пример развернутой формы записи многозначного десятичного числа:
825710 = 8 • 103 + 2 • 102 + 5 • 101 + 7 • 100 = 8000 + 200 + 50 + 7 (Пример записан и разобран на доске)
Таким образом, с продвижением от цифры к цифре справа налево «вес» каждой цифры увеличивается в 10 раз. Это связано с тем, что основание системы счисления равно десяти.
Перевод двоичных чисел в десятичную систему.
А вот пример многозначного двоичного числа:
1101012.
Двойка внизу справа указывает на основание системы счисления. Это нужно для того, чтобы не перепутать двоичное число с десятичным. Ведь существует же десятичное число 110101! Вес каждой следующей цифры в двоичном числе при продвижении справа налево возрастает в 2 раза. Развернутая форма записи данного двоичного числа выглядит так:
1101012 = 1 • 25 + 1 • 24 + 0 • 23 + 1 • 22 + 0 • 21 + 1 • 20 = 5310 (Пример записан и разобран на доске)
Таким способом мы перевели двоичное число в десятичную систему.
Переведем в десятичную систему еще несколько двоичных чисел.
102 =21 =2; 1002 =22 =4; 10002 =23 =8; 100002 = 24 = 16; 1000002 = 25 = 32 ( учащиеся выполняют самостоятельно в тетради)
Таким образом, получилось, что двузначному десятичному числу соответствует шестизначное двоичное! И это характерно для двоичной системы: быстрый рост количества цифр с увеличением значения числа.
Вот как выглядит начало натурального ряда чисел в десятичной (А10) и двоичной (А2) системах счисления:
| A10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A2 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
| A10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| А2 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 | 10011 | 10100 |
Перевод десятичных чисел в двоичную систему.
Существует процедура, позволяющая легко выполнить перевод десятичного числа в двоичную систему. Она состоит в том, что данное десятичное число делится на 2. Полученный остаток — это младший разряд искомого числа. Полученное частное снова делится на 2, полученный при этом остаток — это следующий разряд искомого числа. Так продолжается до тех пор, пока частное не станет меньше двойки (основания системы). Это частное — старшая цифра искомого числа.
Существуют два способа записи деления на 2. Продемонстрируем это на примере перевода числа 37 в двоичную систему (Пример записан и разобран на доске)
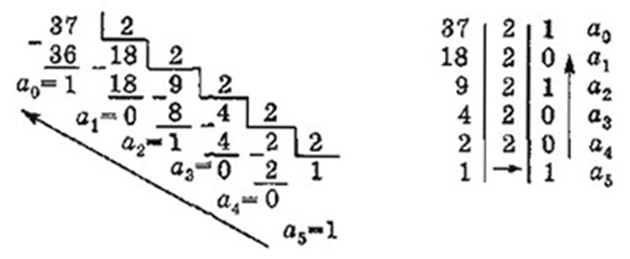
Здесь а5, а4, а3, а2, а1, а0 — обозначения цифр в записи двоичного числа по порядку слева направо. В результате перевода получим: 3710 = 1001012.
Закрепление материала. Работа у доски.
У: У вас на столах лежат карточки с заданиями. Начинаем выполнять с первого задания. Желающие поработать у доски?

Какие двоичные числа соответствуют следующим десятичным числам: 128; 256; 512; 1024?
Чему в десятичной системе равны следующие двоичные числа: 1000001; 10000001; 100000001; 1000000001?
Переведите в десятичную систему следующие двоичные числа: 101; 11101; 101010; 100011; 10110111011.
Переведите в двоичную систему счисления следующие десятичные числа: 2; 7; 17; 68; 315; 765; 2047.
Итоги урока.
У: Ребята, какова была цель нашего урока-электива?
у: Познакомиться с понятием «система счисления», научиться переводить числа из двоичной системы в десятичную и наоборот.
У: Совершенно верно! Молодцы! Наша цель достигнута.
У: Все молодцы, вы сегодня хорошо поработали! Спасибо за урок!
Дача домашнего задания.
У: Прочитайте лист с теорией и решите задания с карточки, которые не успели выполнить на уроке.
Конспек урока-электива
ТЕМА: «Десятичная и двоичная системы счисления».


















