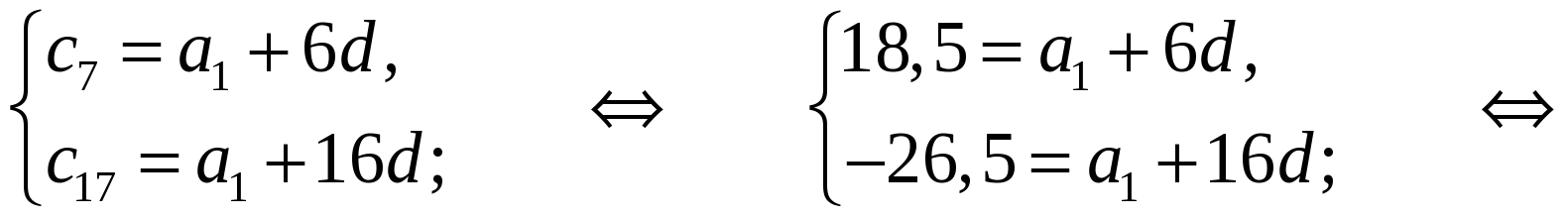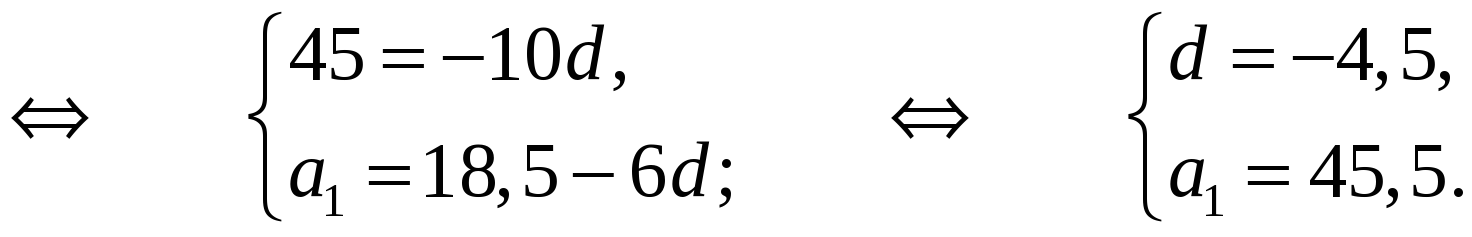Формула суммы первых n членов арифметической прогрессии.
Цели: 1. закреплять умения и навыки применения формулы суммы первых п членов арифметической прогрессии при решении задач;
2. коррекция логического мышления, коррекция развития речи.
3. повышение мотивации к учению.
Ход урока.
Организационный момент. Работа за экраном. Фонетическая разминка:
а.и.м.т.ч.ск.я пр.гр.сс..
п.сл.д.в.т.льн.с.ь
р.з.о..ь
а.г.б..
н.т.р.л.н.е ч..л.
II. Устная работа.
1. Является ли арифметической прогрессией последовательность, заданная формулой:
хп = 2п + 1;
уп = п2 – п;
zn = –64?
2. Найдите разность арифметической прогрессии:
17; 13; 9; …
3. (ап) – арифметическая прогрессия, вычислите:
а7, если а1 = 1, d = –2;
III. Проверочная работа.
В а р и а н т 1
1) Найдите сумму первых двенадцати членов арифметической прогрессии, если а1 = 16,5; d = –1,5.
2) Найдите сумму первых сорока членов последовательности, заданной формулой ап = 3п + 2.
В а р и а н т 2
1) Найдите сумму первых десяти членов арифметической прогрессии, если а1 = 18,5; d = –2,5.
2) Найдите сумму первых двадцати членов последовательности, заданной формулой хп = 4п + 5.
О т в е т ы:
| Задание | I вариант | II вариант |
| 1 | 99 | 72,5 |
| 2 | 2540 | 940 |
Физкультминутка.
IV. Формирование умений и навыков.
Все упражнения, решаемые на этом уроке, можно условно разделить на следующие виды:
1) На вычисление суммы первых п членов арифметической прогрессии по двум формулам (требует выбора формулы в зависимости от условия задачи).
2) На вычисление отдельных членов, числа членов, разности арифметической прогрессии по формулам суммы первых п членов.
3) На нахождение вышеперечисленных величин при наличии дополнительных условий и ограничений, сводящиеся к решению систем уравнений, неравенств.
Задания первого вида были выполнены в ходе проверочной работы.
Упражнения:№ 610, № 612. Решение у доски с комментариями.
Р е ш е н и е
№ 610.
В этом упражнении задана арифметическая прогрессия (ап), где
а1 = 10; d = 3. Наши формулы позволяют находить сумму с первого по п-й член включительно, а требуется найти с 15-го по 30-й включительно. Заметим, что мы можем найти суммы членов арифметической прогрессии с 1-го по 30-й и с 1-го по 14-й включительно, их разность и даст искомый результат.
S30 = 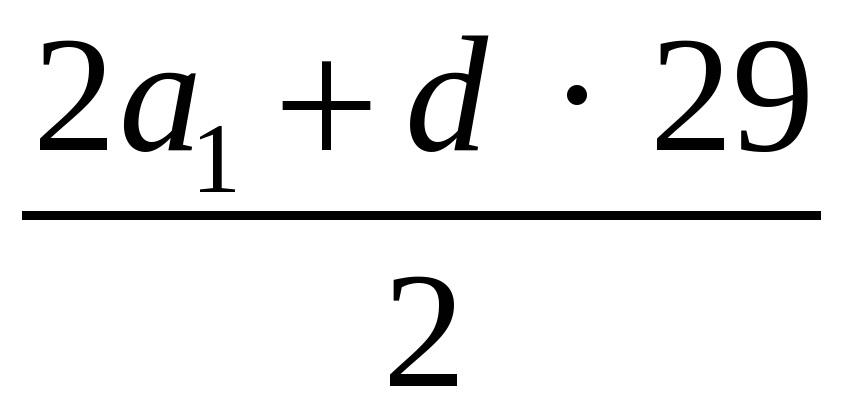 · 30; S30 =
· 30; S30 = 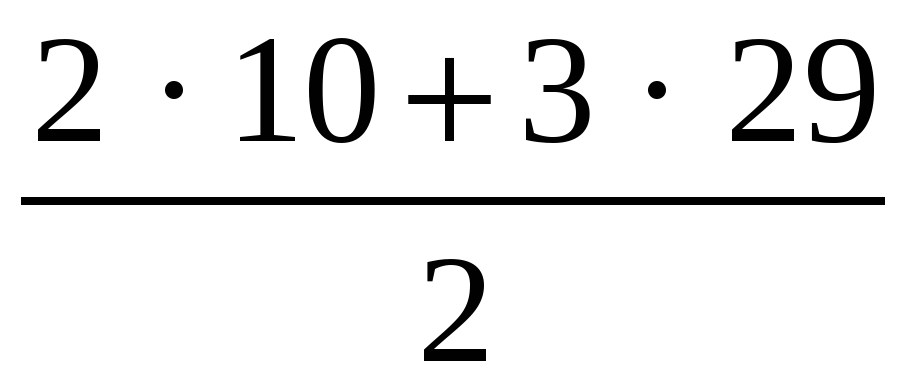 · 30 = 1605.
· 30 = 1605.
S14 = 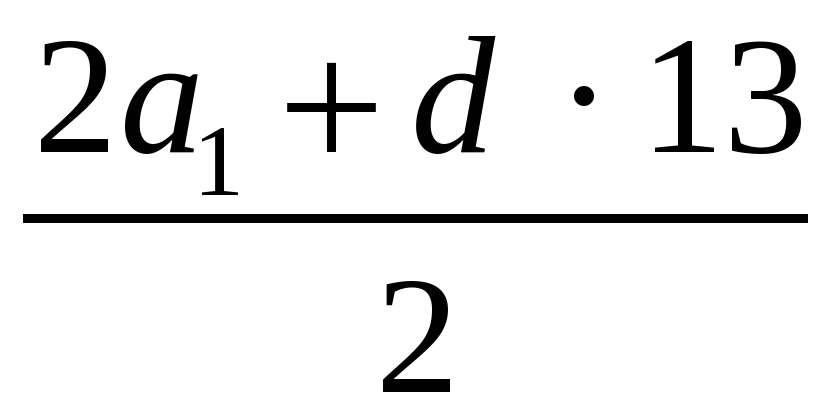 · 14; S14 =
· 14; S14 = 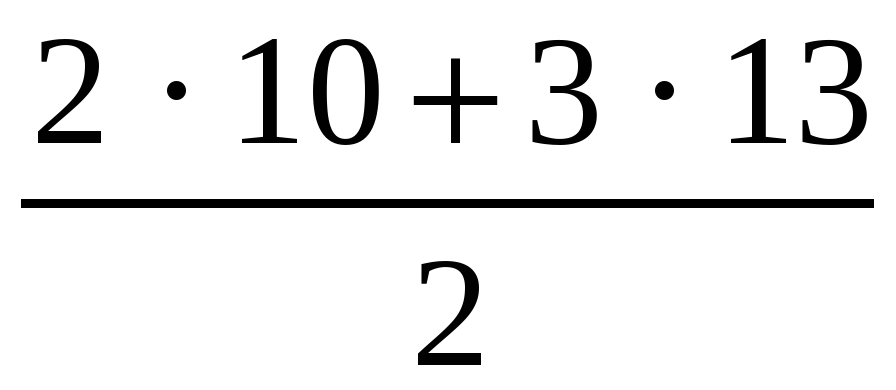 · 14 = 413.
· 14 = 413.
S30 – S14 = 1192.
О т в е т: 1192.
№ 612.
(сп) – арифметическая прогрессия;
с7 = 18,5; с17 = –26,5.
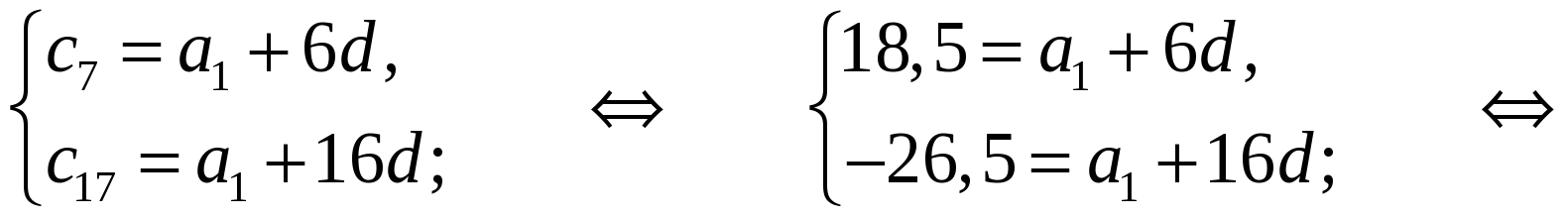
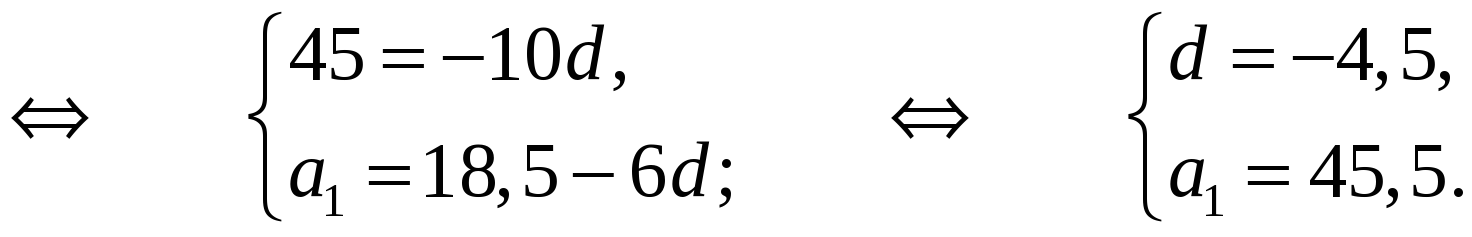
S20 = 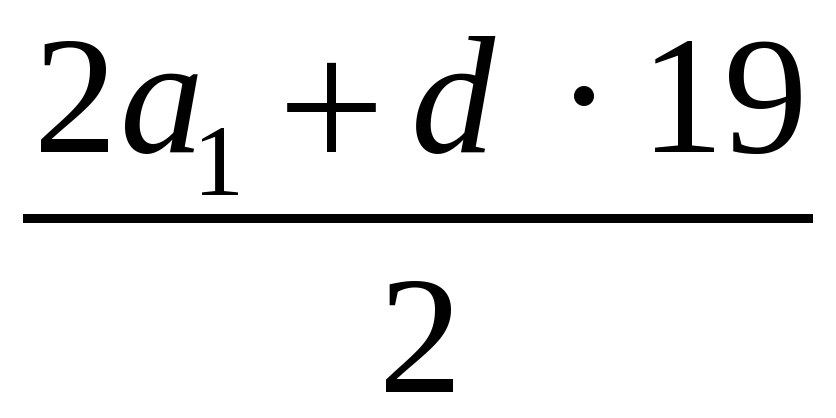 · 20; S20 =
· 20; S20 = 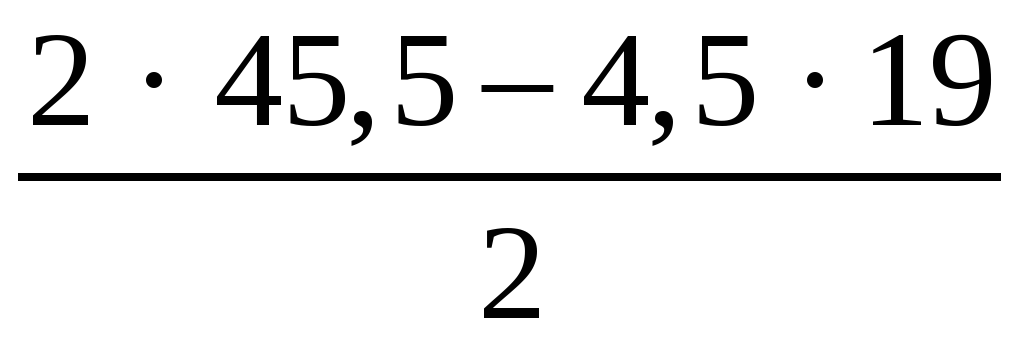 · 20 = 55.
· 20 = 55.
О т в е т: 55.
V. Итоги урока.
Домашнее задание: № 611, № 613.
а.и.м.т.ч.ск.я пр.гр.сс..
п.сл.д.в.т.льн.с.ь
р.з.о..ь
а.г.б..
н.т.р.л.н.е ч..л.
1. Является ли арифметической прогрессией последовательность, заданная формулой:
хп = 2п + 1;
уп = п2 – п;
zn = –64?
2. Найдите разность арифметической прогрессии:
17; 13; 9; …
3. (ап) – арифметическая прогрессия, вычислите:
а7, если а1 = 1, d = –2;
В а р и а н т 1
1) Найдите сумму первых двенадцати членов арифметической прогрессии, если а1 = 16,5; d = –1,5.
2) Найдите сумму первых сорока членов последовательности, заданной формулой ап = 3п + 2.
В а р и а н т 1
1) Найдите сумму первых двенадцати членов арифметической прогрессии, если а1 = 16,5; d = –1,5.
2) Найдите сумму первых сорока членов последовательности, заданной формулой ап = 3п + 2.
В а р и а н т 1
1) Найдите сумму первых двенадцати членов арифметической прогрессии, если а1 = 16,5; d = –1,5.
2) Найдите сумму первых сорока членов последовательности, заданной формулой ап = 3п + 2.
В а р и а н т 2
1) Найдите сумму первых десяти членов арифметической прогрессии, если а1 = 18,5; d = –2,5.
2) Найдите сумму первых двадцати членов последовательности, заданной формулой хп = 4п + 5.
В а р и а н т 2
1) Найдите сумму первых десяти членов арифметической прогрессии, если а1 = 18,5; d = –2,5.
2) Найдите сумму первых двадцати членов последовательности, заданной формулой хп = 4п + 5.
В а р и а н т 2
1) Найдите сумму первых десяти членов арифметической прогрессии, если а1 = 18,5; d = –2,5.
2) Найдите сумму первых двадцати членов последовательности, заданной формулой хп = 4п + 5.
| Задание | I вариант | II вариант |
| 1 | 99 | 72,5 |
| 2 | 2540 | 940 |
1. Является ли арифметической прогрессией последовательность, заданная формулой:
хп = 2п + 1;
уп = п2 – п;
zn = –64?
2. Найдите разность арифметической прогрессии:
17; 13; 9; …
3. (ап) – арифметическая прогрессия, вычислите:.
а7, если а1 = 1,
d = –2;