Конспект урока "Числовые последовательности"

У р о к 3

Название предмета Алгебра

Класс 9

УМК Мордкович А.Г. Алгебра. 9 кл.: В 2 ч. Ч.1: Учебник для общеобразоват. учреждений/ А.Г.Мордкович. - 10-е изд,стер.–М.: Мнемозина, 2010. – 215 с.: ил.

Мордкович А.Г. и др. Алгебра. 9 кл.: В 2 ч. Ч.2: Задачник для общеобразоват. учреждений/(А.Г.Мордкович и др.);под ред. А.Г.Мордковича. - 10-е изд., стер. –М.: Мнемозина, 2010. – 255 с.: ил

Уровень обучения базовый

Тема урока «Числовые последовательности»

Общее количество часов, отведенное на изучение темы 16

Место урока в системе уроков по теме №3

Цель урока закрепить знание учащимися способов задания числовой последовательности; изучить свойства числовых последовательностей и научить применять их в ходе выполнения упражнений; развивать логическое мышление учащихся

Задачи урока

Образовательные:

• проверить умение записывать последовательности

• актуализировать знания учащихся о последовательностях

• научить распознавать способы задания последовательности, виды последовательностей,свойства числовых последовательностей

;

Развивающие:

• развивать логическое мышление;

• развивать математическую речь учащихся, эстетику письма ;

• развивать наблюдательность, память учащихся.

Воспитательные:

• прививать усидчивость, аккуратность выполнения ЗАПИСЕЙ

• формирование стремления вести здоровый образ жизни и заниматься спортом;

• формировать положительное отношение к предмету и интерес к знаниям.

: создать условия для формирования коммуникативной компетенции;

создать условия для умения анализировать, сравнивать делать выводы, выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности

создать условия для работы с понятиями и умения обрабатывать информацию.

уметь в процессе реальной ситуации использовать ПОНЯТИЕ ПОСЛЕДОВАТЕЛЬНОСТИ. , свойства числовых последовательностей

умение работать в парах, слушать собеседника и вести диалог, выражать и аргументировать свою точку зрения;

уметь обрабатывать информацию; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности.

Техническое обеспечение: компьютер ,мультимедийный проектор

Содержание урока

1. Организационный момент.

2. Актуализация знаний.

3. Изучение нового материала

4. Закрепление.

5. Проверка усвоения темы.

6. Задание на дом.

.

Ход урока

1 Организационный момент

.2 Актуализация знаний.

1. Назовите способы задания числовой последовательности и опишите каждый из способов.

2. Приведите примеры числовой последовательности, заданной:

а) формулой n-го члена;

б) словесно;

в) рекуррентный формулой. Это № 15.5.

3. Решить устно № 15.3 и № 15.4 (а; г).

4. Решить устно № 15.7.

х_n = 7  n; х₁ = 7; х₂ = 14; х₃ = 21; х₄ = 28.

х₈ = 56; х₁₀ = 70; х₃₇ = 7  37 = 259.

II. Изучение нового материала.

1. Числовая последовательность – частный случай числовой функции, а потому некоторые свойства функций рассматривают и для последовательностей. Ограничимся свойством монотонности.

1. О п р е д е л е н и е 2. Последовательность (y_n) называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y₁ y₂ y₃ y₄ y_n y_{n + 1}

3. Рассмотреть решение примеров 14 и 17 на с. 155 учебника.

4. О п р е д е л е н и е 3. Последовательность (y_n) называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y₁ y₂ y₃ y₄ … y_n y_{n + 1} …

5. Рассмотреть решение примеров 15 и 18 учебника на с. 155.

6. Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

7. Разобрать решение примера 16 на с. 145 учебника.

8. Записать в тетрадях вывод:

1) Если а 1, то последовательность у_n = aⁿ возрастает.

2) Если 0 a у_n = aⁿ убывает.

.4. Закрепление.

1. Решить № 15.24 на доске и в тетрадях.

Простые числа: 2; 3; 5; 7; 11; 13; 17.

Квадраты простых числе: 4; 9; 25; 49; 121; 169; 289.

2. Решить № 15.22 (а; в).

а) y_n = 3n + 4;

у₁ = 3  1 + 4 = 7;

у₂ = 3  2 + 4 = 10;

у₃ = 3  3 + 4 = 13;

у₄ = 3  4 + 4 = 16;

у₅ = 19.

Имеем 7; 10; 13; 16; 19… возрастающая последовательность.

в) y_n = 7n – 2;

у₁ = 7  1 – 2 = 5;

у₂ = 7  2 – 2 = 12;

у₃ = 7  3 – 2 = 19;

у₄ = 26, …

Получим 5; 12; 19; 26; 33… возрастающая.

3. Решить № 15.23 (а; в) самостоятельно с проверкой.

а) y_n = –2n – 3; у₁ = –5; у₂ = –7; у₃ = –9; у₄ = –11…

значит, –5; –7; –9; –11; –13; … убывающая.

в) y_n = 4 – 5n; у₁ = –1; у₂ = –6; у₃ = –11; у₄ = –16…

Имеем, –1; –6; –11; –16; … убывающая.

4. Решить № 15.35 (в; г).

Учитель объясняет решение.

№ 15.35 (в), задание № 15.35 (г) решают самостоятельно.

в)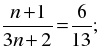

13(n + 1) = 6(3n + 2);

13n + 13 = 18n + 12;

5n = 1;

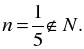
О т в е т: не существует.

г)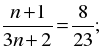

23(n + 1) = 8(3n + 2);

23n + 23 = 24n + 16;

n = 7.

О т в е т: 7.

5.Проверка усвоения темы

5. Решить № 15.41 (а) и № 15.42 (а) устно.

6. Решить № 15.36 (в; г) на доске и в тетрадях.

в) (2n – 1)(3n + 2) = 153;

6n² + n – 155 = 0;

D = 3721 = 61²;

n₁ = 5; n₂ = 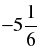не удовлетворяет.

О т в е т: является n = 5.

г) (2n – 1)(3n + 2) = –2;

6n² + n = 0;

n(6n + 1) = 0;

n = 0 или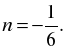

Эти значения n не натуральные числа.

О т в е т: нет.

7. Решить № 15.37 (в; г) с комментированием на месте.

О т в е т: в) x_n = 15 – 4n; г)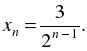

6. Итог урока.

Домашнее задание: на отдельных листочках решить из домашней контрольной работы № 4 на с. 118–119 № 1, № 2 и № 3; к ним добавить по вариантам № 15.35 (а; б); № 15.36 (а; б); № 15.37 (а; б). 1 ВАРИАНТ а): 2 ВАРИАНТ Б)