Конспект урока "Определение производной" 10 класс

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №10 г. Ногинска Московской области

«Определение производной»

Конспект урока по алгебре и началам математического анализа

в 10 классе

Автор Лукахина Марина Юрьевна

Ногинск 2013 г.

Цели урока:

1. Сформировать представление о производной как математической модели различных ситуаций из разных областей деятельности.

2. Научить видеть приложения производной на геометрических иллюстрациях.

3. Создать условия для развития логического мышления, расширения кругозора учащихся.

4. Создать условия для развития коммуникативных качеств.

Задачи урока:

1. Познакомить учащихся с понятием производной.

2. Показать применение новой математической модели при решении различных задач.

3. Вывести формулы дифференцирования с помощью алгоритма.

Этапы урока:

1. Организационный этап

Часто бывает так, что решая задачи, на первый взгляд, разные по содержанию, мы приходим к одной и той же математической модели. Вы уже знакомы с различными математическими моделями – уравнениями, неравенствами, системами уравнений и неравенств и другими. Сегодня вы познакомитесь с абсолютно новой для вас моделью, которая в дальнейшем поможет нам решать самые разнообразные задачи.

1. Этап подготовки к усвоению нового материала

Слайды 3-5.

1. Устные упражнения с коллективным обсуждением. Найдите тангенс угла наклона прямой к положительному направлению оси абсцисс и угловой коэффициент этой прямой.

2. Что такое приращение функции, приращение аргумента?

1. Этап усвоения новых знаний

Рассмотрим две различные задачи – физическую и геометрическую, процесс решения которых как раз и приводит к возникновению новой математической модели.

Слайд 7.

Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s = s(t), где t – время (в секундах), s(t) – положение тела на прямой (т.е. координата движущейся материальной точки) в момент времени t. Найти скорость движения тела в момент времени t (в м/с).

Решение. Пусть в момент времени t тело находилось в точке М, тогда чему равно ОМ? (ОМ = s(t)). Дадим аргументу t приращение Δt и рассмотрим ситуацию в момент времени t + Δt. Координата тела изменилась, оно теперь находится в точке Р, ОР = ? (ОР = s(t + Δt)).

МР = ? (ОР – ОМ = s(t + Δt) - s(t) = Δs). Как найти среднюю скорость тела на промежутке МР? (v_ср = Δs/Δt). Чтобы найти мгновенную скорость, надо, чтобы Δt→0, т.е.

Слайд 8.

Прежде чем перейти ко второй задаче, выясним, что понимать под касательной к кривой. Пусть на графике некоторой функции зафиксирована точка М. Возьмем рядом с ней на этом графике точку Р. Построим прямую МР – секущую. Будем приближать точку Р к точке М до тех пор, пока точка Р не совместится с точкой М. Полученная прямая – касательная – предельное положение секущей.

Слайд 9.

Задача 2 ( о касательной к графику функции).

Дан график функции у = f(x). На нем зафиксирована точка М с координатами (а; f(а)). Найти угловой коэффициент касательной к графику функции, которая построена через точку М.

Решение. Дадим аргументу а приращение Δх и рассмотрим точку Р(а + Δх; f(а + Δх)). Чему равен угловой коэффициент секущей? (Δу/Δх). При Δх→0 Р→М, получим касательную как предельное положение секущей МР и k_кас = lim k_сек при Δх→0, т.е.

Таким образом, две различные задачи привели к одной и той же математической модели - пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Многие задачи физики, химии, экономики и т.д. приводят в процессе решения к такой же модели. Значит, эту математическую модель надо изучить, т.е.:

а) дать ее формальное определение и присвоить ей новый термин;

б) ввести для нее обозначение;

в) исследовать свойства новой модели.

Слайды 10-11.

Определение. Пусть функция у = f(x) определена в некотором интервале, содержащем внутри себя точку х₀. Дадим аргументу приращение Δх такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции Δу (при переходе от точки х₀ к точке х₀ + Δх) и составим отношение Δу/Δх. Если существует предел этого отношения при Δх→0, то указанный предел называют производной функции у = f(x) в точке х₀ и обозначают f’(x₀).

Рассмотренные задачи 1 и 2 позволяют истолковать производную с физической и геометрической точек зрения.

Слайд 12.

Физический смысл производной.

Если s = s(t) – закон прямолинейного движения тела, то производная выражает мгновенную скорость, в момент времени t: v(t) = s’(t).

На практике во многих отраслях науки используется обобщение полученного равенства: если некоторый процесс протекает по закону s = s(t), то производная s’(t) выражает скорость протекания процесса в момент времени t.

Слайд 13.

Геометрический смысл производной.

Если к графику функции у = f(x) в точке с абсциссой х = а можно провести касательную, непараллельную оси у, то f’(а) выражает угловой коэффициент касательной, который равен тангенсу угла наклона к положительному направлению оси х.

Слайд 14.

В определении производной заложен алгоритм ее нахождения.

1. Зафиксировать значение х, найти f(x).

2. Дать аргументу приращение Δх, перейти в новую точку х + Δх, найти f(x + Δх).

3. Найти приращение функции Δу = f(x + Δх) - f(x).

4. Составить отношение Δу/Δх

5. Вычислить

Этот предел и есть f’(x).

1. Этап закрепления

1. Слайды 15-18.

Рассмотрим примеры применения новой модели к решению задач (ЕГЭ 3000 задач по математике).

1. Работа в группах (по 4 человека) по карточкам.

Задание 1.

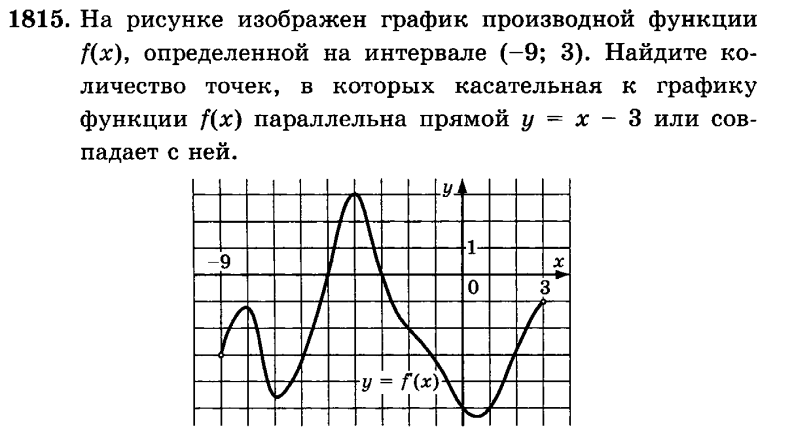
Коллективное обсуждение решений.

Задание 2.

С помощью алгоритма найти производные функций:

у = С, у = х, у = kx + m, у = х², у = 1/х, у = √х.

Слайд 19 Проверка результатов.

1. Подведение итогов урока

С каким новым понятием вы сегодня познакомились?

Какие задачи помогли нам увидеть новую математическую модель?

Какие задачи вы научились решать с помощью производной?

Какие формулы вывели?

У новой математической модели, с которой вы сегодня работали еще много пока неизвестных вам свойств. С ними мы будем работать на следующих уроках.

1. Задание на дом

§27. №27.4, №27.5, №27.12, №27.13, №27.14.

Информационные источники:

1. Учебник Алгебра и начала математического анализа 10 – 11 классы, Мордкович А.Г., М.: Мнемозина 2009

2. Методическое пособие для учителя Алгебра и начала математического анализа 10 – 11 классы, Мордкович А.Г., М.: Мнемозина 2009

3. ЕГЭ 3000 задач с ответами по математике, под редакцией А. Л. Семенова и И. В. Ященко, М.: Экзамен 2012

4. ЕГЭ 3000 задач с ответами по математике, под редакцией А. Л. Семенова и И. В. Ященко, электронная версия nashol.com