Тема « Решение треугольника.»
Цели урока:
1 . Закрепление и углубление знаний учащихся о теоремах синусов и косинусов и их применение к решению треугольников, а также их соотношение между углами треугольника и противоположными сторонами.
2. Развитие активности учащихся, формирование учебно-познавательных действий, коммуникативных навыков, умение анализировать и устанавливать связь между элементами темы. показать связь теории с практикой, способствовать выработке навыков решения задач, применяя раннее изученный материал.
3. Воспитывать ответственное отношение к учебному труду.
Воспитывать способность к самоанализу, рефлексии.
Оборудование: презентация, проектор, таблица Брадиса, лист самоконтроля.
ХОД УРОКА
Организационный момент. ( сообщение темы и целей урока)
У каждого человека должна быть своя высота
От исходной точки до вершины
И должна быть своя мечта
Высота с мечтой неразделимы.
Мотивация урока.
Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но возвысите свою душу».
Давайте делиться своими идеями, которые придут вам в голову, и не бойтесь ошибиться, любая мысль может дать нам новое направление поиска. Пусть наши достижения и не покажутся кому-то крупными, но ведь это будут наши собственные достижения!
Актуализация опорных знаний.
«Истина – ложь» ( на предложенные высказывания учащиеся показывают ту карточку с буквой которую считают верной «И» - истина, «Л» - ложь)
Треугольник это геометрическая фигура имеющая 3 стороны и 3 угла (И)
Каждая сторона треугольника равна сумме двух других сторон (Л)
В треугольнике против меньшего угла лежит большая сторона (Л)
Площадь треугольника равна произведению его стороны на высоту проведенную к этой стороне (И)
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними (Л)
Верно ли выражение для данного треугольника

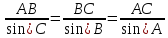 (Л)
(Л)
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе (И)
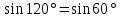 (И)
(И)
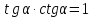 (И)
(И)
Решить треугольник значит найти угол и сторону этого треугольника. (Л)
( листе самоконтроля отметь на какой ступеньке вы оказались)
2 ступень
Давайте двигаться дальше и посмотрим сможем ли мы взобраться на следующую ступень.
Сегодня на уроке повторим как по данным длинам или градусным мерам трёх элементов треугольника вычислить остальные его элементы. Решая задачи такого типа, мы говорим …(решаем треугольник)
И прежде чем приступить к решению различных задач, нам необходимо вспомнить:
Какие теоремы применяются при решении треугольников?
Какие задачи при этом можно выделить? (по стороне и двум прилежащим к ней углам; по двум сторонам и углу между ними; по трём сторонам; по стороне, прилежащему к ней углу и стороне противолежащей данному углу)(Слайд таблица с формулами)

Решение задач на повторение.
Решение задач в группах по уровням. ( с последующей проверкой и комментарием)
Задача: В треугольнике АВС АВ=0,6см, ВС=0,5см, 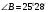 .Найдите сторону АС.
.Найдите сторону АС.
Решение
Воспользуемся теоремой косинусов
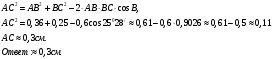
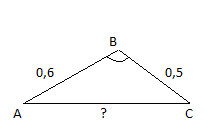
3 группа: уровень А
Задача: В треугольнике АВС АВ=10см, 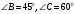 . Найдите сторону АС.
. Найдите сторону АС.
Решение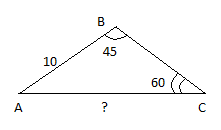
Воспользуемся теоремой синусов:
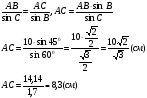
 Ответ:8,3 см
Ответ:8,3 см
ИСТОРИЧЕСКАЯ СПРАВКА
Тригонометрия- «измерение треугольников» - развивалась, прежде всего в связи с потребностями астрономии, географии, навигации. Поэтому её зачатки были в Древнем Вавилоне, где астрономия получила значительное развитие. Синус и косинус появляются в астрономических сочинениях индийских ученных 9-10вв.
Тангенс появился в связи с задачей определения высоты Солнца по длине тени, решение которой необходимо для изготовления солнечных часов. Выделение тригонометрии в специальный раздел математики связано с именем выдающегося персидского ученого Н а с и р э д д и н а Т у с и (1201-1274). В Европе первое изложение тригонометрии было дано в 15в. немецким ученым Р е г и о м о н т а н о м ( 1436-1476). Современный вид тригонометрия получила в трудах крупнейшего математика 18в. Леонарда Э й л е р а (1707-1783).
Теорему косинусов знали еще древние греки, ее доказательство содержится во 2 книге «Начал» Евклида как обобщенная теорема Пифагора. Нить практической геометрии тянулась от вавилонян и древних египтян через Герона вплоть до новых времён. В этот период появляется много руководств по геометрии, в которых излагаются правила, формулы и рецепты для решения тех или иных практических задач.
V. Решение задач с практическим содержанием.
Решение задач в парах ( 3 варианта)
1 группа:
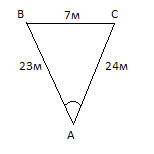
Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и стоек ворот. Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м.
Решение:
Решим треугольник АВС(задача 1) и найдем угол А, равный α
По теореме косинусов определим cos А
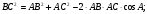
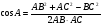
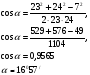
Ответ: 16057/
2 группа: задача №1036(учебник «Геометрия 7-9», Атанасян Л.С.)
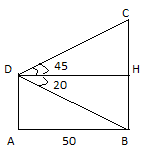
Наблюдатель находится на расстоянии 50 м от башни, высоту которой хочет определить.
Основание башни он видит под углом 2° к горизонту, а вершину — под углом 45° к горизонту.
Какова высота башни?
Дано: АВ=50 м, BDH=20, CDH=450, DH||AB.
Найти: СВ
Решение
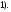 DH || AB →
DH || AB →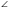 BDH=
BDH=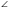 DBA=20, как накрест лежащие.
DBA=20, как накрест лежащие.
cos 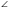 DBA=
DBA=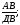 ДВ=
ДВ=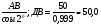
Применим терему синусов:
ΔСDB: 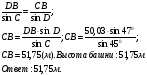
ЭКЗАМЕН НЕ ЗА ГОРАМИ
Задания учащимся с планом решения ( подготовка к ГИА).
Задача 1.
Две стороны треугольника имеют длины 6см и 12 см, а угол между ними равен 1200. Найдите длину биссектрисы, проведенной к большей стороне.
Решение
Пусть дан треугольник АВС:АВ=6 см, ВС=12 см, 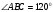 .Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем:
.Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем:
 cos 1200=
cos 1200=
36 + 144 - 2 6
6 12
12 (-0,5) = 252; AC =
(-0,5) = 252; AC =  (см)
(см)
Сегодня мы решили несколько задач на нахождения неизвестных сторон треугольника, вывели новую формулу для нахождения высоты треугольника, попробовали свои силы для определения расстояния до недоступного примета, применив изученные способы решения. И мы попробовали свои силы, оценили свои знания, свои возможности. Ведь «самое трудное – познать самого себя»(Фалес)
VII. Подведение итогов.
Рефлексия
Ребята, что узнали на уроке нового, как работал каждый из вас. Где на уроке почувствовали неуверенность, что показалось сложным. Ребята предлагаю сейчас каждому из вас высказаться одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я приобрел…
я научился…
у меня получилось …
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Дополнительно
Сильным учащимся можно предложить сделать индивидуальные задания у доски или на парте.
Карточка 1: Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o - с другой. Найти длину скатов крыши с точностью до сантиметра.
Решение
1)Угол крыши
2)По теореме синусов
3)По теореме синусов:
Ответ: 5,912 см; 6,762 м.
Домашнее задание № 1037








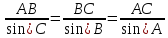 (Л)
(Л)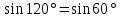 (И)
(И)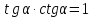 (И)
(И)
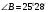 .Найдите сторону АС.
.Найдите сторону АС. 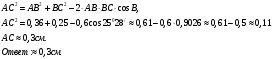

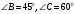 . Найдите сторону АС.
. Найдите сторону АС. 
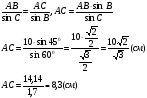
 Ответ:8,3 см
Ответ:8,3 см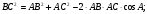

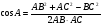
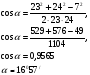

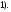 DH || AB →
DH || AB →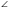 BDH=
BDH=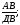 ДВ=
ДВ=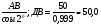
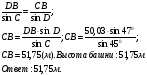
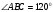 .Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем:
.Сторона АС-наибольшая, так как она лежит против тупого угла. По теореме косинусов имеем:

















