Контрольная работа "Последовательности"

Контрольная работа

Последовательности

Вариант 1

Задание 1

а) Укажите разность арифметической прогрессии – 2; 2; 6;10;…

б) Найдите четвертый член геометрической прогрессии: 3; 1; ;…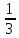

Задание 2

В первый день магазин продал 18 кг муки, а в каждый следующий продавал на 3 кг муки больше, чем в предыдущий. Найдите, сколько муки продал магазин за пять дней.

Задание 3

а) Найдите сумму пяти первых членов геометрической прогрессии (с_n), если с₁= 0,4; а с₂= 1,2.

б) Найдите номер члена арифметической прогрессии, равного -2,94, если а₁ = 1,26, а d= - 0,3.

Задание 4

а) Найдите сумму всех положительных членов арифметической прогрессии 55; 51; …

б) Найдите сумму всех трехзначных чисел, которые при делении на 23 дают остаток 17.

Задание 5

Найдите, при каком значении переменной а числа а+8, а+2, 3а-2 будут последовательными членами геометрической прогрессии. Найдите эти числа.

ИЛИ

Найдите четыре числа, первые три из которых составляют возрастающую геометрическую прогрессию, а последние три – арифметическую прогрессию, если сумма крайних чисел равна 32, а сумма средних чисел равна 24.

Контрольная работа

Последовательности

Вариант 2

Задание 1

а) Укажите разность арифметической прогрессии – 3; 3; 9;15;…

б) Найдите четвертый член геометрической прогрессии: 2; 1; ;…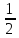

Задание 2

В первый день магазин продал 12 кг сахара, а в каждый следующий продавал на 2 кг сахара больше, чем в предыдущий. Найдите, сколько сахара продал магазин за шесть дней.

Задание 3

а) Найдите сумму первых шести членов геометрической прогрессии (с_n), если с₁= - 0,3; а с₂= - 0,6.

б) Найдите номер члена арифметической прогрессии, равного -9,7, если а₁ = -3,7, а d= - 0,6.

Задание 4

а) Найдите сумму всех отрицательных членов арифметической прогрессии -63; -58; …

б) Найдите сумму всех трехзначных чисел, которые при делении на 29 дают остаток 13.

Задание 5

Найдите, при каком значении переменной а числа 3а+1, а+5, а-7 будут последовательными членами геометрической прогрессии. Найдите эти числа.

ИЛИ

Найдите четыре числа, первые три из которых составляют убывающую арифметическую прогрессию, а последние три – геометрическую прогрессию, если сумма крайних чисел равна 7, а сумма средних чисел равна 6.
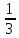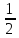