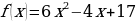МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ
СВЕРДЛОВСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СВЕРДЛОВСКОЙ ОБЛАСТИ
«ПЕРВОУРАЛЬСКИЙ ПОЛИТЕХНИКУМ»
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
для проведения промежуточной аттестации
по учебной дисциплине
ОУД. 04 Математика
по программе подготовки
08.01.07 Мастер общестроительных работ
форма проведения оценочной процедуры
экзамен
| РАССМОТРЕНО цикловой комиссией (ЦК) Председатель ЦК ____________ Шаяхметова Л.Х. Протокол заседания ЦК от «___»___________ 2023 г. № ____
| Разработчик: Мордашкина А,Ю.,преподаватель, 1 квалификационная категория |
Первоуральск
2023
Пояснительная записка
Настоящий комплект контрольно-измерительных материалов предназначен
для проведения завершающей аттестации по общеобразовательной учебной дисциплине ОДБ.03 «Математика» по подготовке квалифицированных рабочих и служащих в 2023-2024 учебном году по ОП 08.01.07 Мастер общестроительных работ
Комплект состоит из 2 вариантов и рассчитан на одну учебную группу. В каждом билете содержится 15 заданий разного уровня сложности по шести основным разделам курса математики, изученным в данном семестре:
показательная функция,
логарифмическая функция,
тригонометрические функции
производная, ее применение
интеграл и его применение
геометрия
В каждом разделе предложено три задания разного уровня сложности:
а – 0,5 балла – базовый уровень сложности
б – 1 балл – оптимальный уровень сложности
в – 1,5 балла – расширенный уровень сложности
Учащийся сам выбирает задания, не менее трех тем и уровень сложности заданий, которые будет выполнять.
Для учащихся критерий оценки дается в баллах, соответственно уровню сложности, указанной в билете:
Оценка «3» ставится, если учащийся выполнил задания «а» и «б» трех (или более) тем и набрал от2,5 до 4 баллов.
Оценка «4» ставится если учащийся выполнил задания «б» и «в» трех (или более) тем и набрал от 4 до 6 баллов.
Оценка «5» ставится если учащийся выполнил задания «б» и «в» трех (или более) тем и набрал более 6 баллов.
Верно (без ошибок и недочетов) выполненное задание оценивается указанным в билете количеством баллов. За допущенную грубую ошибку снимается 0,5 балла, за недочет снимается 0,2 балла.
Работа должна быть выполнена аккуратно, с требуемыми объяснениями и комментариями, с учетом требований к оформлению решений математических задач.
Уровень сформированности общих компетенций оценивается в соответствии с таблицей:
базовый уровень – 10 – 15 баллов
оптимальный уровень – 16 – 25 баллов
расширенный уровень – 26 баллов и более.
Оценка работы по уровням деятельности
| Уровни деятельности
| УУД | Обозначение задания в работе | Параметры и формы оценки | баллы |
| Эмоцион-психологические |
|
| Наблюдение за поведением и эмоциональной устойчивостью обучающихся во время экзамена |
|
| Регулятивный | Регулятивные |
| Верно оформлено решение | 1 |
| 1А, | Применены свойства степени Решено линейное уравнение | 1 1 |
| 2А, | Применено определение логарифма Решено линейное уравнение | 1 1 |
| 3А, | Применена формула корней уравнения | 1 |
| 4А, | Найдена производная Найдено значение производной в заданной точке | 1 1 |
| 5А, | Применена формула Ньютона-Лейбница Вычислено значение интеграла | 1 1 |
| 6А | Выбрана верная формула Найдена необходимая величина | 1 1 |
| Социальный | Коммуникативные | 4Б | Найдена производная функции и точки экстремума Найдены значения функции на концах отрезка и в точках экстремума Выбраны максимальное и минимальное значение функции | 1
1
1 |
| 5Б | Построена криволинейная трапеция Записан интеграл для вычисления площади фигуры Вычислен интеграл | 1 1 1 |
| 6Б | Сделан чертеж к задаче Выбрана формула для решения Найден ответ | 1 1 1 |
| Аналитический | Познавательные | 1Б | Выбран верный прием для решения Решено полученное уравнение Применено свойство степени | 1 1 1 |
| 2Б | Выбран верный прием для решения Решено полученное уравнение Решено логарифмическое уравнение | 1 1 1 |
| 3Б | Выполнены алгебраические преобразования Выбраны тригонометрические формулы Применены тригонометрические формулы | 1 1 1 |
| Творческий
| Личностные | 4В | Найдена производная Найдены точки экстремума Найдены промежутки возрастания и убывания функции Найдены значения функции Построен график функции | 1 1
1 1 1 |
| 5В | Построены все заданные линии Определена фигура Записана формула для вычисления площади Вычислена площадь фигуры | 1 1 1 1 |
| 6В | Записано условие задачи Сделан чертеж к задаче Найдена плоская фигура для нахождения элементов (промежуточной величины) Найдена необходимая величина | 1 1
1 1 |
| Самосовершенствования | Регулятивные | 1В, | Применен верный прием Найдены корни уравнения Учтено возрастание и убывание функции Решено неравенство | 1 1 1 1 |
| 2В | Применен верный прием Найдены корни уравнения Учтено возрастание и убывание функции Решено неравенство | 1 1 1 1 |
| 3В | Произведены необходимые преобразования для сведения к стандартному виду Выбран верный прием решения Выполнены тригонометрические преобразования Решено уравнение |
1 1 1 1 |
| Итого: |
|
| 56 |
| |
Инструкция для студентов.
Экзаменационная работа состоит из 2 билетов.
В каждом билете 15 заданий из шести основных разделов математики:
Показательная функция.
Логарифмическая функция.
Тригонометрические функции.
Производная и ее применение.
Интеграл и его применение.
Геометрия.
Каждый раздел содержит три задания разного уровня сложности, который указан слева от задания:
а – 0,5 балла – базовый уровень сложности
б – 1 балл – оптимальный уровень сложности
в – 1,5 балла – расширенный уровень сложности.
Вы сами выбираете задания, не менее трех тем и уровень сложности заданий, которые будете выполнять.
Критерии оценки соответствует уровню сложности задания, указанной в билете:
Оценка «3» ставится, если Вы выполнили задания «а» и «б» трех (или более) тем и набрали от2,5 до 4 баллов.
Оценка «4» ставится, если Вы выполнили задания «б» и «в» трех (или более) тем и набрали от 4 до 6 баллов.
Оценка «5» ставится, если Вы выполнили задания «б» и «в» трех (или более) тем и набрали более 6 баллов.
Верно (без ошибок и недочетов) выполненное задание оценивается указанным в билете количеством баллов. За допущенную грубую ошибку снимается 0,5 балла, за недочет снимается 0,2 балла.
Работа должна быть выполнена аккуратно, с необходимыми объяснениями и комментариями, с учетом требований к оформлению решений математических задач.
Экзамен 3 семестр.
1 вариант
3.1 Векторы в пространстве
а) Упростите выражение: 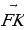 +
+ 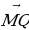 +
+ 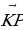 +
+ 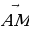 +
+ 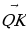 +
+ 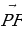
б) В параллелепипеде ABCDA1B1C1D1 диагонали грани DD1C1C пересекаются в точке M. Разложите вектор 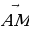 по векторам
по векторам 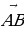 ,
, 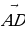 и
и 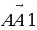
в) Дан параллелепипед ABCDA1B1C1D1. Укажите вектор  , начало и конец которого являются вершинами параллелепипеда, такой, что
, начало и конец которого являются вершинами параллелепипеда, такой, что 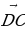 +
+ 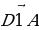 1 +
1 + 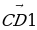 +
+  +
+ 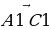 =
= 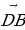
3.2 Координатный метод в пространстве
а) Даны векторы 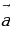 {-1;-2;0};
{-1;-2;0}; 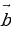 {0;-5;-2};
{0;-5;-2}; 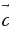 {2;1;-3}. Найдите координаты вектора
{2;1;-3}. Найдите координаты вектора 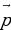 = 3
= 3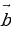 – 2
– 2 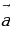 +
+ 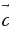
б) Даны векторы  = m
= m 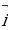 + 3
+ 3 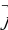 + 4
+ 4 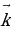 и
и 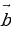 = 4
= 4 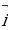 + m
+ m 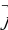 – 7
– 7 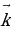 . При каком значении m векторы
. При каком значении m векторы 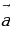 и
и 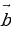 перпендикулярны?
перпендикулярны?
в) Вычислите периметр треугольника, вершинами которого являются точки A (1;-1;3); B (3;-1;1) и C (-1;1;3).
3.3 Производная
а) Вычислите значение производной функции f(x) = 3x4 – 2x2 + x – 18 в точке x0 = -1.
б) Составьте уравнение касательной к графику функции y = x - 3x2 + x в точке с абсциссой x0 = 2.
в) Тело, масса которого m = 5 кг, движется прямолинейно по закону S = 1 – t + t2 (где S измеряется в метрах, а t – в секундах). Найти кинетическую энергию тела 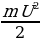 через 10 с после начала движения.
через 10 с после начала движения.
3.4 Применения производной
а) Найдите стационарные точки функции p(x) = x3 – 3x2 + 8.
б) Найдите наибольшее и наименьшее значение функции y = x4 – 8x2 + 5 на отрезке [-2;1].
в) Исследуйте функцию и постройте график: y = 3x5 – 5x3 + 1.
3.5 Цилиндр, конус, шар
а) Диаметр шара равен 8 см, найдите площадь его поверхности.
б) Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите площадь поверхности конуса.в) Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной от нее на 9 дм, равна 240 дм2. Найдите площадь поверхности цилиндра.
Экзамен 3 Семестр
2 вариант
3.1 Векторы в пространстве
А) Упростить выражение 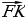 +
+ 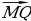 +
+ 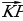 +
+ 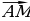 +
+ 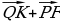
Б) Точка К – середина ребра B1C1 куба ABCDA1B1C1D1. Разложите вектор 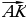 по векторам
по векторам 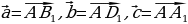
B) Дан параллелепипед ABCDA1B1C1D1 укажите вектор 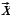 , начало и конец которого являются вершинами параллелепипеда, такой что
, начало и конец которого являются вершинами параллелепипеда, такой что 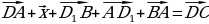 .
.
3.2 Координатный метод в пространстве.
А) Вычислите длину вектора 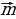 , заданного координатами
, заданного координатами 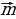
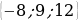
Б) Определите, какой угол между векторами 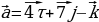 и
и 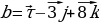 острый тупой или прямой?
острый тупой или прямой?
В) Компланарны ли векторы
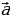
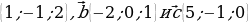
3.3 Производная.
А) Вычислите значение производной функции 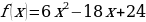 в точке
в точке 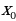 =5.
=5.
Б) Составьте уравнение касательной к графику функции 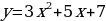 в точке.
в точке.
В) Определите ускорение тела движущегося по закону 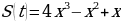 в момент времени
в момент времени 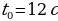 .
.
3.4 Применения производной.
А) Найдите стационарные точки функции 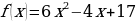
Б) Найдите масштабируемые и наименьшее значения функции y=2x3–3x2+12 на отрезке [-2;0].
В) Исследуйте функцию и постройте график y=x4–2x2+3
3.5 Цилиндр, конус, шар
А) Радиус основания цилиндра равен 3 см, а высота цилиндра 7 см. Вычислить площадь его поверхности.
Б) В шаре на расстоянии 3 см от центра проведено сечение, радиус которого равен 4 см. Вычислить площадь поверхности шара
В) Угол между образующей и осью конуса 6,5 см. Найдите площадь полной поверхности конуса
Оценочный лист экзамена по математике
группа:___________ ОП _________________________ дата проведения_____________________
| № | ФИ | Номер задания | баллы | оценка |
| 1А | 1Б | 1В | 2А | 2Б | 2В | 3А | 3Б | 3В | 4А | 4Б | 4В | 5А | 5Б | 5В | 6А | 6Б | 6В |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценочный лист экзамена по математике
группа:___________ ОП _________________________ дата проведения_____________________
| № | ФИ | Номер задания | баллы | оценка |
| 1А | 1Б | 1В | 2А | 2Б | 2В | 3А | 3Б | 3В | 4А | 4Б | 4В | 5А | 5Б | 5В | 6А | 6Б | 6В |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценочный лист экзамена по математике
группа:___________ ОП _________________________ дата проведения_____________________
| № | ФИ | Номер задания | баллы | оценка |
| 1А | 1Б | 1В | 2А | 2Б | 2В | 3А | 3Б | 3В | 4А | 4Б | 4В | 5А | 5Б | 5В | 6А | 6Б | 6В |
|
|
| 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|







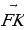 +
+ 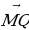 +
+ 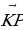 +
+ 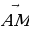 +
+ 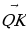 +
+ 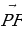
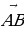 ,
, 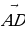 и
и 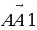
 , начало и конец которого являются вершинами параллелепипеда, такой, что
, начало и конец которого являются вершинами параллелепипеда, такой, что 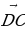 +
+ 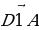 1 +
1 + 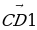 +
+ 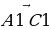 =
= 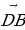
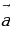 {-1;-2;0};
{-1;-2;0}; 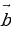 {0;-5;-2};
{0;-5;-2}; 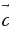 {2;1;-3}. Найдите координаты вектора
{2;1;-3}. Найдите координаты вектора 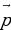 = 3
= 3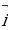 + 3
+ 3 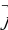 + 4
+ 4 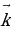 и
и 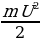 через 10 с после начала движения.
через 10 с после начала движения.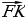 +
+ 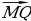 +
+ 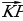 +
+ 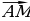 +
+ 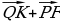
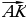 по векторам
по векторам 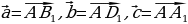
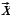 , начало и конец которого являются вершинами параллелепипеда, такой что
, начало и конец которого являются вершинами параллелепипеда, такой что 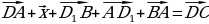 .
.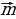 , заданного координатами
, заданного координатами 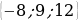
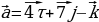 и
и 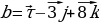 острый тупой или прямой?
острый тупой или прямой?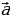
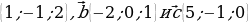
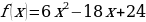 в точке
в точке 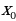 =5.
=5.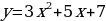 в точке.
в точке.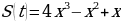 в момент времени
в момент времени 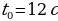 .
.