Координатная прямая.

Г. Хасавюрт, гимназия им. М.Горького, учитель математики Компанеец – Вовк В.Н.

Урок математики в 6 классе

«Положительные и отрицательные числа. Координатная прямая.»

Цели и задачи:

• познакомить учащихся с отрицательными числами;

• ввести понятие «координатной прямой», «целые числа», «рациональные числа», «противоположные числа», «координаты точки на прямой»;

• научить отмечать и определять точки на координатной прямой; пользоваться градусником;

• расширить знания учащихся об ученых математиках, о развитии теории чисел;

• использовать межпредметные связи (с историей, биологией, географией, экономикой) для повышения интереса к предмету;

• интегрировать координатную прямую и отрицательные числа в другие дисциплины для демонстрации практического применения математических знаний.

Форма урока:

урок изучения нового материала с использованием ИКТ

Оборудование урока:

Технические средства: ПК Pentium 4 (11 штук)

Интерактивная доска ActivBoard 378E100

Документ-камера ActiView 322

Программные продукты: Microsoft PowerPoint 2010 (5 презентаций),

Paint.net 2010 (рисунок координатной прямой),

ПО ActivInspire Professional Edition,

модули ЭОР к ОМС 1. М06_021_р01.oms

2. М06_021_k01.oms

Цифровые образовательные ресурсы:

Интерактивное учебное пособие: «Наглядная математика - 6 класс» из серии «Наглядная школа»

Интернет-ресурсы: http://www.prometheanplanet.ru/, http://interaktiveboard.ru/

http://festival.1september.ru, http://do.gendocs.ru/

http://nsportal.ru, http://prezentacii.com, http://www.uchportal.ru

Ход урока:

1. Организационный момент.

2. Введение:

Великий философ, математик, физик, живший в 17 веке, чье имя вы узнаете позже, говорил: «Уважение других дает повод уважения себя», «Я мыслю, следовательно, существую», «Мало иметь хороший ум, главное – хорошо его применять». Вот и мы с вами сегодня будем творить, уважая друг друга, осмысливая свои действия и применять на практике все свои умения.

Ребята мы закончили изучать Главу-1 «Обыкновенные дроби», написали контрольную работу, провели анализ, а теперь мы переходим к Главе–2 «Рациональные числа».

Вообще в жизни ученика 3 важных знакомства с числами!

- Знакомство с натуральными числами, в 1 классе. Для чего они служат?

(счет предметов)

- Знакомство с дробными числами, в 5 классе. Для чего они служат?

(счет долей, частей)

( На интерактивной доске воспроизводится Презентация 1)

- (слайд 1.1) И наконец, знакомство с отрицательными числами. Что это за числа и где применяются, для чего служат мы и узнаем сегодня на уроке.

А еще мы познакомимся с целыми и рациональными числами, научимся пользоваться градусником, определять и отмечать точки на координатной прямой.

Ребята, запишите число и тему урока.

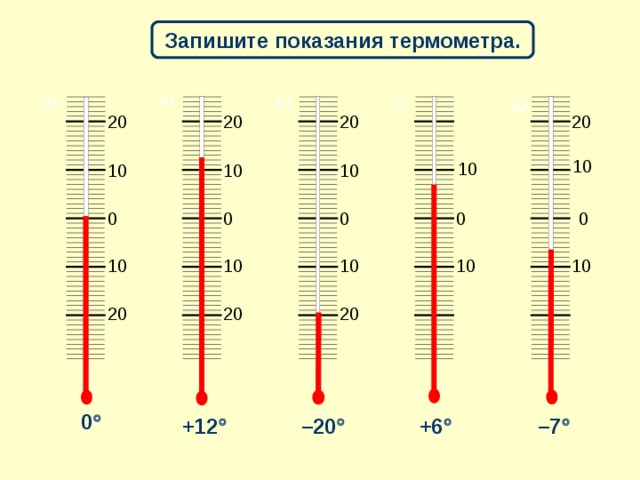
1. Шкала на термометре.

Шкала есть на каждом термометре. Термометр - это прибор для измерения температуры. Какую температуру показывают термометры?

(Слайд 1.2) 10 градусов тепла или 10 градусов выше нуля или плюс 10 градусов

(Слайд 1.3) 0 градусов

(Слайд 1.4) 9градусов мороза или 9 градусов ниже нуля или минус 9 градусов.

1. Ученик 1: Отрицательные числа и долг (слайд 1.5)

Отрицательное число с древних времен ассоциируется со словом «долг», тогда как положительное число можно ассоциировать со словами «наличие» или «доход». Значит, положительные целые и дробные числа при вычислениях — это то, что мы имеем, а отрицательные целые и дробные числа — это то, что составляет долг. Греки тоже поначалу знаков не использовали, пока в III веке Диофант Александрийский не стал обозначать вычитание знаком. В Италии ростовщики, давая деньги в долг, ставили перед именем должника сумму долга и черточку, вроде нашего минуса, а когда должник возвращал деньги, зачеркивали ее, получалось что-то вроде нашего плюса. Можно же плюс считать зачеркнутым минусом!

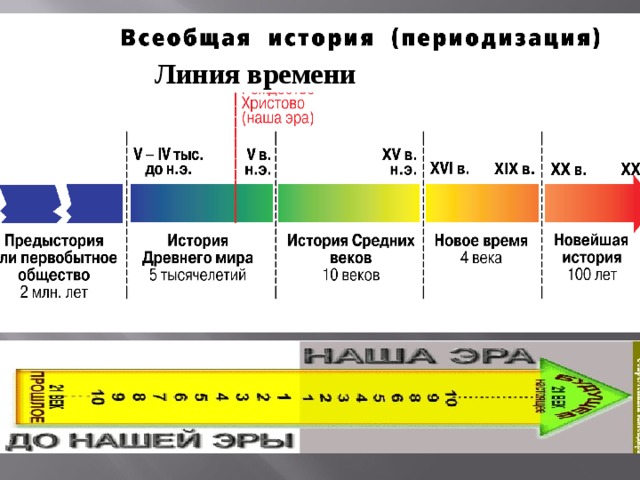
Ученик 2: Линия времени (слайд 1.6).

Знакомы вам такие фразы: «Пифагор жил в VI веке до нашей эры»; «Русь находилась под игом монголо-татар в течении XIII-XV веков нашей эры»?

В древности года в разных странах считали по разному. Например, в Древнем Египте каждый раз, когда начинал править новый царь, счет лет начинал править новый царь, счет лет начинался заново, римляне первым годом считали год основания своего города. Такой счет прошедших лет был неудобен для определения важных исторических событий. Возникла необходимость во всех странах начать вести счет времени от данного события. В это время христианская религия, вера в Иисуса Христа распространилась во многих странах. Один из верующих предложил вести счет лет от рождения Иисуса. Время, исчисляемое от Рождества Христова стали называть наша эра, которая ассоциируется с положительными числами. Продолжается наша эра две тысячи лет. Время, исчисляемое до Рождества Христова - до нашей эры, ассоциируется с отрицательными числами.

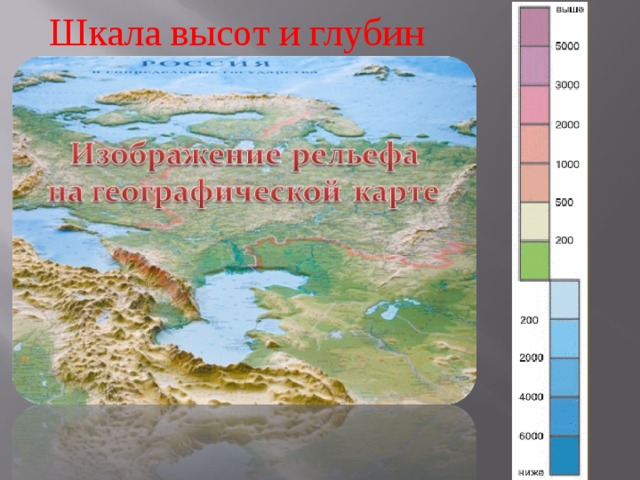
Ученик 3: Шкала высот и глубин. (слайд 1.7).

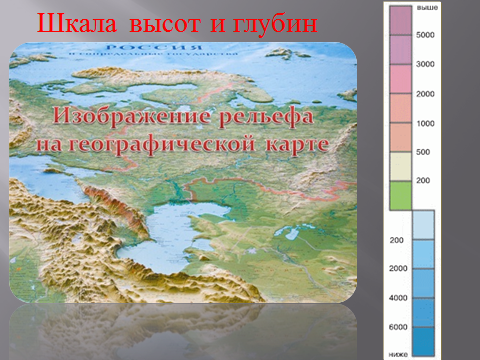
На уроках географии мы изучали шкалу высот и глубин. На ней начало отсчета ведется от уровня океана. Все что выше данного уровня ассоциируется с положительными числами, то что ниже - с отрицательными. Поверхность нашей Земли представлена равнинами и горами их высота определяется по шкале; по ней же определяется глубина океанов. Шкала цветовых тонов, используемых для гипсометрической окраски высотных ступеней. Обычно для низменностей (выс. от 0 до 200 м) используют тона зелёного цвета с уменьшением вверх их интенсивности, для ступеней выше 200 м – тона жёлтого, коричневого, красновато-коричневого цвета с увеличением вверх их насыщенности. Так выглядят шкалы, построенные по принципу «чем выше, тем темнее». Для ступеней морских глубин используют голубые и синие цвета. Шкалы высот и глубин применяют на гипсометрических, учебных общегеографических и физических картах. Саму шкалу с указанием высот дают на полях карты.

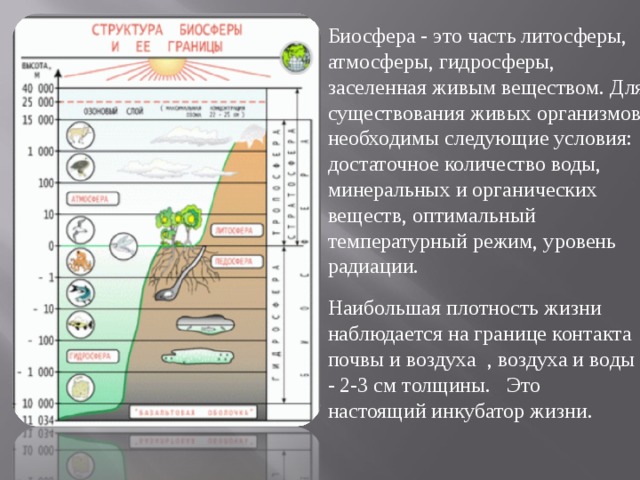
Ученик 4: Таблица «Биосфера» (слайд 1.8).

На таблице «Биосфера» показана шкала распределения плотности жизни от уровня поверхности Земли, Иначе говоря, биосфера - это часть литосферы, атмосферы, гидросферы, заселенная живым веществом. Для существования живых организмов необходимы следующие условия: достаточное количество воды, минеральных веществ, оптимальный температурный режим, уровень радиации и др. Плотность жизни в биосфере Распределение жизни в биосфере носит резко неравномерный характер. Наибольшая плотность жизни наблюдается на границах сред обитания, например почвы и воздуха - 2-3 см толщины, а так же воздуха и воды - это настоящий инкубатор жизни.

1. Ученик 5: «О развитии теории чисел»

Натуральные числа возникли при счёте предметов. Но результат измерений не всегда выражался в целых числах. Поэтому были введены дробные числа и число 0. Так в ходе практической потребности людей расширялось понятие числа. Но бывало и так, что задачи самой математики требовали расширения понятия чисел. Так введением дробных чисел стало возможным делить любое целое число на другое целое (=0). Так ученые могли решить любое уравнение вида: x 10 = 2. А вот уравнение вида x+ 10 = 2 они решить не могли. Для решения таких уравнений и были введены отрицательные числа. Положительные числа изображали палочками красного цвета, а отрицательные - палочками черного цвета. Первые сведения об отрицательных числах встречаются у китайских математиков во II в до н.э. Положительные числа тогда толковались как имущество, а отрицательные - как долг, недостача. Индийские математики лишь в VII в н.э. начали широко использовать отрицательные числа. В Европе отрицательными числами начали пользоваться в XII- XIII в.в. Окончательное и всеобщее признание отрицательные числа получили лишь в первой половине XVIII в. Тогда же утвердилось и совершенное обозначение для отрицательных чисел.

1. Объяснение новой темы:

1) Итак, вы познакомились с отрицательными числами. Увидели где и как они применяются.

(Слайд 1.9) Числа со знаком «+» называют положительными. Числа со знаком «-» называют отрицательными. Положительные числа (целые и дробные), отрицательные числа (целые и дробные) и число 0 составляют группу рациональных чисел. Рациональные числа обозначаются большой латинской буквой R.

(Уч-ся записывают в тетрадях материал со слайда 1.9)

1. Постройте координатный луч на правой стороне тетрадного листа, начиная с середины листа (ученик комментирует построение). За единичный отрезок возьмите 1 клетку. Отметьте на координатном луче число 1; число 4; число 6.

Постройте дополнительный луч, на нем от точки О влево отложите аналогичные единичные отрезки. Отметьте на дополнительном луче число -1; число -4; число -6, влево от 0.

На координатной прямой положительные числа расположены справа от начала отсчета точки О, отрицательные слева. Перед числами которые расположены слева от точки О ставят знак минус, справа от точки О ставят знак + (или просто его опускают, как это делали мы раньше).

У нас получилась? (координатная прямая) (Слайд 1.10)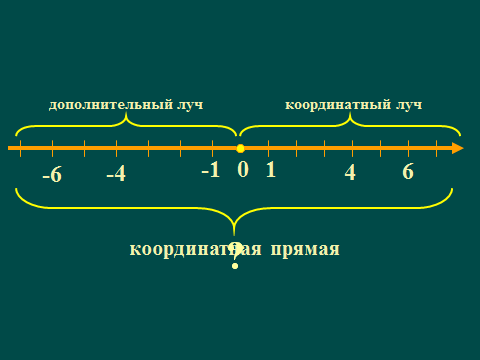

Уч-ся выполняют построения в тетрадях, учитель работает на интерактивной доске. Перед учащимися координатная прямая предстает в анимационном виде в определенной последовательности: (сначала знакомый числовой луч с точками, затем дополнительный луч для нанесения отрицательных чисел).

1. (Слайд 1.11)

Прямую с выбранными на ней началом отсчета, единичным отрезком и направлением называют координатной прямой. Она может располагаться и горизонтально (как на ленте времени) и вертикально (как на термометре).

1. (Слайд 1.12)

Противоположные числа – это числа, которые отличаются только знаком. Например: +3 и -3; -0,2 и + 0,2 и т.п.

Целые числа – это натуральные числа, противоположные им числа и число 0. (уч-ся записывают примеры противоположных чисел)

1. (Слайд 1.13)

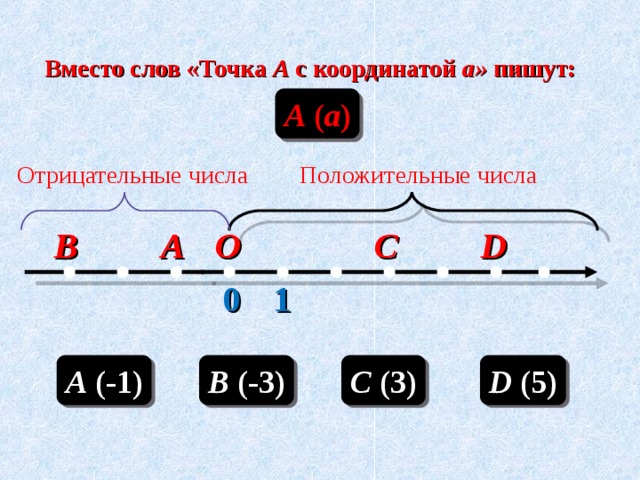
Число, показывающее положение точки на прямой, называют координатой этой точки. Вместо слов «точка А с координатой а» пишут А(а). В тетрадях выпишите координаты точек (проверка с помощью интерактивной доски)

Промежуточный итог:

(шуточный в стихах, читает ученица в образе координатной прямой)

Вы запомнили: Кто я такая? Я - Координатная прямая!

Я прямая без сомненья и имею направленье,

Для облегчения подсчёта, 0 – начало для отсчёта.

У меня есть много дочек – Красивых ярких точек.

Координатной точки является что? Положение что показывает число:

Справа от начала 0 положительное звено: Плюс 1, плюс 3, плюс 5,

Плюсов их не сосчитать; А слева отрицательные,

Не доброжелательные, Числа минус впереди. Лучше с ними не шути!

Посередине никакой расположился важный ноль

Без минусов, не идеален, и как все нули нейтрален.

Если ученье не прошло в пустую, решим задачи мы простые.

1. Закрепление

1. Как построить координатную прямую? (Презентация 2)

(провести прямую; отметить на ней начало отсчета; задать единичный отрезок;

указать направление) (Слайды 1-3)

На интерактивной доске в анимационном режиме уч-ся проходят мини-тест.

1. (Презентация 3)

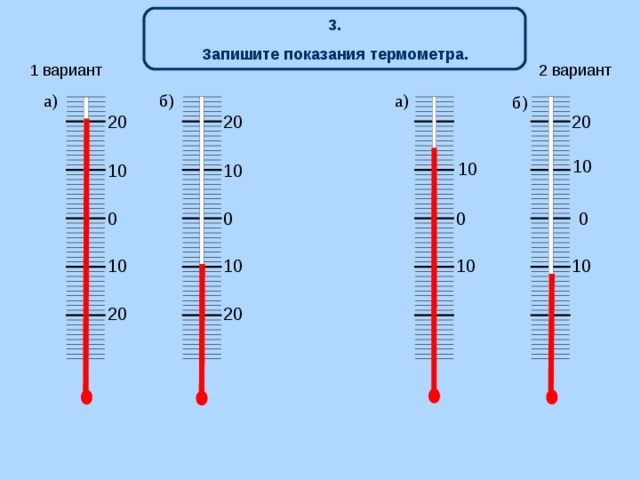
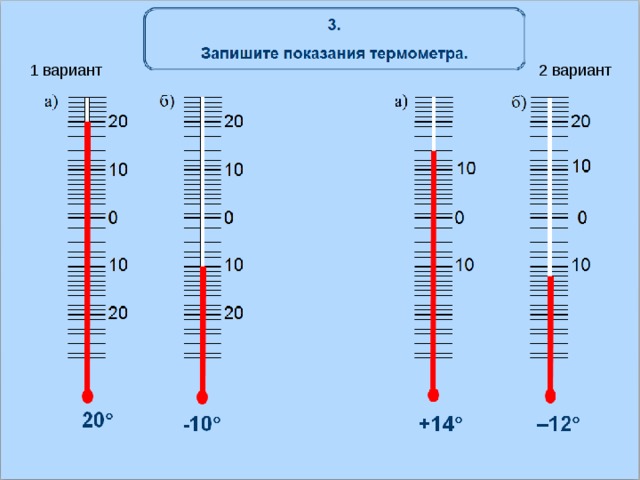
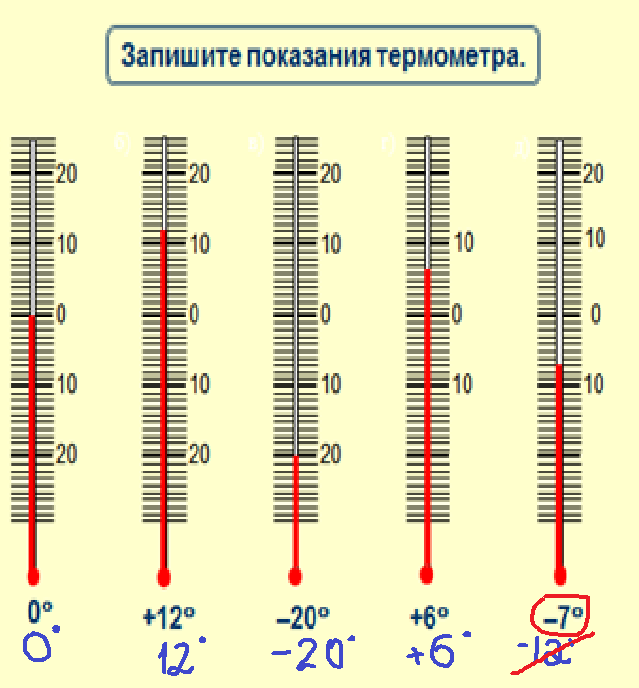
Задание№1: Записать показания термометров. (Слайд 3.1)

Уч-ся у на интерактивной доске делают записи поверх слайда, учитель проверяет с помощью всплывающего ответа.

1. Задание №2: (Слайд 3.2)

Сначала отметить числа, которые располагаются на луче (положительные), затем те которые можно отметить на прямой (т.е. и отрицательные)

Ученики работают в тетрадях, 1 уч-ся работает у интерактивной доски, нажимая пером на нужную точку.

1. (Презентация №4)

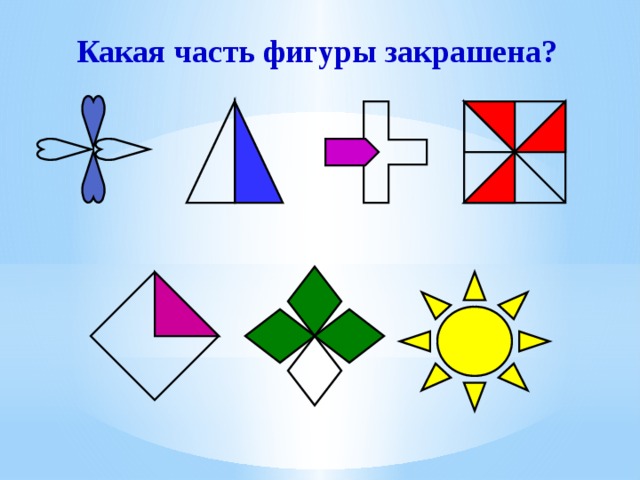
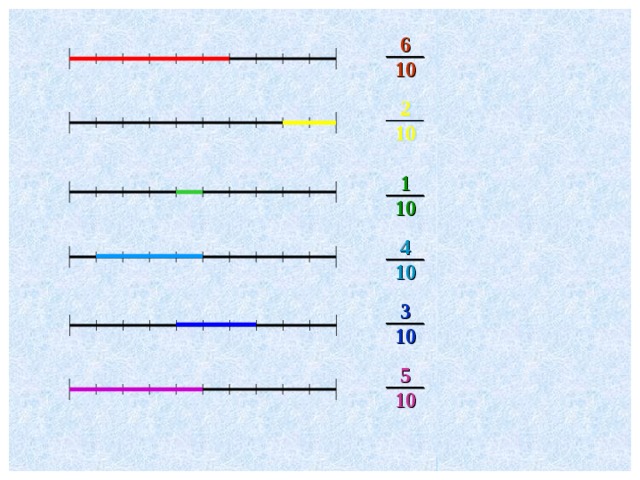
Упражнения на формирование умений определять координаты точки, выраженные обыкновенными дробями. (Слайд 4.1)

Ребята отвечают, какая часть фигуры и какая часть отрезка закрашена (слайд 4.2 – 4.3)

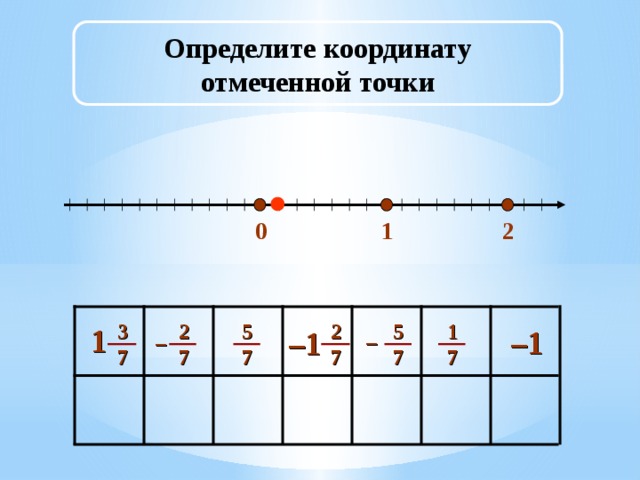
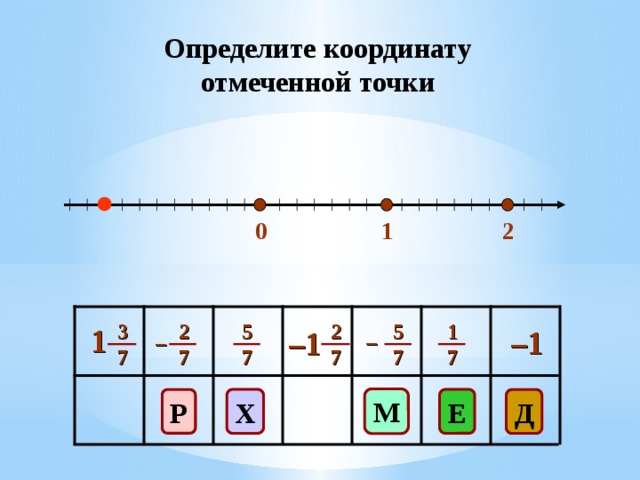
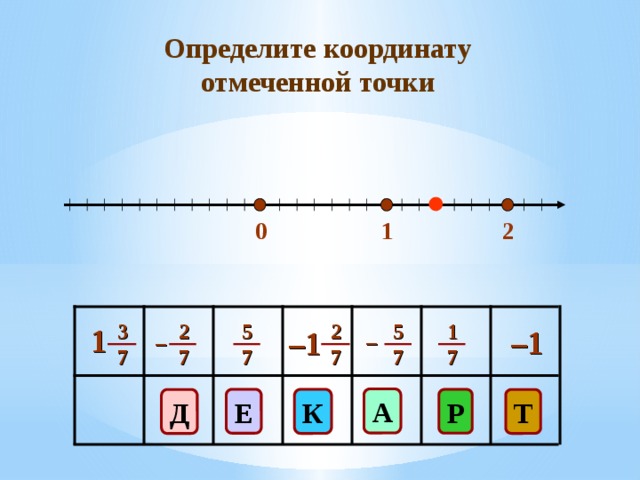
Далее уч- ся определяю координаты отмеченных точек (точки всплывают постепенно). Если определяют правильно, то всплывает буква. Если не правильно, то программа их предупреждают об ошибке - (Слайд 4.13).

(Слайды 4.4 – 4.10)

Получившееся слово - Рене Декарт: (слайд 4.12)

Ученица: Виктория Николаевна начала наш урок цитатами: «Уважение других дает повод уважения себя», «Я мыслю, следовательно, существую», «Мало иметь хороший ум, главное – хорошо его применять». Эти слова принадлежат Рене Декарту, французскому математику, физику и философу, жившему в период с 1596 по 1650г. В 1637 году он предложил геометрическое истолкование положительных и отрицательных чисел, ввел координатную прямую. (слайд 4.12)

1. Задание №3: Указать местоположение данных чисел на координатной прямой ось х: х = 1, х =3, х = -1

Ось у: х = -2.5, х = 1/3, х = 4,5 (Слайд 3.3)

С осью Х работает более слабый учащийся (целые числа), с осью У более сильный (дробные числа). (Числа всплывают по мере решения на интерактивной доске).

1. Работа с интерактивным учебным пособием «Наглядная математика – 6 класс» (работа в парах на готовой координатной прямой). Остальные учащиеся работают в тетрадях. По окончании работы учитель проверяет некоторых учащихся используя док.камеру.

Задание №4:

Вариант 1: один уч-ся называет точки с целочисленными координатами, другой их отмечает на координатной прямой. Например А(4), В(7), С(-5)

(в данной паре оценивается тот, кто отмечает числа);

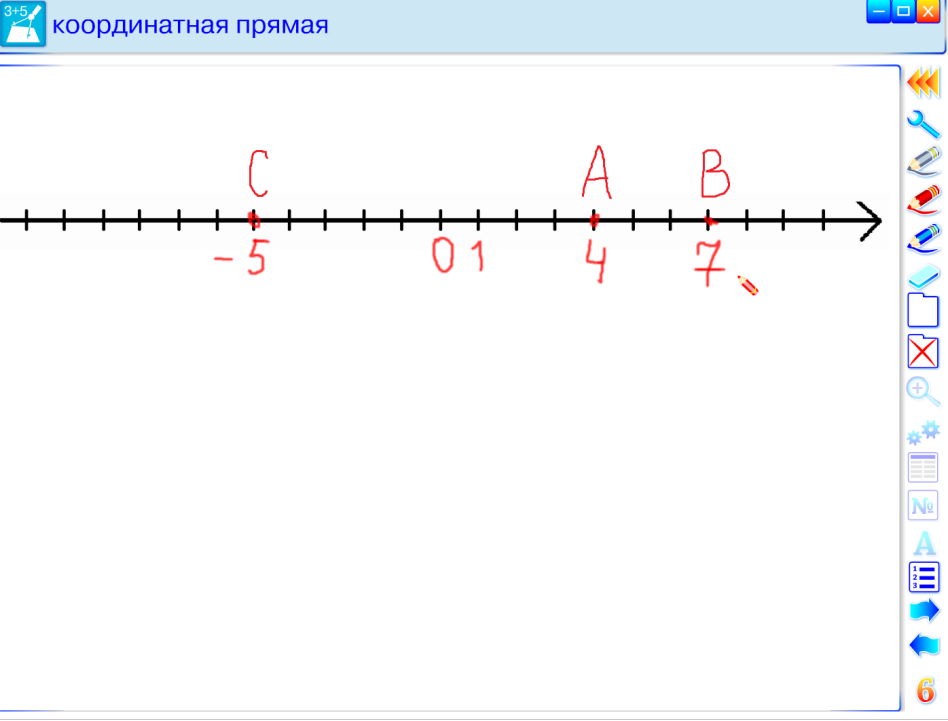
Вариант2: так же только с дробными числами. Ребятам самим нужно выбрать единичный отрезок. Например: единичный отрезок равен 6 делениям. Точки М (2/6) и т.п. (в данной паре оцениваются оба).

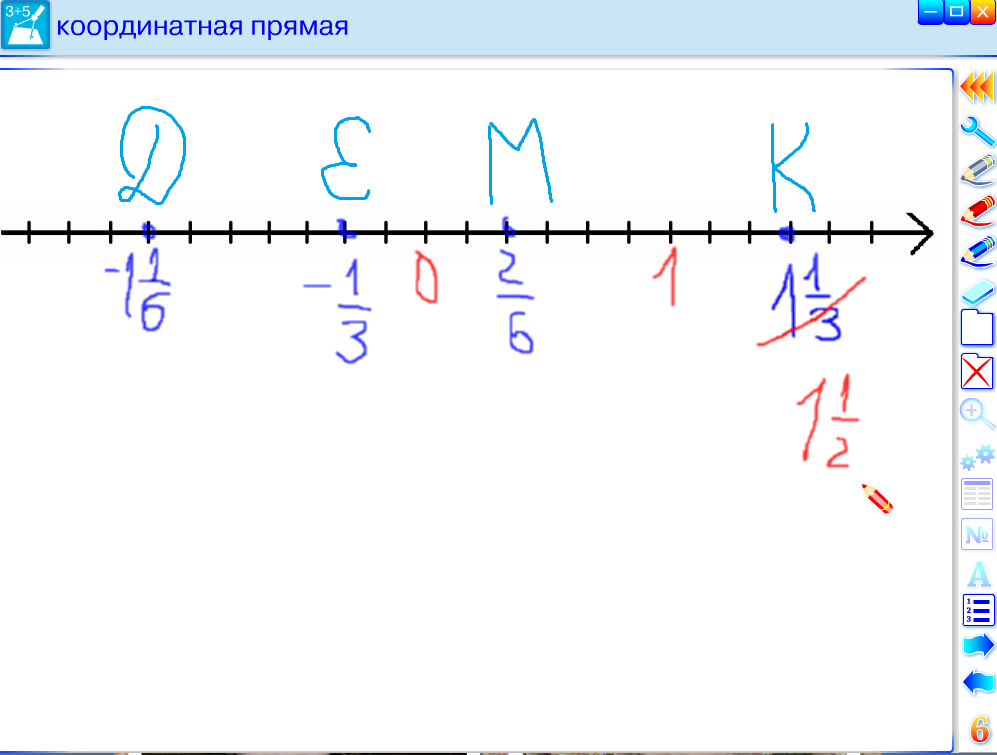
1. Этап контроля:

1. После проверки правильности выполнения работы в тетрадях, учащиеся с медленной скоростью работы (11 человек) садятся за компьютеры, на которых установлены ОМС плееры с загруженными модулями.

М06_021_р01.oms (для более слабых уч-ся)

И М06_021_k01.oms (для более сильных уч-ся)

и выполняют проверочную работу. Учащиеся выполняют только Задание 1 модулей.

Правильность выполнения задания выполняется при просмотре окна Статистика.

1. (Презентация №5)

Остальная часть класса работает с интерактивной доской, выполняет математический диктант с последующей самопроверкой.

1. Итоги:

Работа с интерактивным учебным пособием «Наглядная математика – 6 класс»

Вопросы:

1. Что вы узнали нового на уроке?

2. Какие числа называются положительными? отрицательными?

3. Какое число не положительно и не отрицательное?

4. Что такое координатная прямая?

5. Что называется координатой точки на прямой?

6. Какую координату имеет начало координат?

7. Что такое противоположные числа?

8. Что такое целые числа?

Рефлексия:

1. Считаете ли вы, что усвоили тему урока?

2. Понравился вам урок?

1. Оценки.

2. Домашнее задание: п.26, №904, №905

(учебник Н.Я. Виленкин «Математика 6 класс»)

8

Г. Хасавюрт, гимназия им. М.Горького, учитель математики Компанеец – Вовк В.Н.

1

Цели:

• Познакомиться:

- с отрицательными числами; целыми числами;

противоположными числами;

• с координатной прямой;

2) Научиться:

• отмечать точки на координатной прямой с заданными координатами;
• определять координаты точек на прямой.

20

1 0 градусов тепла

10

0

10 градусов выше нуля

10

+10º,С (плюс 1º,С)

20

20

10

0

0º,С

10

20

20

9 градусов мороза

10

0

9 градусов ниже нуля

10

-9 о ,С (минус 9 о ,С)

20

Отрицательное число с древних времен ассоциируется со словом «долг», тогда как положительное число можно ассоциировать со словами «наличие» или «доход».

Линия времени

Шкала высот и глубин

Биосфера - это часть литосферы, атмосферы, гидросферы, заселенная живым веществом. Для существования живых организмов необходимы следующие условия: достаточное количество воды, минеральных и органических веществ, оптимальный температурный режим, уровень радиации.

Наибольшая плотность жизни наблюдается на границе контакта почвы и воздуха , воздуха и воды - 2-3 см толщины. Это настоящий инкубатор жизни.

+1

7

+7

положительные числа

20

не является

ни положительным,

ни отрицательным числом

0

-20

-7

-1

отрицательные числа

-14

дополнительный луч

координатный луч

-1

1

0

6

4

-4

-6

?

координатная прямая

F

С

Координатная прямая – это прямая с указанными на ней:

Р

• началом отсчета,
• направлением отсчета,
• единичным отрезком

D

В

А

1

А

O

0

K

Е

Х

А

O

K

N

0

1

Вместо слов «Точка А с координатой а» пишут:

А ( а )

Положительные числа

Отрицательные числа

B

O

D

C

A

1

0

A (-1)

B (-3)

C (3)

D (5)

Какие из этих прямых являются координатными

2

1

3

В

D

А

0

1

O

0

F

M

O

5

4

C

6

0

5

2

3,4,5

2,3,4,5

1,2,3,4,5

3

ОШИБКА

Запишите показания термометра.

в)

г)

б)

а)

д)

20

20

20

20

10

10

10

10

10

0

0

0

0

0

10

10

10

10

10

20

20

20

0 

+6 

– 20 

+12 

– 7 

Х

О

6

8

3

1

-2

-5

0

-7

А на координатной прямой?

x = 1

x = 3

ось x

x = -1

-1

3

1

1

0

y = -2,5

y = 1 / 3

ось y

y = 4 ,5

4 ,5

1

-2,5

0

1 / 3

Математический диктант

1 вариант

2 вариант

1.

Запишите координаты отмеченных точек:

A B O M C

A B O М C

0 1

0 1

2 .

Запишите координату точки противоположной данной, относительно точки O (0) :

а) – 6,43

а) 3

б) 4.7

б) – 4

3.

Запишите показания термометра.

1 вариант

2 вариант

б)

а)

а)

б)

20

20

20

10

10

10

10

0

0

0

0

10

10

10

10

20

20

1 вариант

2 вариант

Упражнения

на формирование умений определять координаты точки, выраженные обыкновенными дробями.

Какая часть фигуры закрашена?

6

10

2

10

1

10

4

10

3

10

5

10

Определите координату отмеченной точки

0

2

1

1

5

2

5

2

3

7

7

7

7

7

7

1

– 1

– 1

–

–

Определите координату отмеченной точки

2

1

0

5

1

2

3

2

5

7

7

7

7

7

7

1

– 1

– 1

–

–

Р

Определите координату отмеченной точки

1

2

0

5

2

3

2

1

5

7

7

7

7

7

7

1

– 1

– 1

–

–

Р

Т

Определите координату отмеченной точки и узнайте имя знаменитого математика.

2

1

0

2

5

3

2

5

1

7

7

7

7

7

7

1

– 1

– 1

–

–

Р

Д

Т

Определите координату отмеченной точки

2

1

0

5

3

1

2

5

2

7

7

7

7

7

7

1

– 1

– 1

–

–

Е

Р

Т

Д

Определите координату отмеченной точки

2

1

0

3

2

5

1

5

2

7

7

7

7

7

7

1

– 1

– 1

–

–

М

Х

E

Р

Д

Определите координату отмеченной точки

0

2

1

5

2

2

5

1

3

7

7

7

7

7

7

1

– 1

– 1

–

–

А

К

Е

Р

Т

Д

Определите координату отмеченной точки

1

0

2

2

5

2

5

3

1

7

7

7

7

7

7

1

– 1

– 1

–

–

А

Р.

К

Е

Р

Т

Д

РЕНЕ ДЕКАРТ

(1596-1650)

«Я мыслю, следовательно, я существую».

Французский математик, физик и философ. В 1637 году предложил геометрическое истолкование положительных и отрицательных чисел - ввел координатную прямую.

• О

ш

и

б

к

а

!!!