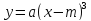Кубической называется функция, заданная формулой 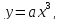 где а ≠ 0
где а ≠ 0
I. Частным случаем кубической функции является функция 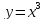 , здесь a = 1, b = c = d = 0.
, здесь a = 1, b = c = d = 0.
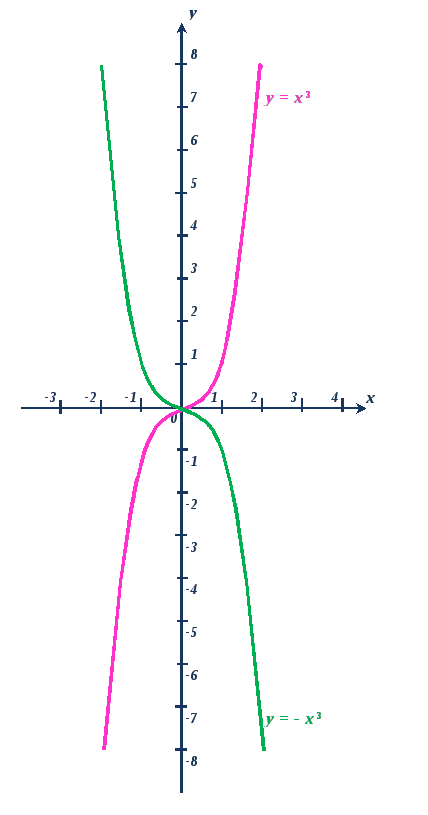
Графиком кубической функции y = x3 является кубическая парабола с вершиной в точке (0;0), проходящая через точки (1;1), (-1;-1), (2;8), (-2;-8) (запомнить эти точки), располагается в I и III четвертях.
1) Область определения функции - множество всех действительных чисел: D(y)=(− ; +
; + ).
).
2) Область значений функции – множество всех действительных чисел: Е(y) = (− ; +
; + ).
).
3) y(-x) = (-x)3 = - x3 = - y(x). Значит, кубическая функция является нечётной, её график симметричен относительно начала координат, т.е. точки (0;0).
4) Функция возрастает при х 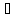 (−
(− ; +
; +  ).
).
II. Кубическая функция 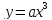 , здесь a ≠ 0
, здесь a ≠ 0
Графиком кубической функции y = ax3 является кубическая парабола с вершиной в точке (0;0), проходящая через точки (1;1a), (-1;-1a), (2;8a), (-2;-8a)), располагается в I и III четвертях, если a0, и во II и IV четвертях, если a.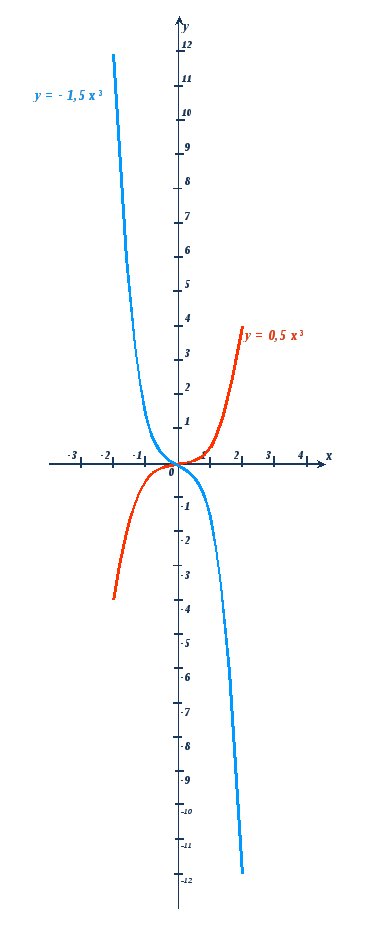
1) Область определения функции - множество всех действительных чисел: D(y)=(− ; +
; + ).
).
2) Область значений функции – множество всех действительных чисел: Е(y) = (− ; +
; + ).
).
3) y(-x) = a(-x)3 = - ax3 = - y(x). Значит, кубическая функция является нечётной, её график симметричен относительно начала координат, т.е. точки (0;0).
4) При a0 функция возрастает при х 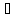 (−
(− ; +
; +  ).
).
При a, функция убывает при х  (−
(− ; +
; +  ).
).
III. Кубическая функция 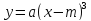
Графиком кубической функции 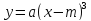 является кубическая парабола с вершиной в точке (m;0). График функции
является кубическая парабола с вершиной в точке (m;0). График функции 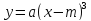 получается из графика функции
получается из графика функции  смещением вдоль оси Ox на m единиц .
смещением вдоль оси Ox на m единиц .
1) Область определения функции - множество всех действительных чисел: D(y)=(− ; +
; + )
)
.
2) Область значений функции – множество всех действительных чисел: Е(y) = (− ; +
; + ).
).
3) y(-x) = a(-x - m)3 = - a(x + m)3 ≠ y(x) ≠ - y(x). Значит, данная кубическая функция не является ни чётной, ни нечётной.
4) При a0 функция возрастает при х 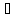 (−
(− ; +
; +  ).
).
При a, функция убывает при х 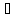 (−
(− ; +
; +  ).
).
IV. Кубическая функция 
Графиком кубической функции  является кубическая парабола с вершиной в точке (0; n). График функции
является кубическая парабола с вершиной в точке (0; n). График функции  получается из графика функции
получается из графика функции  смещением вдоль оси Oy на n единиц .
смещением вдоль оси Oy на n единиц .
1) Область определения функции - множество всех действительных чисел: D(y)=(− ; +
; + )
)
.
2) Область значений функции – множество всех действительных чисел: Е(y) = (− ; +
; + ).
).
3) y(-x) = a(-x)3 + n = - ax3 + n ≠ y(x) ≠ - y(x). Значит, данная кубическая функция не является ни чётной, ни нечётной.
4) При a0 функция возрастает при х 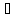 (−
(− ; +
; +  ).
).
При a, функция убывает при х 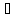 (−
(− ; +
; +  ).
).
V. Кубическая функция 
Графиком кубической функции  является кубическая парабола с вершиной в точке (m; n). График функции
является кубическая парабола с вершиной в точке (m; n). График функции  получается из графика функции
получается из графика функции  смещением вдоль оси Оx на m единиц, а вдоль оси Oy на n единиц .
смещением вдоль оси Оx на m единиц, а вдоль оси Oy на n единиц .
1) Область определения функции - множество всех действительных чисел: D(y)=(− ; +
; + )
)
.
2) Область значений функции – множество всех действительных чисел: Е(y) = (− ; +
; + ).
).
3) y(-x) = a(-x)3 + n = - ax3 + n ≠ y(x) ≠ - y(x). Значит, данная кубическая функция не является ни чётной, ни нечётной.
4) При a0 функция возрастает при х  (−
(− ; +
; +  ).
).
При a, функция убывает при х  (−
(− ; +
; +  ).
).







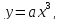 где а ≠ 0
где а ≠ 0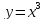 , здесь a = 1, b = c = d = 0.
, здесь a = 1, b = c = d = 0.  ; +
; +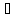 (−
(−
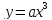 , здесь a ≠ 0
, здесь a ≠ 0