Конспект урока
Учебник: Алгебра, 8 класс : учеб. для общеобразоват. учреждений / [Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.] – 17-е изд. – М. : Просвещение, 2010. Глава V, §37 - 39
Тема урока: Квадратичная функция, её свойства и график
Тип урока: Урок-семинар
Учебная задача урока: в ходе докладов учащихся изучить построение графиков функций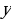 =
=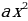 и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐.
и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐.
Учебные действия, формируемые на уроке:
Личностные: устанавливать связь между целью учебной деятельности и ее мотивом;
определять общие для всех правила поведения ;
определять правила работы в группах;
оценивать усваиваемое содержание (исходя личностных ценностей);
устанавливать связь между целью деятельности и ее результатом.
Регулятивные: определять и формулировать цель деятельности на уроке; проговаривать последовательность действий на уроке; работать по
плану, инструкции;
высказывать свое предположение на основе учебного материала;
отличать верно, выполненное задание от неверного;
осуществлять самоконтроль;
совместно с учителем и одноклассниками давать оценку деятельности
на уроке.
Коммуникативные: формулирование и аргументация своего мнения в коммуникации; владеть диалогической формой речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Познавательные: находить ответы на вопросы в тексте, иллюстрациях, используя свой жизненный опыт; проводить анализ учебного материала; проводить классификацию учебного материала, указывая на основание
классификации.
Методы обучения: УДЕ, частично-поисковые, репродуктивный
Форма работы: групповая, фронтальная
Средства обучения: традиционные, презентация
Структура урока:
Мотивационно-ориентировочная часть (2 минуты)
Содержательная часть (41 минута)
Рефлексивно-оценочная часть (2 минуты)
Подготовка к семинару
За 2 недели до семинара учитель разбивает учащихся на группы и дает задание каждой группе.
1 группа:
График функции 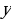 =
=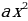 при
при 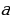 1 и её свойства
1 и её свойства
Литература:
Кириллова С.В., Огурцова О.К. Элементарная математика: Элементарные функции: Методические рекомендации для студентов математического факультета. – Н.Новгород.: НГПУ, 2006.- 43 с.
Ажулаева П.М. Методическое пособие по учебной дисциплине математика. Раздел: «Функции, их свойства и графики».– Нягань.: НТК, 2015.- 65 с.
Ткачева М.В., Шабунин М.И., Федорова Н.Е.: Алгебра. Дидактические материалы. 8класс. - 2-е изд., дораб. – М.: Просвещение, 2013. – 96с.
2 группа:
График функции 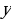 =
=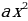 при
при 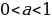 и её свойства
и её свойства
Литература:
Кириллова С.В., Огурцова О.К. Элементарная математика: Элементарные функции: Методические рекомендации для студентов математического факультета. – Н.Новгород.: НГПУ, 2006.- 43 с.
Ажулаева П.М. Методическое пособие по учебной дисциплине математика. Раздел: «Функции, их свойства и графики».– Нягань.: НТК, 2015.- 65 с.
Ткачева М.В., Шабунин М.И., Федорова Н.Е.: Алгебра. Дидактические материалы. 8класс. - 2-е изд., дораб. – М.: Просвещение, 2013. – 96с.
3 группа:
График функции 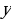 =
=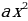 при a и её свойства
при a и её свойства
Литература:
Кириллова С.В., Огурцова О.К. Элементарная математика: Элементарные функции: Методические рекомендации для студентов математического факультета. – Н.Новгород.: НГПУ, 2006.- 43 с.
Ажулаева П.М. Методическое пособие по учебной дисциплине математика. Раздел: «Функции, их свойства и графики».– Нягань.: НТК, 2015.- 65 с.
Ткачева М.В., Шабунин М.И., Федорова Н.Е.: Алгебра. Дидактические материалы. 8класс. - 2-е изд., дораб. – М.: Просвещение, 2013. – 96с.
4 группа:
Построение графика функции 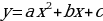 методом выделения полного квадрата
методом выделения полного квадрата
Литература:
Кириллова С.В., Огурцова О.К. Элементарная математика: Элементарные функции: Методические рекомендации для студентов математического факультета. – Н.Новгород.: НГПУ, 2006.- 43 с.
Ажулаева П.М. Методическое пособие по учебной дисциплине математика. Раздел: «Функции, их свойства и графики».– Нягань.: НТК, 2015.- 65 с.
Ткачева М.В., Шабунин М.И., Федорова Н.Е.: Алгебра. Дидактические материалы. 8класс. - 2-е изд., дораб. – М.: Просвещение, 2013. – 96с.
5 группа:
Построение графика функции y =ax2+bx+c с помощью алгоритма
Литература:
Ажулаева П.М. Методическое пособие по учебной дисциплине математика. Раздел: «Функции, их свойства и графики».– Нягань.: НТК, 2015.- 65 с.
Тюменцева О.Н. Методичесое пособие для самостоятельной работы студентов по дисциплине математика. Тема: «Функции».– Купино.: КМТ, 2020.- 36 с.
Бодряков В.Ю., Быков А.А., Ударцева Д.А. Квадратичная функция как мотивирующий инструмент решения экстремальных задач.– Ект.: ГСНТИ, 2007.- 63 с.
Ткачева М.В., Шабунин М.И., Федорова Н.Е.: Алгебра. Дидактические материалы. 8класс. - 2-е изд., дораб. – М.: Просвещение, 2013. – 96с.
За неделю до семинара учитель проверяет доклады учащихся и вывешивает план семинара.
План семинара
График функции 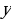 =
=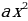 при
при 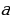 1 и её свойства
1 и её свойства
График функции 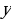 =
=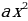 при
при 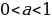 и её свойства
и её свойства
График функции 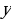 =
=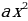 при a и её свойства
при a и её свойства
Построение графика функции 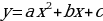 методом выделения полного квадрата
методом выделения полного квадрата
Построение графика функции y =ax2+bx+c с помощью алгоритма
Ход урока
Мотивационно-ориентировочная часть
-Вы все готовились к сегодняшнему уроку по разным темам. Поэтому сегодня на уроке вы заслушаете доклады каждой группы и изучите построение графиков функций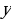 =
=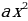 и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐.
и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐.
Содержательная часть
1 группа
Доклад на тему «График функции 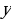 =
=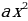 при
при 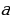 1 и её свойства»
1 и её свойства»
Пример 1.
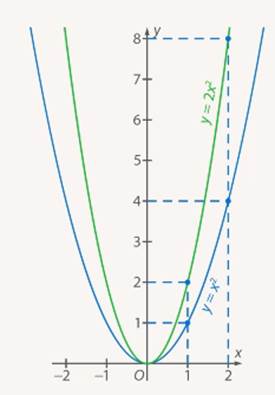
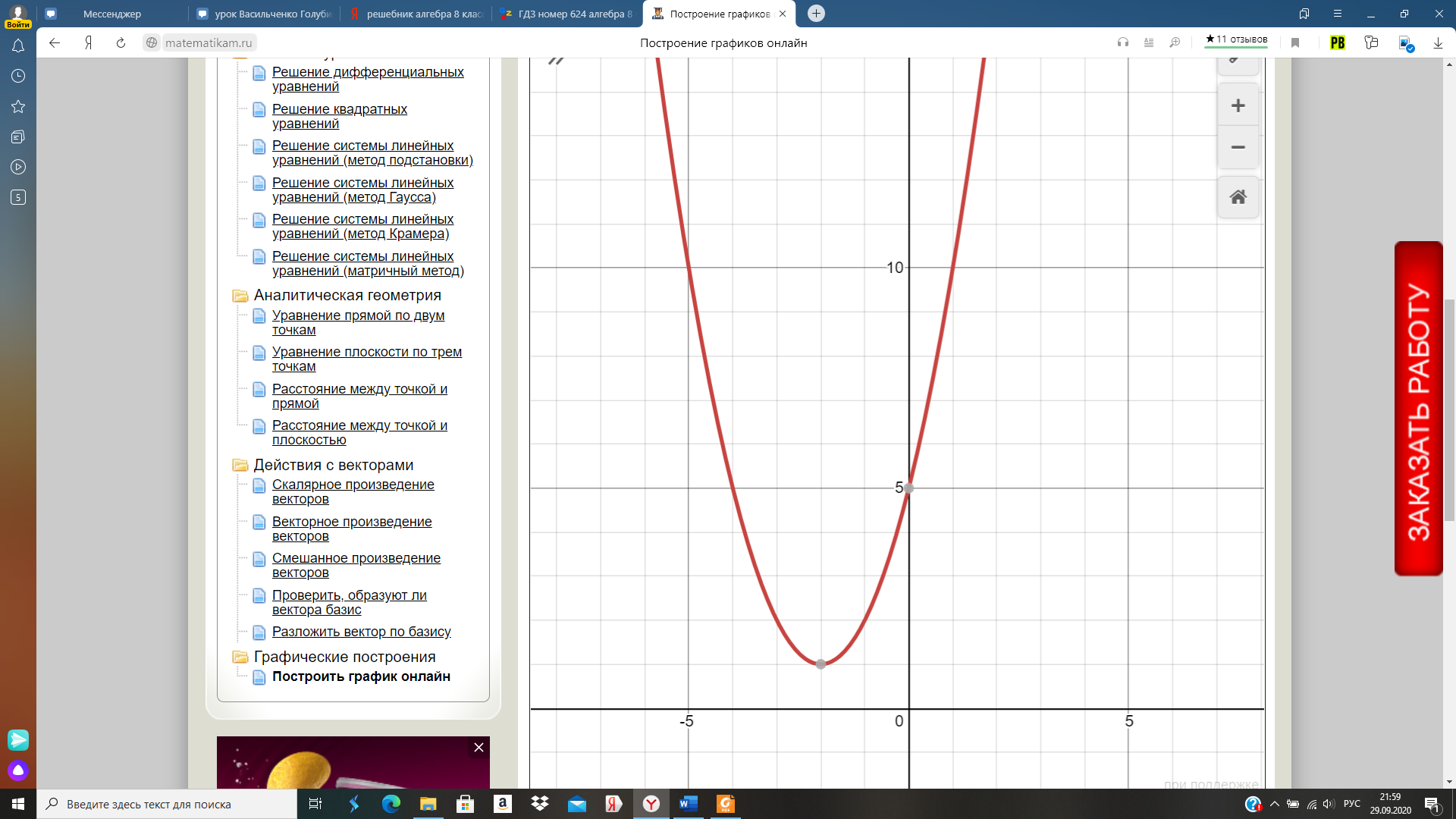
Построим график функции y = 2x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 2x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2x2 | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = 2x2 больше значений функции y = x2 в 2 раза. Графически это означает, что график функции y = 2x2 получается растяжением графика функции y = x2 от оси Ох вдоль оси Оу в 2 раза.
Пример 2.
Построим график функции y = 2,5x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 2,5x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2,5x2 | 22,5 | 10 | 2,5 | 0 | 2,5 | 10 | 22,5 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = 2,5x2 больше значений функции y = x2 в 2,5 раза. Графически это означает, что график функции y = 2,5x2 получается растяжением графика функции y = x2 от оси Ох вдоль оси Оу в 2,5 раза.
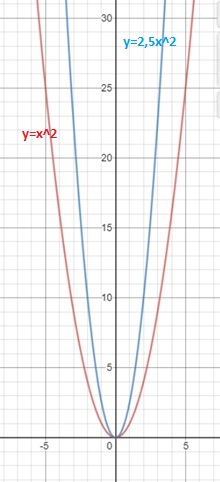
Таким образом, график функции y = ax2 при любом a1 можно также назвать параболой.
При a1 значения функции y = ax2 больше значений функции y = x2 в а раз, следовательно, график функции y = ax2 получается из графика функции y = x2 растяжением его в а раз от оси Ох вдоль оси Оу.
Свойства функции y = ax2 при a 1:
1. Если x = 0, то y = 0.
График функции проходит через начало координат – вершина параболы.
2. Если x ≠ 0, то y 0.
График функции расположен в верхней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает.
5. Функция принимает наименьшее значение, равно нулю, при x = 0.
6. Наибольшего значения функция не имеет, т.е. областью значений функции является промежуток [0; +∞).
7. Ветви параболы направлены вверх.
8. Фокус параболы находится в точке 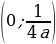 .
.
Квадратичная функция y = ax2 играет большую роль в познании реального мира. Рассмотрим несколько примеров парабол.
В физике можно рассмотреть следующие зависимости:
- мощности электрического тока P=I2R при постоянном сопротивлении,
- кинетической энергии E=mv2/2 при постоянной массе.
В природе встречается данный вид квадратичной функции, например, горы задают именно такую функцию.

Другой пример:

№ 595
2 группа
Доклад на тему «График функции 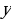 =
=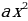 при
при 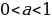 и её свойства»
и её свойства»
Пример 1.
Построим график функции y =  x2 и сравним его с графиком функции y = x2.
x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y =  x2
x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y =  x2 x2 | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y =  x2 меньше значений функции y = x2 в 2 раза. Графически это означает, что график функции y =
x2 меньше значений функции y = x2 в 2 раза. Графически это означает, что график функции y =  x2 получается сжатием графика функции y=
x2 получается сжатием графика функции y= вдоль оси Oy к оси Ox в 2 раза.
вдоль оси Oy к оси Ox в 2 раза.
Пример 2.
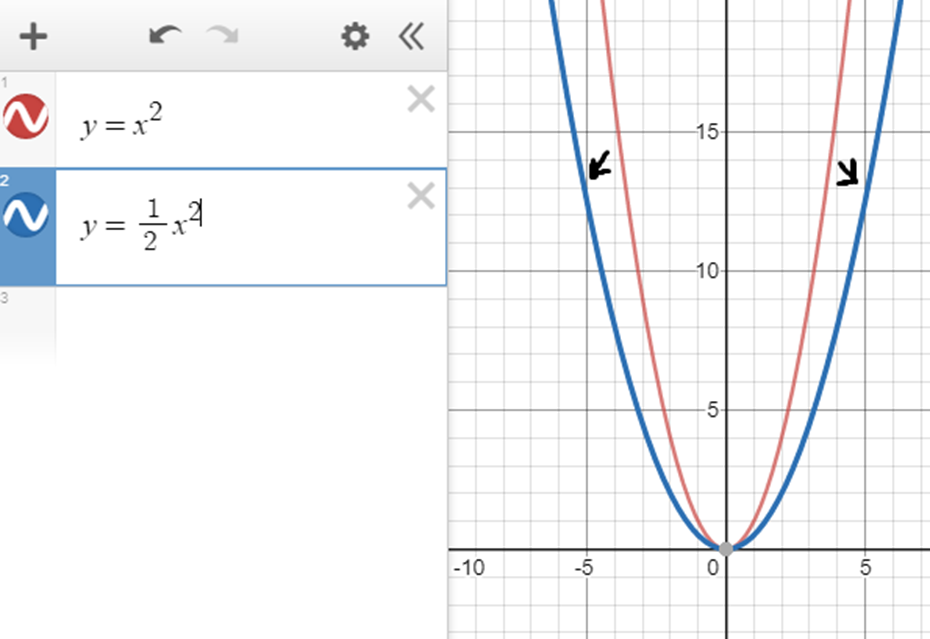
Построим график функции y = 0,2x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 0,2x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 0,2x2 | 1,8 | 0,8 | 0,2 | 0 | 0,2 | 0,8 | 1,8 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y =0,2x2 меньше значений функции y = x2 в 5 раз. Графически это означает, что график функции y = 0,2 x2 получается сжатием графика функции y= вдоль оси Oy к оси Ox в 5 раз.
вдоль оси Oy к оси Ox в 5 раз.
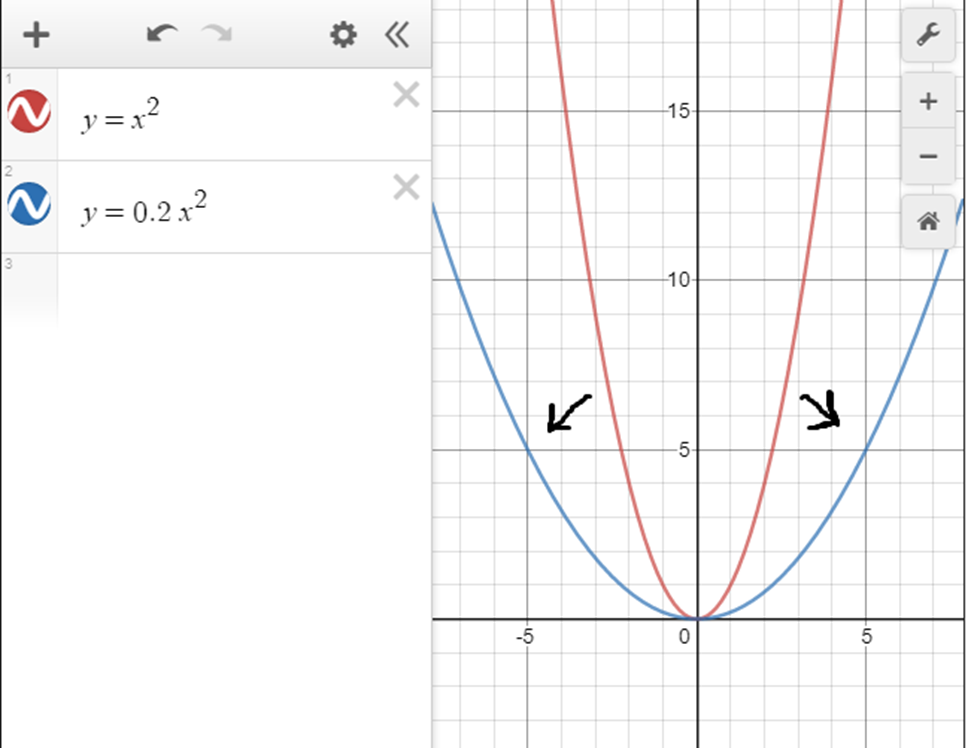
Таким образом, график функции y = ax2 при любом 0a можно также назвать параболой.
При 0a значения функции y = ax2 меньше значений функции y = x2 в 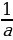 раз, следовательно, график функции y = ax2 получается из графика функции y = x2 сжатием его в
раз, следовательно, график функции y = ax2 получается из графика функции y = x2 сжатием его в 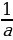 раз к оси Ох вдоль оси Оу.
раз к оси Ох вдоль оси Оу.
Свойства функции y = ax2 при 0a
1. Если x = 0, то y = 0.
График функции проходит через начало координат – вершина параболы.
2. Если x ≠ 0, то y 0.
График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает.
5. Функция принимает наименьшее значение, равно нулю, при x = 0.
6. Наибольшего значения функция не имеет, т.е. областью значений функции является промежуток [0; +∞).
7. Ветви параболы направлены вверх.
8. Фокус параболы находится в точке 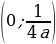 .
.
График квадратичной функции – парабола - довольно часто встречается в окружающей действительности. Например, это можно наблюдать в рампах, которые строятся для велосипедистов и скейтбордистов, а также в спутниковых тарелках.



Другой пример:
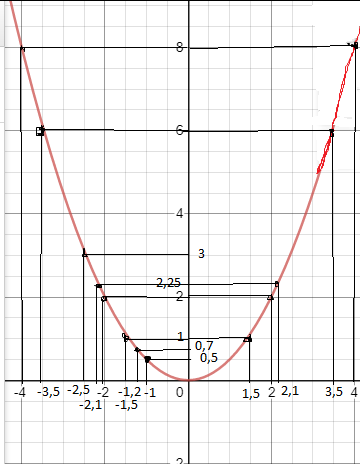
Задание: Постройте на милиметровой бумаге график функции y=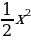 . По графику приближенно найти:
. По графику приближенно найти:
1) значения y, при x= -1; -1,2; -4; 2; -2,5.
2) значения x, если y= 1; 8; 2; 6; 2,25.
Решение:
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y =  x2 x2 | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 |
y(-1)=0,5
y(-1,2)≈0,7
y(-4)=8
y(2)=2
y(-2,5)=3
при y=1 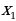 =-1,5,
=-1,5, 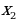 =1,5
=1,5
при y=8 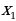 =-4,
=-4, 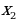 =4
=4
при y=2 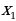 =-2,
=-2, 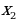 =2
=2
при y=6 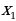 =-3,5,
=-3,5, 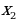 =3,5
=3,5
при y=2,25 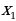 ≈-2,1,
≈-2,1, 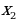 ≈2,1
≈2,1
3 группа
Доклад на тему «График функции 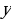 =
=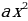 при a и её свойства»
при a и её свойства»
Пример 1. Построим график функции 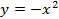 и сравним его с графиком функции y = x2.
и сравним его с графиком функции y = x2.
Составим таблицу значений функции y= .
.
| х | -1 | 0 | 1 | 2 |
| y = x2 | 1 | 0 | 1 | 4 |
Также составим таблицу значений функции y=−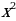
| х | -1 | 0 | 1 | 2 |
| y = x2 | -1 | 0 | -1 | -4 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = - x2 противоположны значениям функции y = x2. Графически это означает, что график функции y = - x2 получается отражением из графика функции y= от оси Ox
от оси Ox
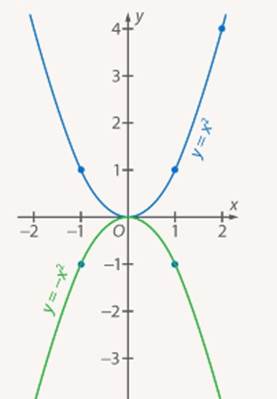
Пример 2. Построить график функции 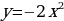 и сравним его с графиком функции y = 2x2.
и сравним его с графиком функции y = 2x2.
Составим таблицу значений функции y=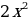 .
.
Также составим таблицу значений функции y=−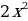
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = - 2 x2 противоположны значениям функции y = 2 x2 . Графически это означает, что график функции y = - 2 x2 получается отражением из графика функции y=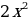 от оси Ox
от оси Ox
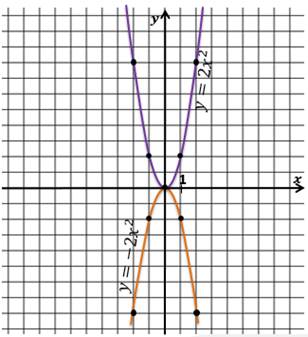
Таким образом, график функции y = ax2 при любом a можно также назвать параболой.
Чтобы построить график функции 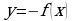 , надо построить график функции
, надо построить график функции 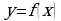 , а затем все точки этого графика отразить от оси
, а затем все точки этого графика отразить от оси 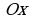 .
.
при a значения функции y = ax2 противоположны значениям функции y = -ax2 , следовательно, график функции y = ax2 получается из графика функции y = -аx2 отражением от оси Ох.
Свойства функции y = ax2 при a
Если x = 0, то y = 0.
График функции проходит через начало координат – вершина параболы.
Если x ≠ 0, то y
График функции расположен в нижней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) – убывает.
Функция принимает наибольшее значение, равно нулю, при x = 0.
Наименьшего значения функция не имеет, т. е. областью значений функции является промежуток (–∞; 0].
Ветви параболы направлены вниз;
Фокус параболы находится в точке 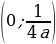 .
.
Графиком квадратичной функции y = ax2 при a



Задание.
На миллиметровой бумаге построить график функции 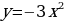 . По графику приближенно найти:
. По графику приближенно найти:
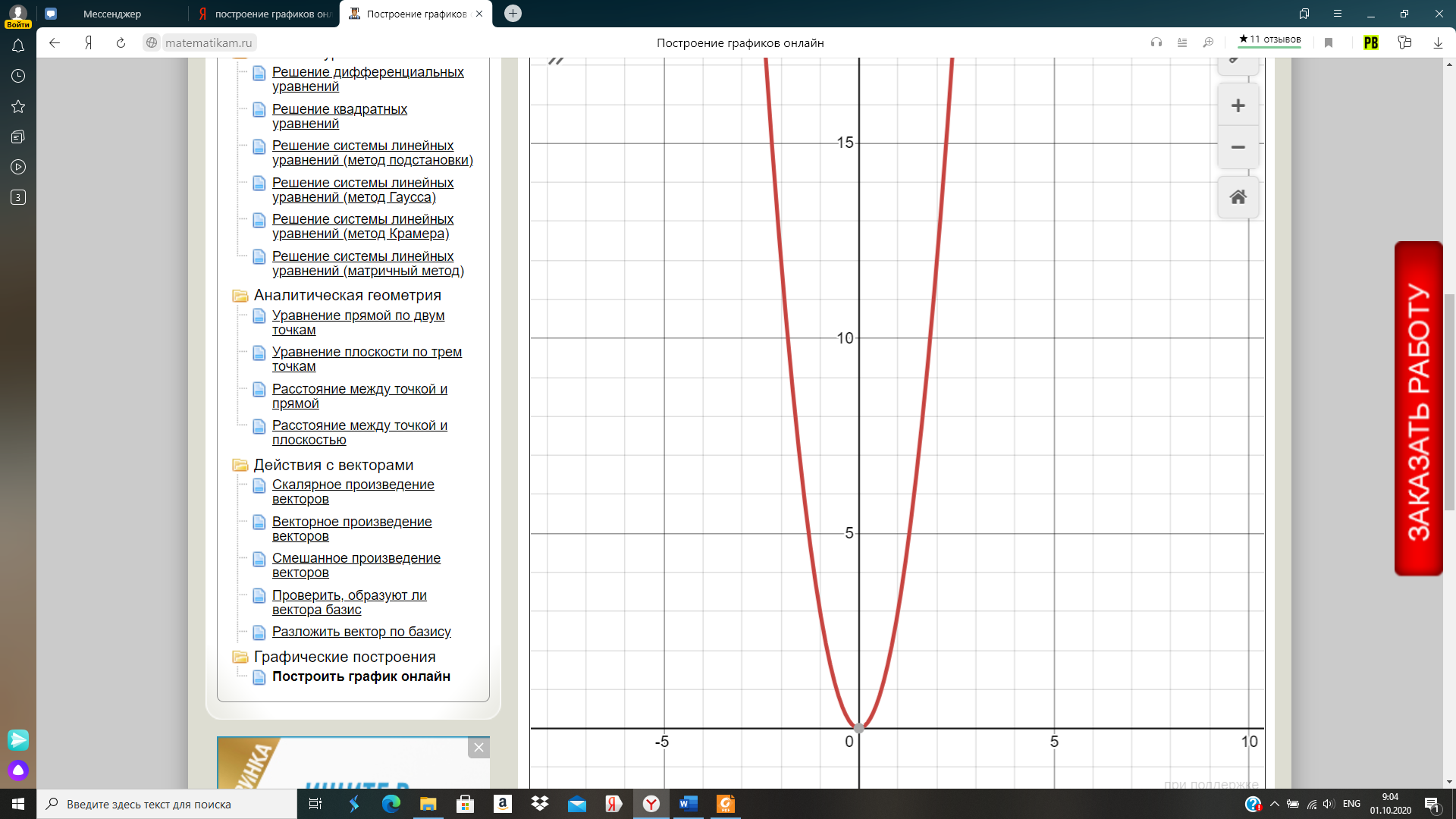
значения у при х=-2,8; -1,2; 1,5; 2,5;
значения х, если у=-9; -6; -8; -1,3.
Решение.
| x | -2 | -1 | 0 | 1 | 2 |
| y | -12 | -3 | 0 | -3 | -12 |
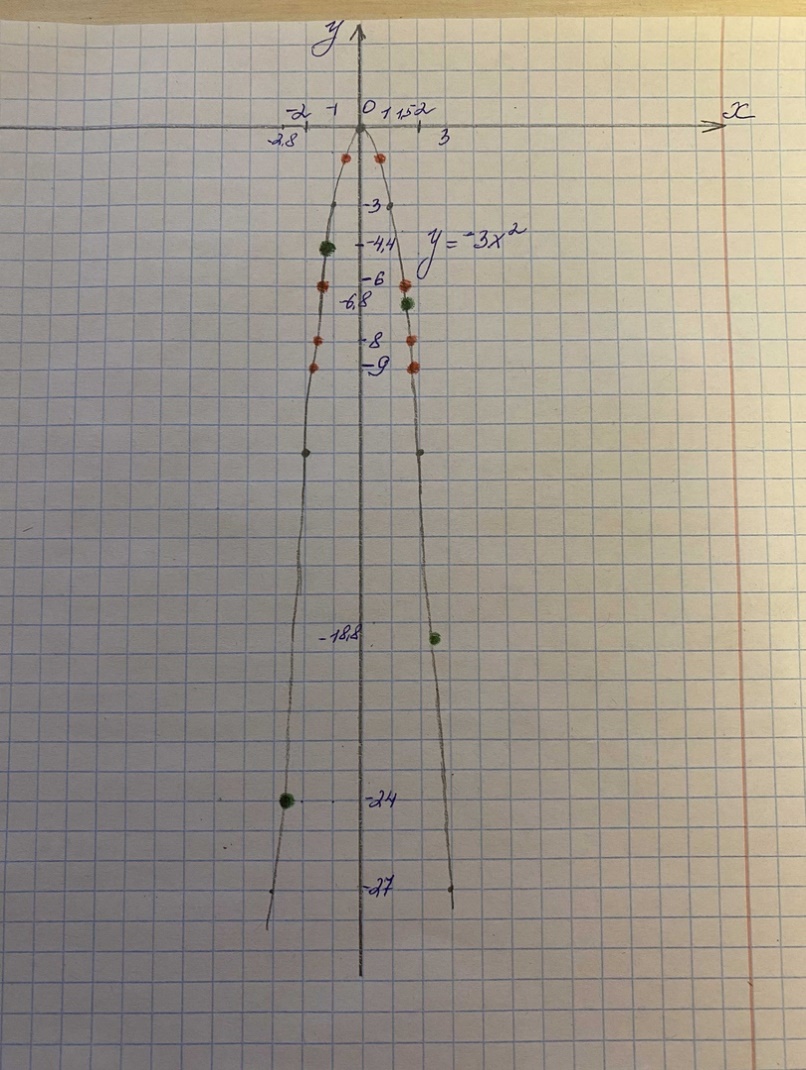
y(-2,8) ≈ -24
y(-1,2) ≈ -4,4
y(1,5) ≈ -6,8
y(2,5) ≈ -18,8
при у = -9 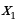 ≈ 1,7;
≈ 1,7; 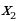 ≈ -1,7
≈ -1,7
при у = -6 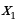 ≈ 1,4;
≈ 1,4; 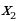 ≈ -1,4
≈ -1,4
при у =- 8 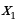 ≈ 1,6;
≈ 1,6; 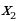 ≈ -1,6
≈ -1,6
при у = -1,3 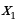 ≈ 0,6;
≈ 0,6; 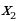 ≈ -0,6
≈ -0,6
4 Группа
Доклад на тему «Построение графика функции 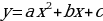 методом выделения полного квадрата»
методом выделения полного квадрата»
Пример 1.
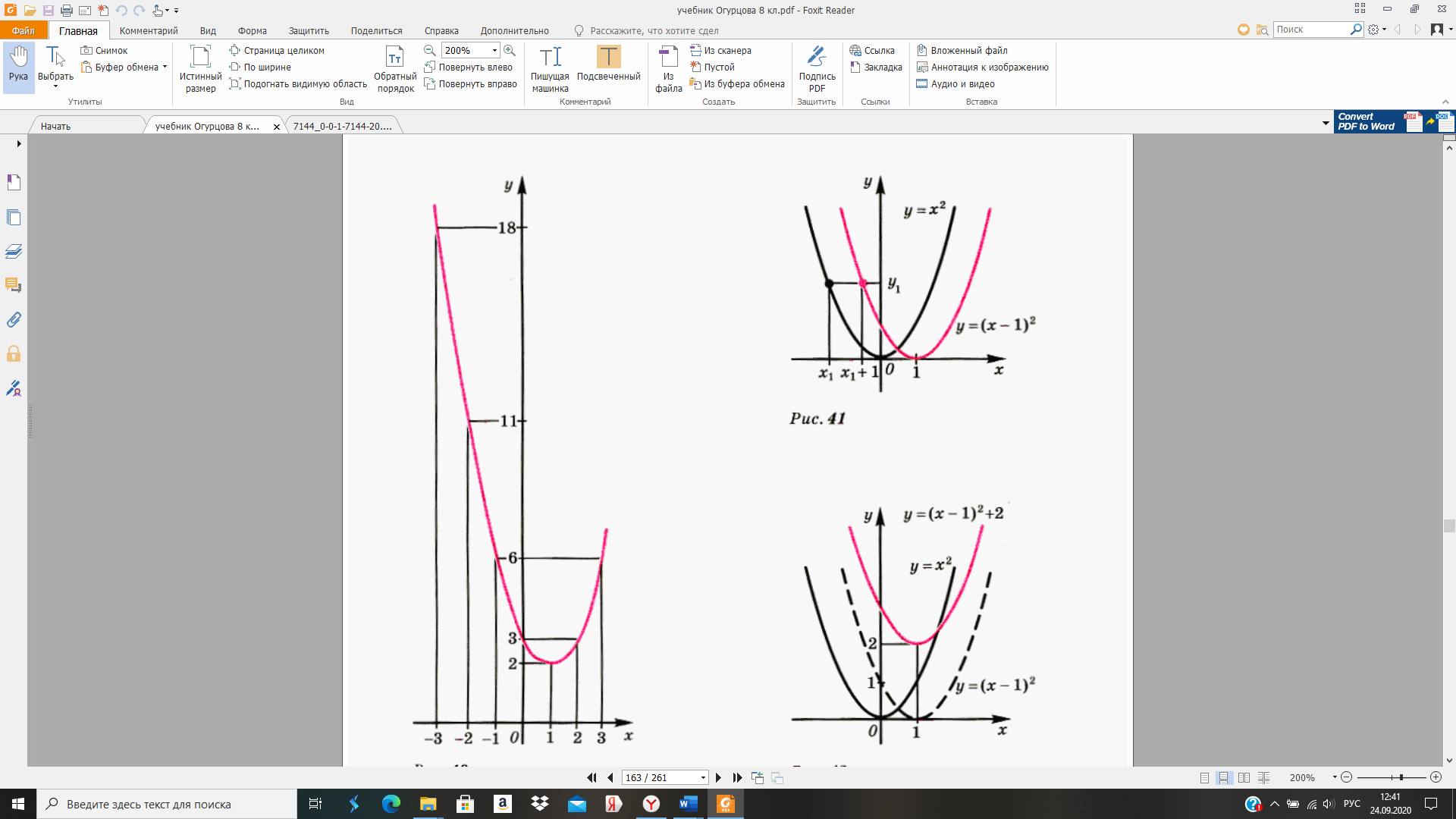
Построим график функции 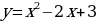
Составим таблицу:
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 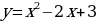
| 18 | 11 | 6 | 3 | 2 | 3 | 6 |
Построим найденные точки и проведем через них плавную кривую:
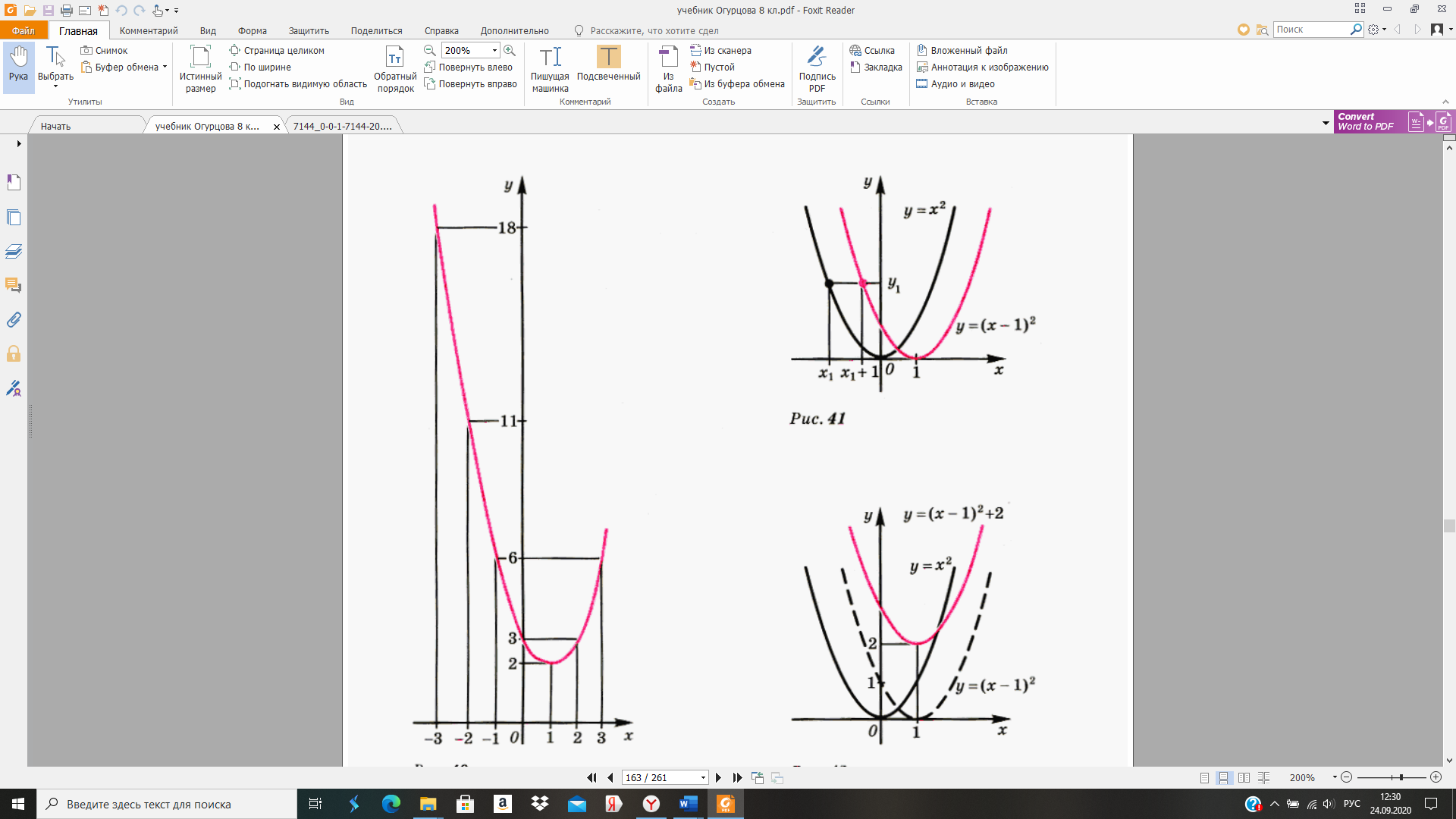
Преобразуем формулу, задающую функцию 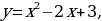 используя метод выделения полного квадрата:
используя метод выделения полного квадрата: 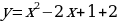 ,
, 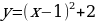 .
.
Видим, что тогда график функции 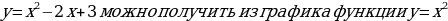 следующими преобразованиями:
следующими преобразованиями:
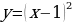 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 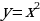 вправо на 1 единицу.
вправо на 1 единицу.
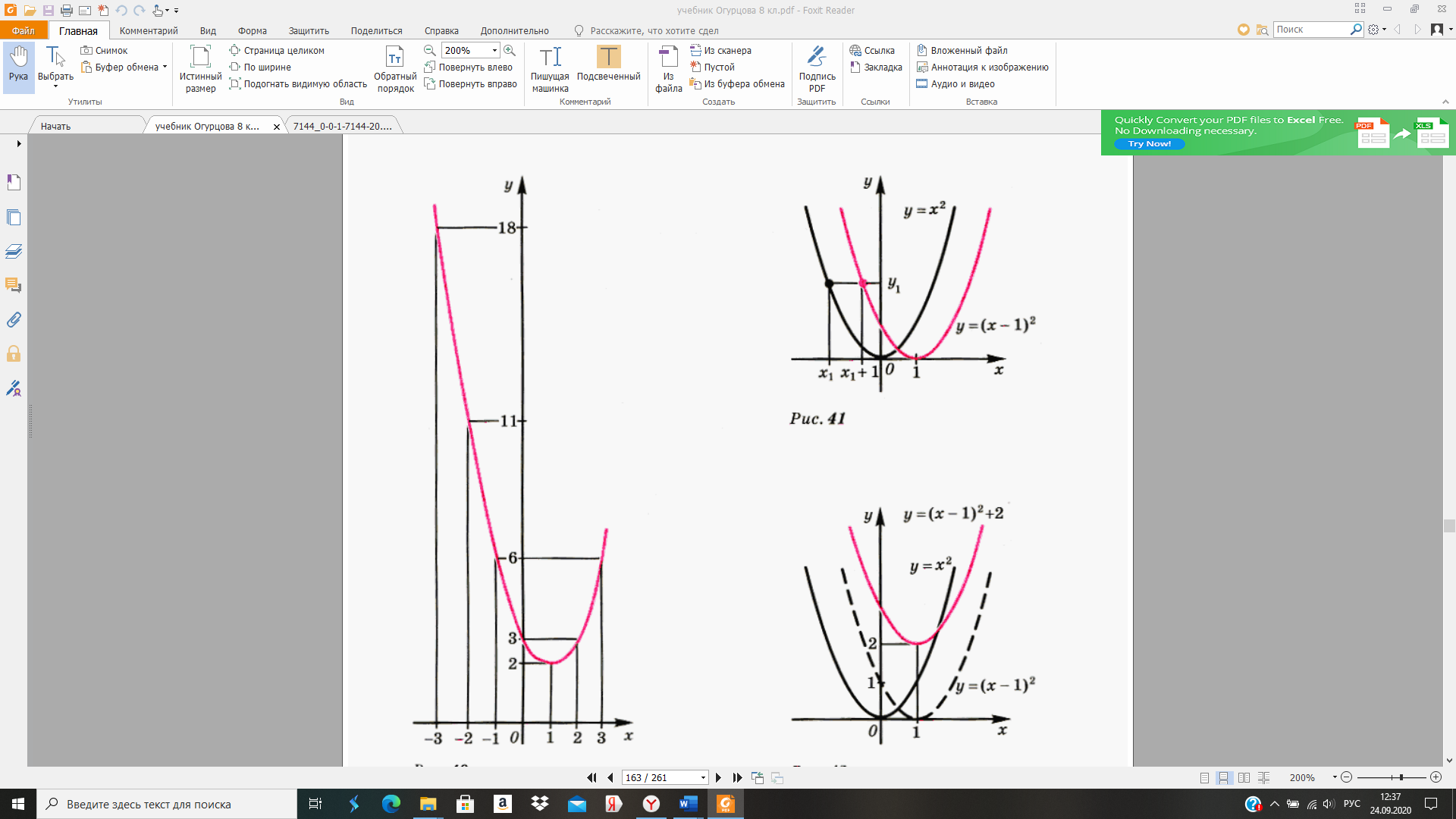
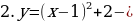 сдвиг (параллельный перенос)
сдвиг (параллельный перенос) 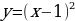 вверх на 2 единицы.
вверх на 2 единицы.
Пример 2.
Построим график функции 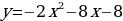 из графика функции
из графика функции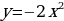 с помощью выделения полного квадрата.
с помощью выделения полного квадрата.
Преобразуем формулу: 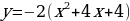 ,
, 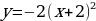 .
.
Видим, что тогда график функции 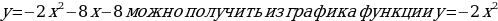 следующим преобразованием:
следующим преобразованием:
сдвиг (параллельный перенос) графика функции 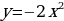 влево на 2 единицы.
влево на 2 единицы.
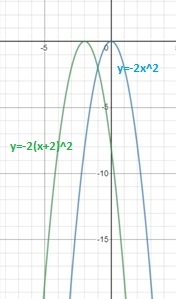
Итак, графиком функции 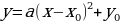 является парабола, получаемая сдвигом параболы
является парабола, получаемая сдвигом параболы 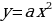 :
:
Любую квадратичную функцию 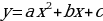 с помощью выделения полного квадрата можно записать в виде
с помощью выделения полного квадрата можно записать в виде 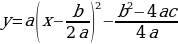 , т.е. в виде
, т.е. в виде 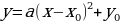 , где
, где 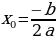 и
и 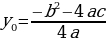 .
.
Таким образом, график функции y 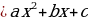 можно также назвать параболой.
можно также назвать параболой.
Если у квадратичной функции 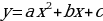
a0, то ветви параболы напрaвлены вверх;
a
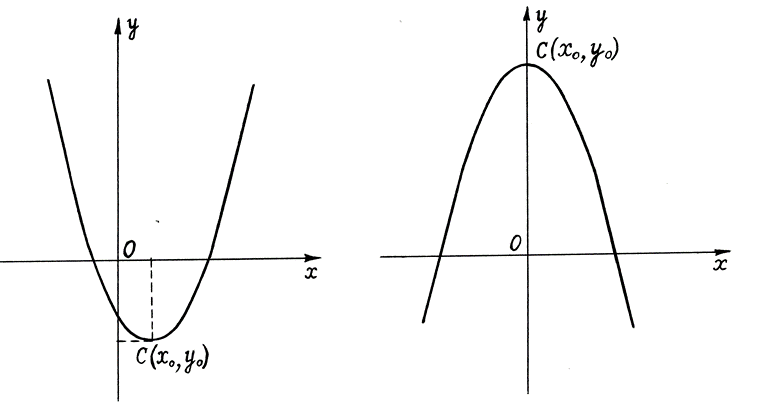
Итак, координаты (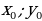 ) вершины параболы
) вершины параболы 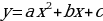 можно найти по формулам
можно найти по формулам 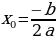 и
и 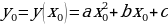 .
.
Если a0 , то в промежутке (–∞;  ] функция
] функция 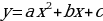 убывает, а в промежутке [
убывает, а в промежутке [ ; +∞) - возрастает.
; +∞) - возрастает.
Если a, то в промежутке (–∞;  ] функция
] функция 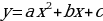 возрастает, а в промежутке [
возрастает, а в промежутке [ ; +∞) - убывает.
; +∞) - убывает.
Областью значений квадратичной функции 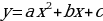 является промежуток :
является промежуток :
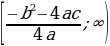 , если а0
, если а0
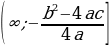 , если а
, если а
Ось симметрии параболы 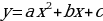 – прямая, параллельная оси ординат и проходящая через вершину параболы.
– прямая, параллельная оси ординат и проходящая через вершину параболы.
Квадратичные функции часто встречаются в различных областях науки и техники. Например, если тело брошено вверх со скоростью υ, то расстояние s от него до поверхности земли в момент времени t определяется формулой 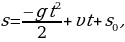 где
где 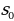 – расстояние от тела до поверхности земли в момент времени t=0.
– расстояние от тела до поверхности земли в момент времени t=0.
Также квадратичные функции появляются при решении задач.
Задача: Одна сторона прямоугольника больше другой на 10 см Выразите площадь прямоугольника.
Выразите площадь прямоугольника.
Пусть х сантиметров – высота прямоугольника, тогда его основание равно (х+10) сантиметров. Площадь этого прямоугольника равна х(х+10)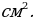
Раскрывая скобки, получаем:
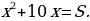
Задание: № 624(3,4)
№ 624(3,4)
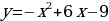
Преобразуем формулу: 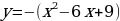
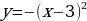
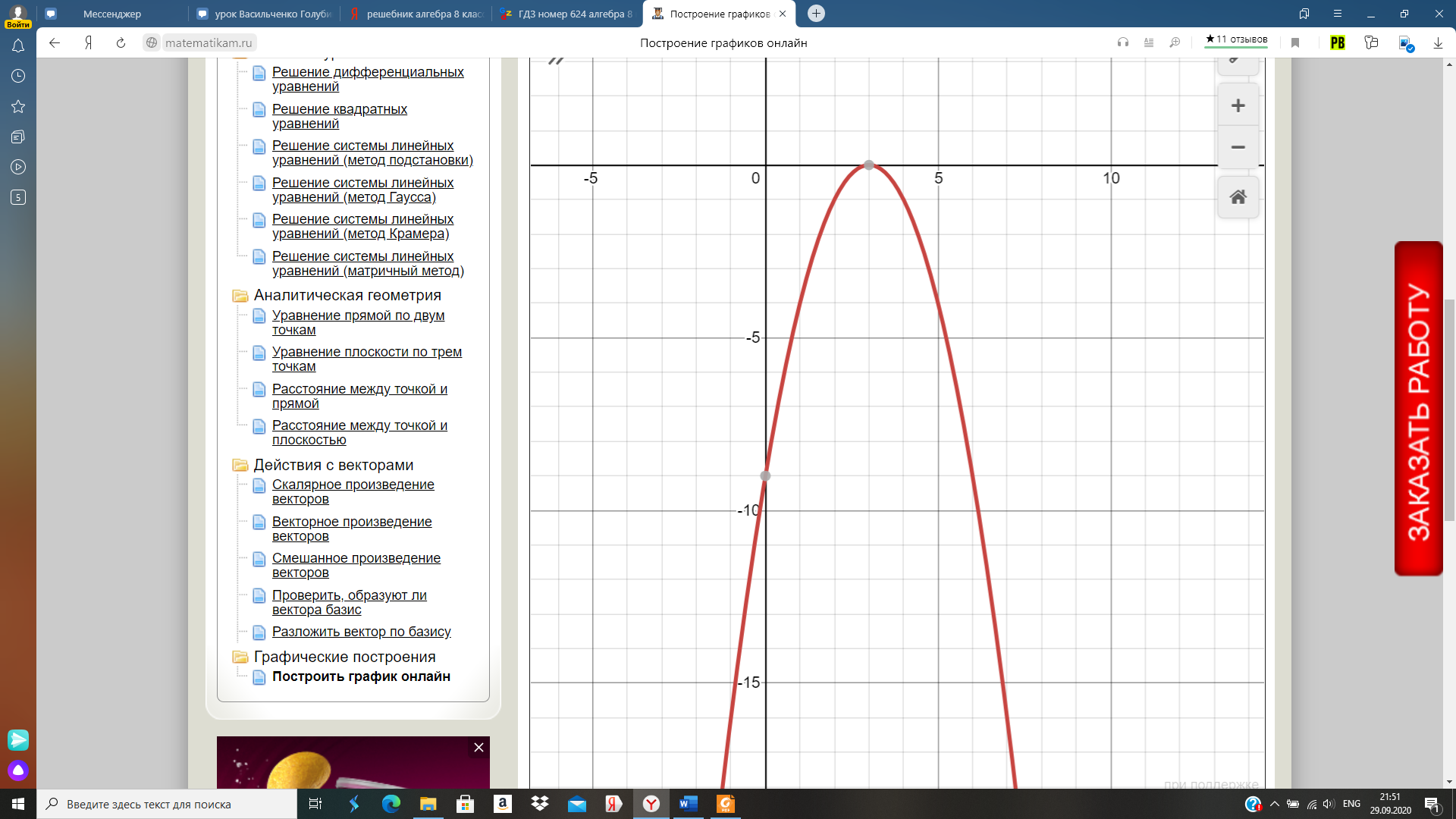
Видим, что тогда график функции 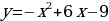
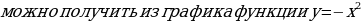 следующими преобразованием:
следующими преобразованием:
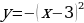 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 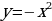 вправо на 3 единицы.
вправо на 3 единицы.
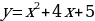
Преобразуем формулу: 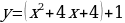 ,
, 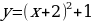 .
.
Видим, что тогда график функции 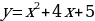
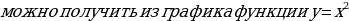 следующим преобразованиями:
следующим преобразованиями:
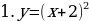 сдвиг (параллельный перенос) графика функции
сдвиг (параллельный перенос) графика функции 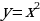 влево на 2 единицы;
влево на 2 единицы;
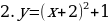 сдвиг (параллельный перенос) графика функции
сдвиг (параллельный перенос) графика функции 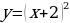 вверх на 1 единицы
вверх на 1 единицы
Группа 5
Доклад на тему «Построение графика функции y =ax2+bx+c с помощью алгоритма»
Исходя из предыдущих докладов мы можем сделать вывод, что график любой квадратичной функции y=a +bx+c можно построить по следующему алгоритму:
+bx+c можно построить по следующему алгоритму:
Построить вершину параболы ( ;
;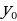 ), вычислив
), вычислив  по формулам
по формулам  =-
=-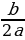
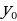 =y(
=y(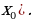
Провести через вершину параболы прямую, параллельную оси ординат, - оси симметрии параболы.
Найти нули функции, если они есть, и построить на оси абсцисс соответствующие точки параболы.
Построить две какие-нибудь точки параболы, симметричные относительно ее оси. Для этого надо взять две точки на оси Ox, симметричные относительно точки  , и вычислить соответствующие значения функции (эти значения одинаковы). Например, можно построить точки параболы с абсциссами x=0 и x=2
, и вычислить соответствующие значения функции (эти значения одинаковы). Например, можно построить точки параболы с абсциссами x=0 и x=2 , если
, если  ≠0 (ординаты этих точек равны c).
≠0 (ординаты этих точек равны c).
Провести через построенные точки параболу. Заметим, что для более точного построения графика полезно найти еще несколько точек параболы.
Пример 1. Построим график функции y= -4x+3.
-4x+3.
Найдем координаты вершины параболы:
 =-
=-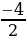 =2;
=2; 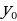 =
=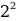 -7*2+10=-1.
-7*2+10=-1.
Построим точку (2;-1).
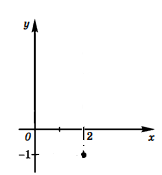
Проведем через точку (2;-1) прямую, параллельную оси ординат – ось симметрии параболы.
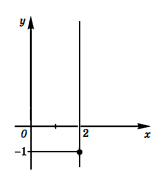
Решая уравнение  -4x+3=0, найдем нули функции:
-4x+3=0, найдем нули функции: 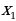 =1,
=1, 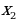 =3. Построим точки (1;0) и (3;0).
=3. Построим точки (1;0) и (3;0).
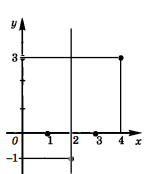
Возьмем две точки на оси Ox, симметричные относительно точки x=2, например, точки x=0 и x=4. Вычислим значение функции в этих точках: y(0)=y(4)=3. Построим точки (0;3) и (4;3)
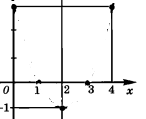
Проведем параболу через построенные точки.
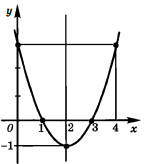
Итак, мы построили график квадратичной функции, не выделяя при этом полный квадрат.
Пример 2. Построить график функции y=-2 +3x+2.
+3x+2.
Найдем координаты вершины параболы:
 =-
=-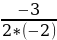 =
=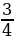 ;
; 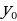 =-2*
=-2*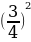 +3*
+3*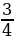 +2=3
+2=3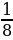 .
.
Построим точку (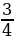 ;3
;3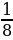 ).
).
Проведем через точку (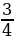 ;3
;3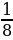 ) прямую, параллельную оси ординат – ось симметрии параболы.
) прямую, параллельную оси ординат – ось симметрии параболы.
Решая уравнение -2 +3x+2=0, найдем нули функции:
+3x+2=0, найдем нули функции: 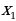 =2,
=2, 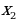 =-
=- . Построим точки (2;0) и (-
. Построим точки (2;0) и (- ;0).
;0).
Возьмем две точки на оси Ox, симметричные относительно точки x=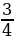 , например, точки x=0 и x=1
, например, точки x=0 и x=1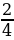 . Вычислим значение функции в этих точках: y(0)=y(1
. Вычислим значение функции в этих точках: y(0)=y(1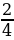 )=2. Построим точки (0;2) и (1
)=2. Построим точки (0;2) и (1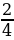 ;2)
;2)
Проведем параболу через построенные точки.
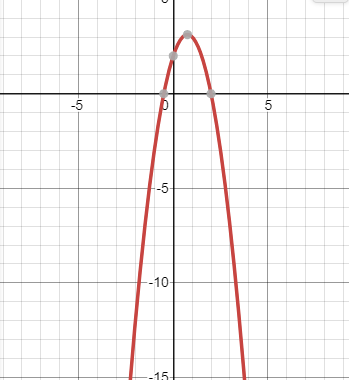
Приведем примеры практических заданий, в которых используются свойства квадратичной функции.
Для начала вспомним свойства, которые нам понадобятся:
Функция y =ax2+bx+c принимает наименьшее или наибольшее значение в точке  =-
=-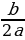 , которая является вершиной параболы.
, которая является вершиной параболы.
При этом, если a0, то функция имеет наименьшее значение, а если a, то функция имеет наибольшее значение.
Пр.з.1. Число 15 представить в виде суммы двух чисел так, чтобы произведение этих чисел было наибольшим.
Решение, Пусть x и (15-x) – данные числа. Тогда их произведение x(15-x) должно быть наибольшим.
Рассмотрим функцию y=x(15-x), y=- +15x – квадратичная функция, график – парабола.
+15x – квадратичная функция, график – парабола.
a=-1  =-
=-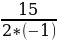 =
=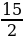 = 7,5
= 7,5
Итак, 7,5 – первое число, тогда 15-7,5 = 7,5 – второе число.
Ответ: Эти числа 7,5 и 7,5.
Пр.з.2. Сумма двух чисел равна 10. Найти эти числа, если сумма их кубов является наименьшей.
Решение. Пусть x и (10-x) – искомые числа. Тогда сумма их кубов:
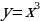 +
+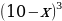 , у=
, у=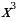 +(1000-3*100x+3*10
+(1000-3*100x+3*10 -
-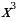 ), у=
), у=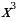 +1000-300x+30
+1000-300x+30 -
-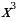 , у=30
, у=30 -300x+1000 – квадратичная функция, график – парабола.
-300x+1000 – квадратичная функция, график – парабола.
a=301, значит, ветви параболы направлены вверх, и наименьшее значение парабола принимает в ее вершине.
 =-
=-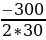 =5.
=5.
Итак, первое число – 5, тогда второе 10-5=5.
Ответ: Эти числа 5 и 5.
Номера из учебника: №624(1,2), 625(2,4).
Решение:
№624:
1) y= -7x+10.
-7x+10.
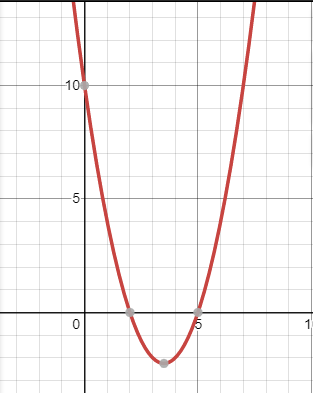
y0 при x5
yпри 2
y возрастает при x3,5
y убывает при x
a=10, значит функция принимает наименьшее значение в своей вершине, то есть при  =-
=-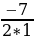 =3,5.
=3,5.
2) y=- +x+2.
+x+2.
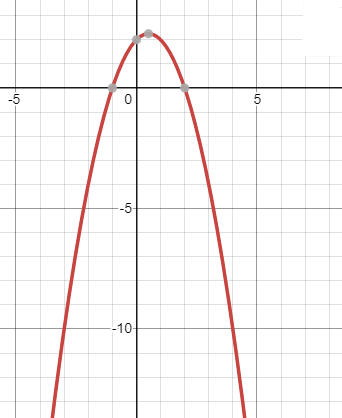
y0 при -1
yпри x2
y возрастает при x
y убывает при x0,5
a=-1 =-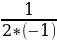 =0,5.
=0,5.
№625:
2) y=-3 -2x+1.
-2x+1.
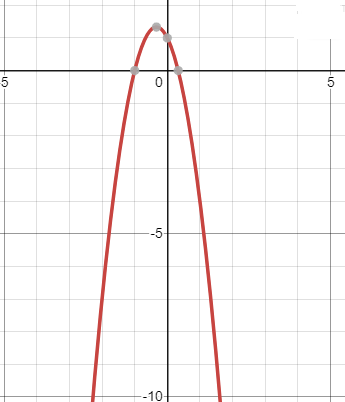
yпри x
yпри -1
y возрастает при x
y убывает при x-
a=-3 =-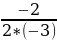 =-
=- .
.
4) y=3 -8x+4.
-8x+4.
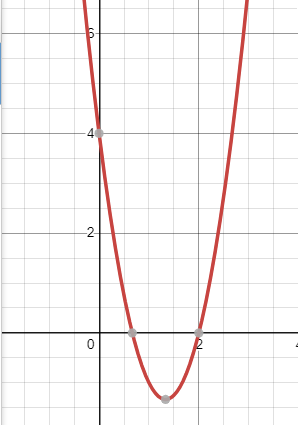
yпри 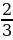
y0 при x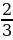 , x2
, x2
y возрастает при x1
y убывает при x
a=30, значит функция принимает наименьшее значение в своей вершине, то есть при  =-
=-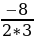 =1
=1 .
.
3. Рефлексивно-оценочная часть
-Какова была цель нашего урока? (Изучить в процессе докладов учащихся построение графиков функций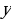 =
=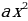 и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐)
и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐)
-Достигли ли мы данной цели? (Да)
РЕФЕРАТЫ
Реферат первой группы на тему «График функции 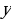 =
=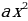 при
при 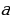 1 и её свойства»
1 и её свойства»
Пример 1.
Построим график функции y = 2x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 2x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2x2 | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = 2x2 больше значений функции y = x2 в 2 раза. Графически это означает, что график функции y = 2x2 получается растяжением графика функции y = x2 от оси Ох вдоль оси Оу в 2 раза.

Пример 2.
Построим график функции y = 2,5x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 2,5x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2,5x2 | 22,5 | 10 | 2,5 | 0 | 2,5 | 10 | 22,5 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = 2,5x2 больше значений функции y = x2 в 2,5 раза. Графически это означает, что график функции y = 2,5x2 получается растяжением графика функции y = x2 от оси Ох вдоль оси Оу в 2,5 раза.

Пример 3.
Построим график функции y = 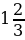 x2 и сравним его с графиком функции y = x2.
x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 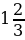 x2 или y =
x2 или y = 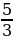 x2
x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 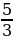 x2 x2 | 15 | 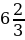
| 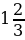 | 0 | 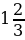
| 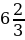
| 15 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = 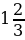 x2 больше значений функции y = x2 в
x2 больше значений функции y = x2 в 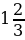 раза. Графически это означает, что график функции y =
раза. Графически это означает, что график функции y = 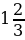 x2 получается растяжением графика функции y = x2 от оси Ох вдоль оси Оу в
x2 получается растяжением графика функции y = x2 от оси Ох вдоль оси Оу в 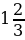 раза.
раза.
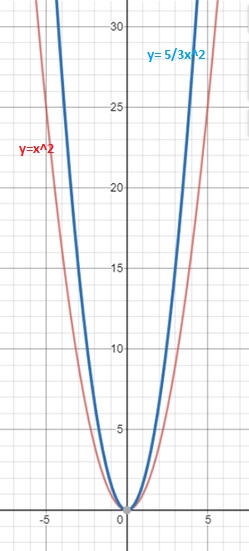
Таким образом, график функции y = ax2 при любом a1 можно также назвать параболой.
При a1 значения функции y = ax2 больше значений функции y = x2 в а раз, следовательно, график функции y = ax2 получается из графика функции y = x2 растяжением его в а раз от оси Ох вдоль оси Оу.
Свойства функции y = ax2 при a 1:
1. Если x = 0, то y = 0.
График функции проходит через начало координат – вершина параболы.
2. Если x ≠ 0, то y 0.
График функции расположен в верхней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает.
5. Функция принимает наименьшее значение, равно нулю, при x = 0.
6. Наибольшего значения функция не имеет, т.е. областью значений функции является промежуток [0; +∞).
7. Ветви параболы направлены вверх.
8. Фокус параболы находится в точке 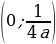 .
.
Квадратичная функция y = ax2 играет большую роль в познании реального мира. Рассмотрим несколько примеров парабол.
В физике можно рассмотреть следующие зависимости:
- мощности электрического тока P=I2R при постоянном сопротивлении,
- кинетической энергии E=mv2/2 при постоянной массе.
В природе встречается данный вид квадратичной функции, например, горы задают именно такую функцию.

Другой пример:

№ 595
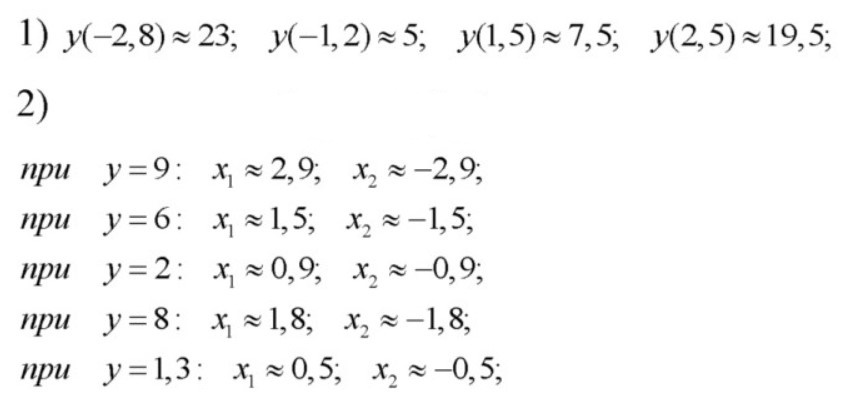

Реферат второй группы на тему
«График функции 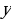 =
=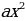 при
при 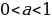 и её свойства»
и её свойства»
Пример 1.
Построим график функции y =  x2 и сравним его с графиком функции y = x2.
x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y =  x2
x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y =  x2 x2 | 4,5 | 2 | 0,5 | 0 | 0,5 | 2 | 4,5 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y =  x2 меньше значений функции y = x2 в 2 раза. Графически это означает, что график функции y =
x2 меньше значений функции y = x2 в 2 раза. Графически это означает, что график функции y =  x2 получается сжатием графика функции y=
x2 получается сжатием графика функции y= вдоль оси Oy к оси Ox в 2 раза.
вдоль оси Oy к оси Ox в 2 раза.
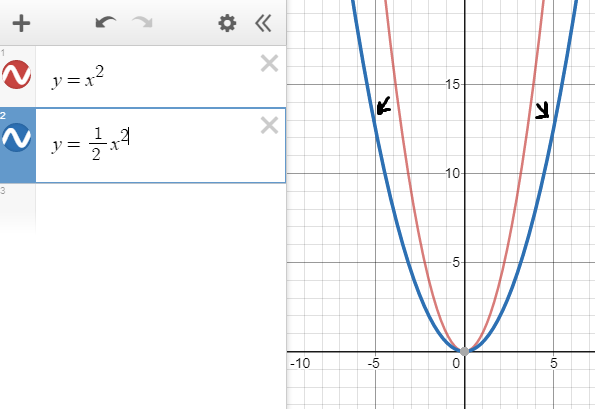
Пример 2.
Построим график функции y = 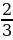 x2 и сравним его с графиком функции y = x2.
x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 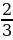 x2
x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 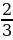 x2 x2 | 6 | 2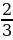 | 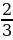
| 0 | 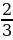
| 2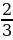 | 6 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y =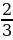 x2 меньше значений функции y = x2в
x2 меньше значений функции y = x2в 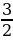 раза. Графически это означает, что график функции y =
раза. Графически это означает, что график функции y = 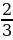 x2 получается сжатием графика функции y=
x2 получается сжатием графика функции y= вдоль оси Oy к оси Ox в
вдоль оси Oy к оси Ox в 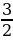 раза
раза
Пример 3.
Построим график функции y = 0,2x2 и сравним его с графиком функции y = x2.
Составим таблицу значений функции y = x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Также составим таблицу значений функции y = 0,2x2
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 0,2x2 | 1,8 | 0,8 | 0,2 | 0 | 0,2 | 0,8 | 1,8 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y =0,2x2 меньше значений функции y = x2 в 5 раз. Графически это означает, что график функции y = 0,2 x2 получается сжатием графика функции y= вдоль оси Oy к оси Ox в 5 раз.
вдоль оси Oy к оси Ox в 5 раз.
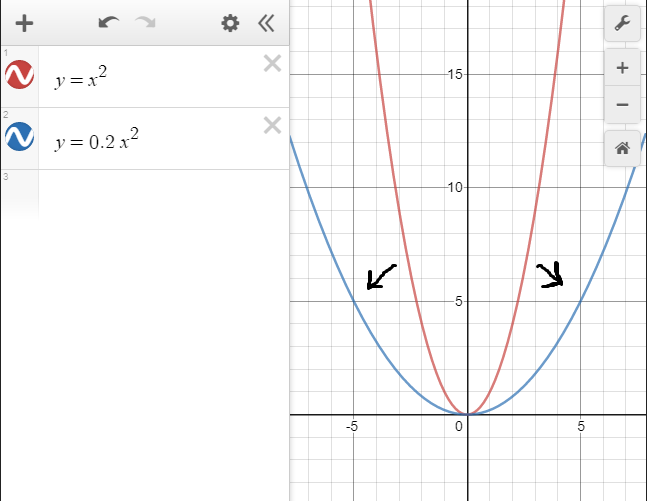
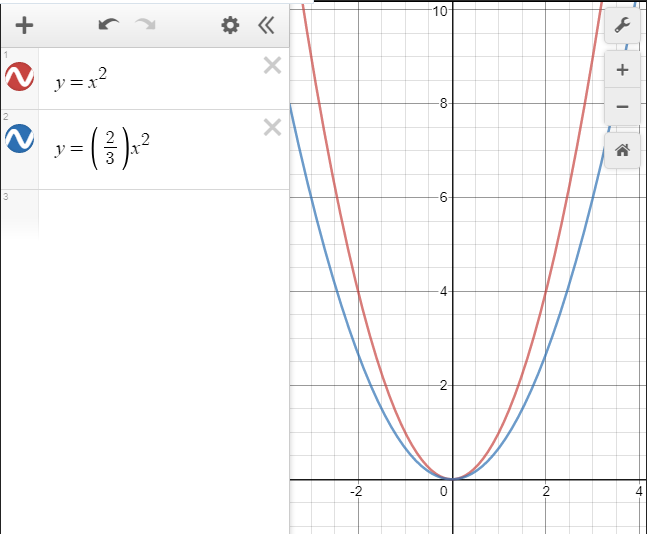
Таким образом, график функции y = ax2 при любом 0a можно также назвать параболой.
При 0a значения функции y = ax2 меньше значений функции y = x2 в 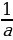 раз, следовательно, график функции y = ax2 получается из графика функции y = x2 сжатием его в
раз, следовательно, график функции y = ax2 получается из графика функции y = x2 сжатием его в 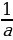 раз к оси Ох вдоль оси Оу.
раз к оси Ох вдоль оси Оу.
Свойства функции y = ax2 при 0a
1. Если x = 0, то y = 0.
График функции проходит через начало координат – вершина параболы.
2. Если x ≠ 0, то y 0.
График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает.
5. Функция принимает наименьшее значение, равно нулю, при x = 0.
6. Наибольшего значения функция не имеет, т.е. областью значений функции является промежуток [0; +∞).
7. Ветви параболы направлены вверх.
8. Фокус параболы находится в точке 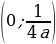 .
.
График квадратичной функции – парабола - довольно часто встречается в окружающей действительности. Например, это можно наблюдать в рампах, которые строятся для велосипедистов и скейтбордистов, а также в спутниковых тарелках.



Другой пример:

Задание: Постройте на милиметровой бумаге график функции y=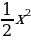 . По графику приближенно найти:
. По графику приближенно найти:
1) значения y, при x= -1; -1,2; -4; 2; -2,5.
2) значения x, если y= 1; 8; 2; 6; 2,25.
Решение:

y(-1)=0,5
y(-1,2)≈0,7
y(-4)=8
y(2)=2
y(-2,5)=3
при y=1 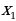 =-1,5,
=-1,5, 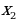 =1,5
=1,5
при y=8 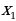 =-4,
=-4, 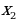 =4
=4
при y=2 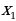 =-2,
=-2, 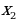 =2
=2
при y=6 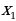 =-3,5,
=-3,5, 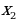 =3,5
=3,5
при y=2,25 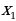 ≈-2,1,
≈-2,1, 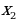 ≈2,1
≈2,1
Реферат 3 группы
«График функции 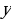 =
=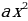 при a и её свойства»
при a и её свойства»
Пример 1. Построим график функции 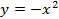 и сравним его с графиком функции y = x2.
и сравним его с графиком функции y = x2.
Составим таблицу значений функции y= .
.
| х | -1 | 0 | 1 | 2 |
| y = x2 | 1 | 0 | 1 | 4 |
Также составим таблицу значений функции y=−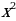
| х | -1 | 0 | 1 | 2 |
| y = x2 | -1 | 0 | -1 | -4 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = - x2 противоположны значениям функции y = x2. Графически это означает, что график функции y = - x2 получается отражением из графика функции y= от оси Ox
от оси Ox

Пример 2. Построить график функции 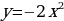 и сравним его с графиком функции y = 2x2.
и сравним его с графиком функции y = 2x2.
Составим таблицу значений функции y=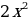 .
.
Также составим таблицу значений функции y=−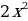
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = - 2 x2 противоположны значениям функции y = 2 x2 . Графически это означает, что график функции y = - 2 x2 получается отражением из графика функции y=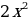 от оси Ox
от оси Ox

Пример 3. Построить график функции 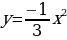 и сравним его с графиком функции y =
и сравним его с графиком функции y =  x2.
x2.
Составим таблицу значений функции 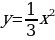 .
.
| х | 6 | 3 | 1 | 0 | -1 | -3 | -6 |
| 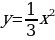
| 12 | 3 | 
| 0 | 
| 3 | 12 |
Также составим таблицу значений функции 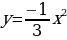
| х | 6 | 3 | 1 | 0 | -1 | -3 | -6 |
| 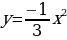
| -12 | -3 | - | 0 | 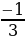
| -3 | -12 |
Из таблиц видно, что при одних и тех же значениях аргумента значения функции y = 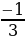 x2 противоположны значениям функции y =
x2 противоположны значениям функции y =  x2. Графически это означает, что график функции y =
x2. Графически это означает, что график функции y = 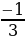 x2 получается отражением из графика функции y=
x2 получается отражением из графика функции y=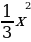 от оси Ox
от оси Ox
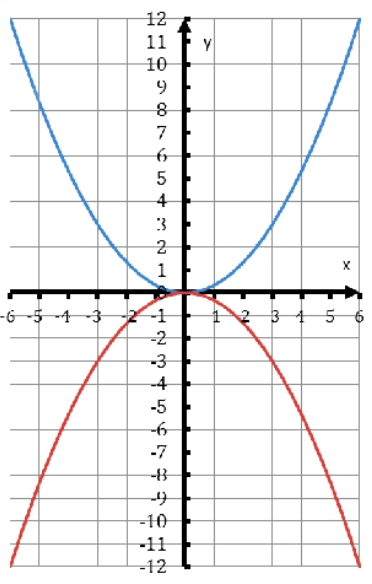
Таким образом, график функции y = ax2 при любом a можно также назвать параболой.
Известно, что чтобы построить график функции 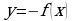 , надо построить график функции
, надо построить график функции 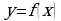 , а затем все точки этого графика отразить от оси
, а затем все точки этого графика отразить от оси 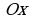 .
.
К указанному выводу легко прийти, сравнивая значения функций 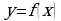 и
и 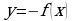 при одних и тех же значениях аргумента.
при одних и тех же значениях аргумента.
Легко доказывается, что при симметрии относительно оси 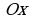 образ любой точки
образ любой точки 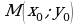 , принадлежащей графику функции
, принадлежащей графику функции 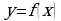 , есть точка
, есть точка 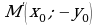 , принадлежащая графику функции
, принадлежащая графику функции 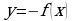 , а также обратно.
, а также обратно.
Итак. при a значения функции y = ax2 противоположны значениям функции y = -ax2 , следовательно, график функции y = ax2 получается из графика функции y = -аx2 отражением от оси Ох.
Свойства функции y = ax2 при a
Если x = 0, то y = 0.
График функции проходит через начало координат – вершина параболы.
Если x ≠ 0, то y
График функции расположен в нижней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции.
График функции представляет собой симметричную фигуру относительно оси y.
В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) – убывает.
Функция принимает наибольшее значение, равно нулю, при x = 0.
Наименьшего значения функция не имеет, т. е. областью значений функции является промежуток (–∞; 0].
Ветви параболы направлены вниз;
Фокус параболы находится в точке 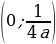 .
.
Графиком квадратичной функции y = ax2 при a




Задание.
На миллиметровой бумаге построить график функции 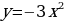 . По графику приближенно найти:
. По графику приближенно найти:
значения у при х=-2,8; -1,2; 1,5; 2,5;
значения х, если у=-9; -6; -8; -1,3.
Решение.
| x | -2 | -1 | 0 | 1 | 2 |
| y | -12 | -3 | 0 | -3 | -12 |

y(-2,8) ≈ -24
y(-1,2) ≈ -4,4
y(1,5) ≈ -6,8
y(2,5) ≈ -18,8
при у = -9 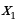 ≈ 1,7;
≈ 1,7; 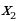 ≈ -1,7
≈ -1,7
при у = -6 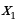 ≈ 1,4;
≈ 1,4; 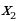 ≈ -1,4
≈ -1,4
при у =- 8 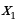 ≈ 1,6;
≈ 1,6; 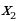 ≈ -1,6
≈ -1,6
при у = -1,3 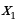 ≈ 0,6;
≈ 0,6; 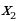 ≈ -0,6
≈ -0,6
Реферат 4 группы
«Построение графика функции 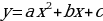 методом выделения полного квадрата»
методом выделения полного квадрата»
Пример 1.
Построим график функции 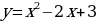
Составим таблицу:
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 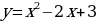
| 18 | 11 | 6 | 3 | 2 | 3 | 6 |
Построим найденные точки и проведем через них плавную кривую:

Преобразуем формулу, задающую функцию 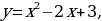 используя метод выделения полного квадрата:
используя метод выделения полного квадрата: 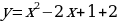 ,
, 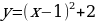 .
.
Видим, что тогда график функции 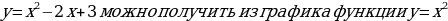 следующими преобразованиями:
следующими преобразованиями:
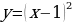 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 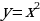 вправо на 1 единицу.
вправо на 1 единицу.

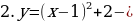 сдвиг (параллельный перенос)
сдвиг (параллельный перенос) 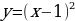 вверх на 2 единицы.
вверх на 2 единицы.

Пример 2.
Построим график функции 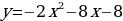 из графика функции
из графика функции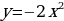 с помощью выделения полного квадрата.
с помощью выделения полного квадрата.
Преобразуем формулу: 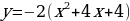 ,
, 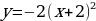 .
.
Видим, что тогда график функции 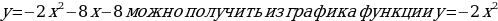 следующим преобразованием:
следующим преобразованием:
сдвиг (параллельный перенос) графика функции 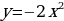 влево на 2 единицы.
влево на 2 единицы.

Пример 3.
Построим график функции 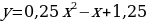 из графика функции
из графика функции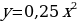 с помощью выделения полного квадрата.
с помощью выделения полного квадрата.
Преобразуем формулу: 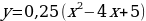 ,
, 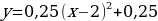 .
.
Видим, что тогда график функции 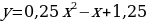
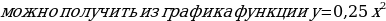 следующими преобразованиями:
следующими преобразованиями:
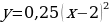 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 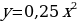 вправо на 2 единицы.
вправо на 2 единицы.
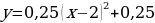 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 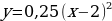 вверх на 0,25 единиц.
вверх на 0,25 единиц.
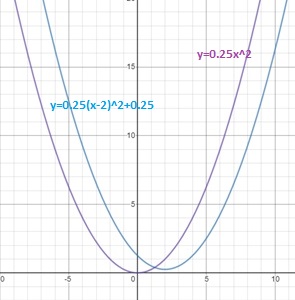
Итак, графиком функции 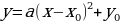 является парабола, получаемая сдвигом параболы
является парабола, получаемая сдвигом параболы 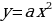 :
:
Любую квадратичную функцию 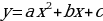 с помощью выделения полного квадрата можно записать в виде
с помощью выделения полного квадрата можно записать в виде 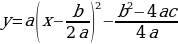 , т.е. в виде
, т.е. в виде 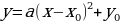 , где
, где 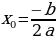 и
и 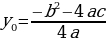 .
.
Таким образом, график функции y 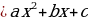 можно также назвать параболой.
можно также назвать параболой.
Если у квадратичной функции 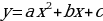
a0, то ветви параболы напрaвлены вверх;
a
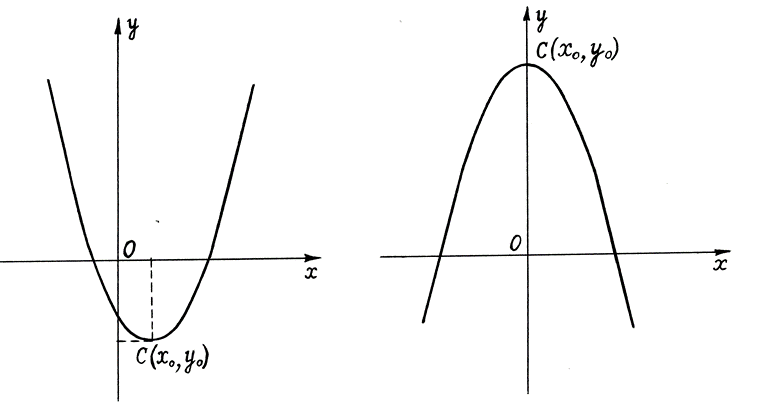
Итак, координаты (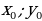 ) вершины параболы
) вершины параболы 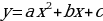 можно найти по формулам
можно найти по формулам 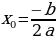 и
и 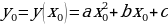 .
.
Если a0 , то в промежутке (–∞;  ] функция
] функция 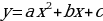 убывает, а в промежутке [
убывает, а в промежутке [ ; +∞) - возрастает.
; +∞) - возрастает.
Если a, то в промежутке (–∞;  ] функция
] функция 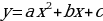 возрастает, а в промежутке [
возрастает, а в промежутке [ ; +∞) - убывает.
; +∞) - убывает.
Областью значений квадратичной функции 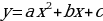 является промежуток :
является промежуток :
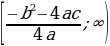 , если а0
, если а0
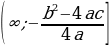 , если а
, если а
Ось симметрии параболы 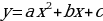 – прямая, параллельная оси ординат и проходящая через вершину параболы.
– прямая, параллельная оси ординат и проходящая через вершину параболы.
Квадратичные функции часто встречаются в различных областях науки и техники. Например, если тело брошено вверх со скоростью υ, то расстояние s от него до поверхности земли в момент времени t определяется формулой 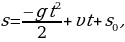 где
где 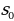 – расстояние от тела до поверхности земли в момент времени t=0.
– расстояние от тела до поверхности земли в момент времени t=0.
Также квадратичные функции появляются при решении задач.
Задача: Одна сторона прямоугольника больше другой на 10 см Выразите площадь прямоугольника.
Выразите площадь прямоугольника.
Пусть х сантиметров – высота прямоугольника, тогда его основание равно (х+10) сантиметров. Площадь этого прямоугольника равна х(х+10)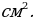
Раскрывая скобки, получаем:
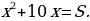
Задание: № 624(3,4)
№ 624(3,4)
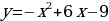
Преобразуем формулу: 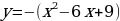
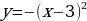
Видим, что тогда график функции 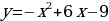
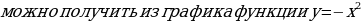 следующими преобразованием:
следующими преобразованием:
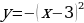 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 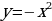 вправо на 3 единицы.
вправо на 3 единицы.

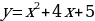
Преобразуем формулу: 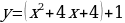 ,
, 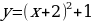 .
.
Видим, что тогда график функции 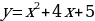
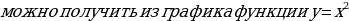 следующим преобразованиями:
следующим преобразованиями:
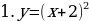 сдвиг (параллельный перенос) графика функции
сдвиг (параллельный перенос) графика функции 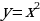 влево на 2 единицы;
влево на 2 единицы;
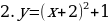 сдвиг (параллельный перенос) графика функции
сдвиг (параллельный перенос) графика функции 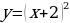 вверх на 1 единицы
вверх на 1 единицы

Реферат 5 группы
Доклад на тему: «Построение графика функции y =ax2+bx+c с помощью алгоритма»
Исходя из предыдущих докладов мы можем сделать вывод, что график любой квадратичной функции y=a +bx+c можно построить по следующему алгоритму:
+bx+c можно построить по следующему алгоритму:
Построить вершину параболы ( ;
;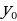 ), вычислив
), вычислив  по формулам
по формулам  =-
=-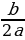
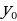 =y(
=y(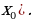
Провести через вершину параболы прямую, параллельную оси ординат, - оси симметрии параболы.
Найти нули функции, если они есть, и построить на оси абсцисс соответствующие точки параболы.
Построить две какие-нибудь точки параболы, симметричные относительно ее оси. Для этого надо взять две точки на оси Ox, симметричные относительно точки  , и вычислить соответствующие значения функции (эти значения одинаковы). Например, можно построить точки параболы с абсциссами x=0 и x=2
, и вычислить соответствующие значения функции (эти значения одинаковы). Например, можно построить точки параболы с абсциссами x=0 и x=2 , если
, если  ≠0 (ординаты этих точек равны c).
≠0 (ординаты этих точек равны c).
Провести через построенные точки параболу. Заметим, что для более точного построения графика полезно найти еще несколько точек параболы.
Пример 1. Построим график функции y= -4x+3.
-4x+3.
Найдем координаты вершины параболы:
 =-
=-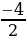 =2;
=2; 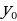 =
=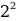 -7*2+10=-1.
-7*2+10=-1.
Построим точку (2;-1).

Проведем через точку (2;-1) прямую, параллельную оси ординат – ось симметрии параболы.

Решая уравнение  -4x+3=0, найдем нули функции:
-4x+3=0, найдем нули функции: 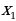 =1,
=1, 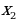 =3. Построим точки (1;0) и (3;0).
=3. Построим точки (1;0) и (3;0).

Возьмем две точки на оси Ox, симметричные относительно точки x=2, например, точки x=0 и x=4. Вычислим значение функции в этих точках: y(0)=y(4)=3. Построим точки (0;3) и (4;3)

Проведем параболу через построенные точки.

Итак, мы построили график квадратичной функции, не выделяя при этом полный квадрат.
Пример 2. Построить график функции y=3 -8x+4.
-8x+4.
Найдем координаты вершины параболы:
 =-
=-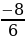 =1
=1 ;
; 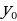 =3*
=3*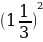 -8*1
-8*1 +4=-1
+4=-1 .
.
Построим точку (1 ;-1
;-1 ).
).
Проведем через точку (1 ;-1
;-1 ) прямую, параллельную оси ординат – ось симметрии параболы.
) прямую, параллельную оси ординат – ось симметрии параболы.
Решая уравнение 3 -8x+4=0, найдем нули функции:
-8x+4=0, найдем нули функции: 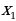 =2,
=2, 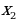 =
=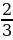 . Построим точки (2;0) и (
. Построим точки (2;0) и (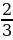 ;0).
;0).
Возьмем две точки на оси Ox, симметричные относительно точки x=1 , например, точки x=0 и x=2
, например, точки x=0 и x=2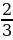 . Вычислим значение функции в этих точках: y(0)=y(2
. Вычислим значение функции в этих точках: y(0)=y(2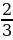 )=4. Построим точки (0;4) и (2
)=4. Построим точки (0;4) и (2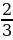 ;4)
;4)
Проведем параболу через построенные точки.
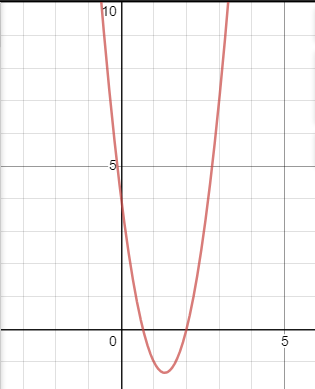
Пример 3. Построить график функции y=0,5 +3x+2,5.
+3x+2,5.
Найдем координаты вершины параболы:
 =-
=-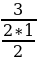 =-3;
=-3; 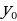 =3*
=3*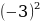 -8*(-3)+2,5=-2.
-8*(-3)+2,5=-2.
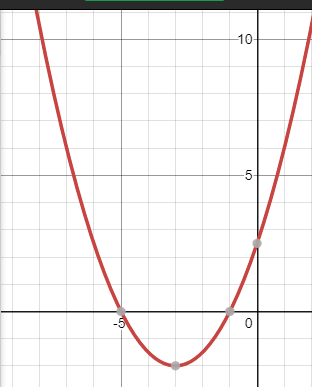
Построим точку (-3;-2).
Проведем через точку (-3;-2) прямую, параллельную оси ординат – ось симметрии параболы.
Решая уравнение 0,5 +3x+2,5=0, найдем нули функции:
+3x+2,5=0, найдем нули функции: 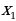 =-1,
=-1, 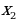 =-5. Построим точки (-1;0) и (-5;0).
=-5. Построим точки (-1;0) и (-5;0).
Возьмем две точки на оси Ox, симметричные относительно точки x=-3, например, точки x=0 и x=-6. Вычислим значение функции в этих точках: y(0)=y(-6)=2,5. Построим точки (0;2,5) и (-6;2,5)
Проведем параболу через построенные точки.
Пример 4. Построить график функции y=-2 +3x+2.
+3x+2.
Найдем координаты вершины параболы:
 =-
=-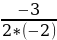 =
=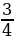 ;
; 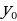 =-2*
=-2*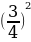 +3*
+3*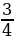 +2=3
+2=3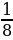 .
.
Построим точку (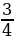 ;3
;3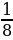 ).
).
Проведем через точку (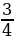 ;3
;3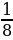 ) прямую, параллельную оси ординат – ось симметрии параболы.
) прямую, параллельную оси ординат – ось симметрии параболы.
Решая уравнение -2 +3x+2=0, найдем нули функции:
+3x+2=0, найдем нули функции: 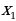 =2,
=2, 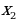 =-
=- . Построим точки (2;0) и (-
. Построим точки (2;0) и (- ;0).
;0).
Возьмем две точки на оси Ox, симметричные относительно точки x=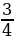 , например, точки x=0 и x=1
, например, точки x=0 и x=1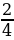 . Вычислим значение функции в этих точках: y(0)=y(1
. Вычислим значение функции в этих точках: y(0)=y(1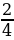 )=2. Построим точки (0;2) и (1
)=2. Построим точки (0;2) и (1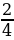 ;2)
;2)
Проведем параболу через построенные точки.

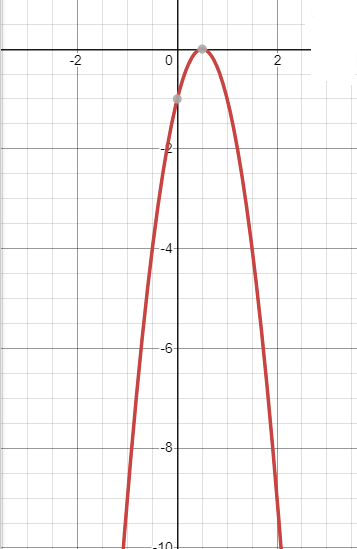
Пример 5. Построить график функции y=-4 +4x-1.
+4x-1.
Найдем координаты вершины параболы:
 =-
=-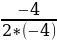 =
= ;
; 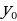 =-4*
=-4*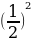 +4*
+4* -1=0.
-1=0.
Построим точку ( ;0).
;0).
Проведем через точку ( ;0) прямую, параллельную оси ординат – ось симметрии параболы.
;0) прямую, параллельную оси ординат – ось симметрии параболы.
Решая уравнение -4 +4x-1=0, найдем нули функции: x=0,5. В данном случае функция имеет только один нуль – точку (0,5; 0), которая является вершиной параболы.
+4x-1=0, найдем нули функции: x=0,5. В данном случае функция имеет только один нуль – точку (0,5; 0), которая является вершиной параболы.
Возьмем две точки на оси Ox, симметричные относительно точки x= , например, точки x=0 и x=1. Вычислим значение функции в этих точках: y(0)=y(1)=-1. Построим точки (0;-1) и (1;-1)
, например, точки x=0 и x=1. Вычислим значение функции в этих точках: y(0)=y(1)=-1. Построим точки (0;-1) и (1;-1)
Проведем построение дополнительных точек: x=-1 и x=3. Вычислим значение функции в этих точках: y(-1)=y(3)=-9. Построим точки (-1;-9) и (3; -9).
Проведем параболу через построенные точки.
Приведем примеры практических заданий, в которых используются свойства квадратичной функции.
Для начала вспомним свойства, которые нам понадобятся:
Функция y =ax2+bx+c принимает наименьшее или наибольшее значение в точке  =-
=-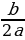 , которая является вершиной параболы.
, которая является вершиной параболы.
При этом, если a0, то функция имеет наименьшее значение, а если a, то функция имеет наибольшее значение.
Пр.з.1. Число 15 представить в виде суммы двух чисел так, чтобы произведение этих чисел было наибольшим.
Решение, Пусть x и (15-x) – данные числа. Тогда их произведение x(15-x) должно быть наибольшим.
Рассмотрим функцию y=x(15-x), y=- +15x – квадратичная функция, график – парабола.
+15x – квадратичная функция, график – парабола.
a=-1  =-
=-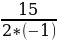 =
=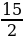 = 7,5
= 7,5
Итак, 7,5 – первое число, тогда 15-7,5 = 7,5 – второе число.
Ответ: Эти числа 7,5 и 7,5.
Пр.з.2. Сумма двух чисел равна 10. Найти эти числа, если сумма их кубов является наименьшей.
Решение. Пусть x и (10-x) – искомые числа. Тогда сумма их кубов:
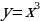 +
+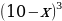 , у=
, у=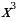 +(1000-3*100x+3*10
+(1000-3*100x+3*10 -
-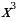 ), у=
), у=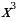 +1000-300x+30
+1000-300x+30 -
-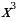 , у=30
, у=30 -300x+1000 – квадратичная функция, график – парабола.
-300x+1000 – квадратичная функция, график – парабола.
a=301, значит, ветви параболы направлены вверх, и наименьшее значение парабола принимает в ее вершине.
 =-
=-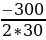 =5.
=5.
Итак, первое число – 5, тогда второе 10-5=5.
Ответ: Эти числа 5 и 5.
Номера из учебника: №624(1,2), 625(2,4).
Решение:
№624:
1) y= -7x+10.
-7x+10.

y0 при x5
yпри 2
y возрастает при x3,5
y убывает при x
a=10, значит функция принимает наименьшее значение в своей вершине, то есть при  =-
=-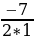 =3,5.
=3,5.
2) y=- +x+2.
+x+2.

y0 при -1
yпри x2
y возрастает при x
y убывает при x0,5
a=-1 =-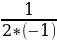 =0,5.
=0,5.
№625:
2) y=-3 -2x+1.
-2x+1.

yпри x
yпри -1
y возрастает при x
y убывает при x-
a=-3 =-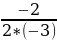 =-
=- .
.
4) y=3 -8x+4.
-8x+4.

yпри 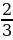
y0 при x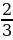 , x2
, x2
y возрастает при x1
y убывает при x
a=30, значит функция принимает наименьшее значение в своей вершине, то есть при  =-
=-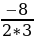 =1
=1 .
.







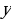 =
=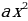 и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐.
и 𝑦 =𝑎𝑥2+𝑏𝑥+𝑐.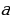 1 и её свойства
1 и её свойства 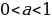 и её свойства
и её свойства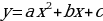 методом выделения полного квадрата
методом выделения полного квадрата

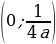 .
.

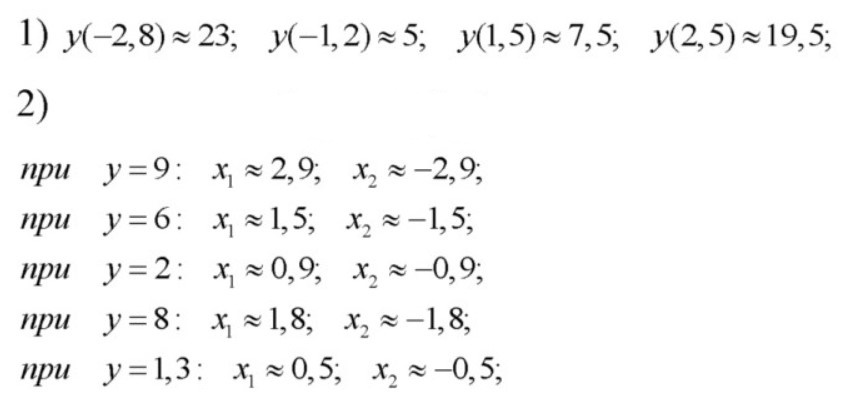

 x2 и сравним его с графиком функции y = x2.
x2 и сравним его с графиком функции y = x2. вдоль оси Oy к оси Ox в 2 раза.
вдоль оси Oy к оси Ox в 2 раза.

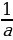 раз, следовательно, график функции y = ax2 получается из графика функции y = x2 сжатием его в
раз, следовательно, график функции y = ax2 получается из графика функции y = x2 сжатием его в 



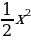 . По графику приближенно найти:
. По графику приближенно найти:
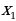 =-1,5,
=-1,5, 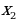 =1,5
=1,5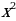

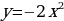 и сравним его с графиком функции y = 2x2.
и сравним его с графиком функции y = 2x2.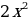 .
.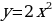
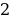
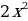
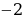

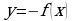 , надо построить график функции
, надо построить график функции 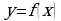 , а затем все точки этого графика отразить от оси
, а затем все точки этого графика отразить от оси 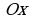 .
.


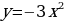 . По графику приближенно найти:
. По графику приближенно найти:
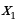 ≈ 1,7;
≈ 1,7; 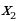 ≈ -1,7
≈ -1,7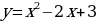

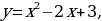 используя метод выделения полного квадрата:
используя метод выделения полного квадрата: 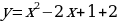 ,
, 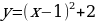 .
.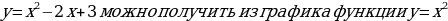 следующими преобразованиями:
следующими преобразованиями: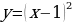 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 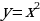 вправо на 1 единицу.
вправо на 1 единицу.
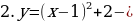 сдвиг (параллельный перенос)
сдвиг (параллельный перенос) 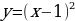 вверх на 2 единицы.
вверх на 2 единицы.
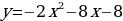 из графика функции
из графика функции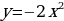 с помощью выделения полного квадрата.
с помощью выделения полного квадрата.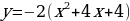 ,
, 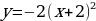 .
.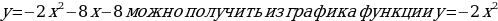 следующим преобразованием:
следующим преобразованием:
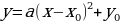 является парабола, получаемая сдвигом параболы
является парабола, получаемая сдвигом параболы 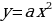 :
: , если
, если 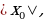 если
если 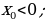
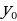 , если
, если 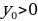 ;
;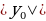 , если
, если 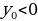 .
.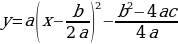 , т.е. в виде
, т.е. в виде 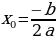 и
и 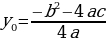 .
.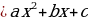 можно также назвать параболой.
можно также назвать параболой. 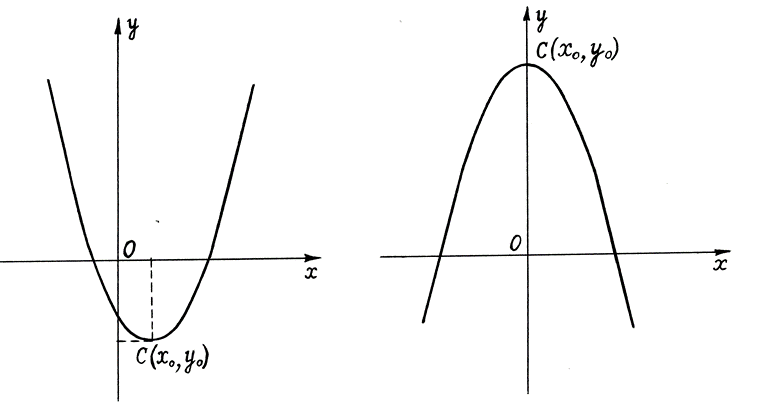
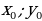 ) вершины параболы
) вершины параболы 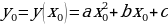 .
.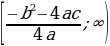 , если а0
, если а0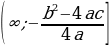 , если а
, если а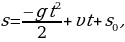 где
где 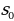 – расстояние от тела до поверхности земли в момент времени t=0.
– расстояние от тела до поверхности земли в момент времени t=0. Выразите площадь прямоугольника.
Выразите площадь прямоугольника.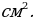
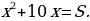
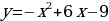
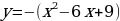
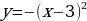
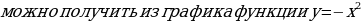 следующими преобразованием:
следующими преобразованием: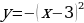 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 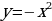 вправо на 3 единицы.
вправо на 3 единицы.
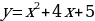
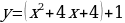 ,
, 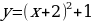 .
. следующим преобразованиями:
следующим преобразованиями: сдвиг (параллельный перенос) графика функции
сдвиг (параллельный перенос) графика функции  сдвиг (параллельный перенос) графика функции
сдвиг (параллельный перенос) графика функции  вверх на 1 единицы
вверх на 1 единицы
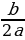
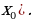
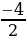 =2;
=2; 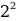 -7*2+10=-1.
-7*2+10=-1.




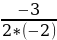 =
=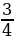 ;
; 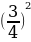 +3*
+3*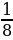 .
.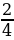 . Вычислим значение функции в этих точках: y(0)=y(1
. Вычислим значение функции в этих точках: y(0)=y(1
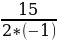 =
=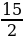 = 7,5
= 7,5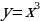 +
+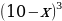 , у=
, у=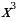 +(1000-3*100x+3*10
+(1000-3*100x+3*10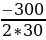 =5.
=5.
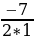 =3,5.
=3,5.
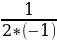 =0,5.
=0,5.

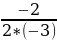 =-
=-
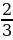
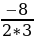 =1
=1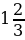 x2 и сравним его с графиком функции y = x2.
x2 и сравним его с графиком функции y = x2.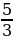 x2
x2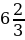

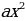 при
при 
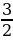 раза. Графически это означает, что график функции y =
раза. Графически это означает, что график функции y = 

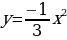 и сравним его с графиком функции y =
и сравним его с графиком функции y = 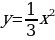 .
.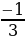
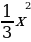 от оси Ox
от оси Ox
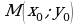 , принадлежащей графику функции
, принадлежащей графику функции 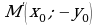 , принадлежащая графику функции
, принадлежащая графику функции 


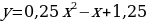 из графика функции
из графика функции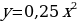 с помощью выделения полного квадрата.
с помощью выделения полного квадрата.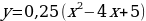 ,
, 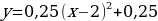 .
.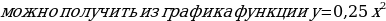 следующими преобразованиями:
следующими преобразованиями: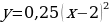 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 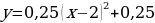 - сдвиг (параллельный перенос)
- сдвиг (параллельный перенос) 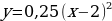 вверх на 0,25 единиц.
вверх на 0,25 единиц.
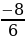 =1
=1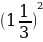 -8*1
-8*1
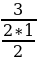 =-3;
=-3; 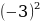 -8*(-3)+2,5=-2.
-8*(-3)+2,5=-2.
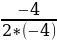 =
= +4*
+4*










