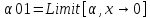инновационные ТЕХНОЛОГИИ В МАТЕМАТИКЕ
Гребенникова Елена Александровна,
Новосибирский государственный педагогический институт
E-mail: [email protected]
Аннотация. Исследуется и доказывается возможность применения новых технологий в изучении математики. Приведены примеры использования специализированных математических пакетов. Ключевые слова: информационные технологии, специализированные математические пакеты, пакет Wolfram Mathematicaция, функции, обучение.
Давно замечено, что из всех наук наиболее быстро развиваются точные. В настоящее время происходит интенсивная математизация знания, предполагающая, во-первых, обобщение уже достигнутого той или иной наукой и выделение нескольких ее основных утверждений (аксиом); во-вторых, закрепление принципов вывода, согласно которым утверждение данной науки логически вытекало из аксиом.
С другой стороны, растет множество специалистов-нематематиков, которым математика в настоящее время нужна в гораздо большем объеме, чем она излагалась в школе. Это– те специалисты, которые пытаются использовать математические методы в своих исследованиях [1]. Однако на практике очевидно либо наличие нечетких математических понятий, либо их отсутствие. Овладение же способом математического видения и описания объектов реального мира, на наш взгляд, должно стать обязательным атрибутом высококвалифицированного специалиста XXI века.
Математические формулы – лишь удобный язык для изложения идей и методов математики. Сами же эти идеи можно описать, используя привычные и наглядные образы из окружающей жизни. Математические понятия – понятия отвлеченные, абстрактные. Это лишь слепок с реального мира, его бледный силуэт. Выделяя абстрактные понятия в чистом виде, отсекая второстепенные детали, математик всегда обедняет жизнь.
Математическая мысль не исчерпывает всех проявлений человеческого разума. Однако еще Чарльз Дарвин утверждал, что у людей, усвоивших великие принципы математики, одним органом чувств больше, чем у простых смертных.
Одним из основных понятий математики является понятие функции. Покажем, как можно сформировать или уточнить это понятие (алгоритм приведен в [3]). Обратимся к задачам. Обсудим вопрос: нам необходимо повесить картину. Математическое обоснование следует сделать такое: в основу вывода положены две строгие математические зависимости. Первая устанавливает соответствие между следующими величинами: расстояние от нас до картины. Вторая связывает размеры картины и ее расположение на стене относительно пола. Такое соответствие принято называть в математике функцией одного аргумента.
Современная математика знает множество функций, и у каждой неповторимый облик, который можно представить сложенным из набора характерных деталей, в которых проявляются основные свойства функций. Функции – это математические портреты устойчивых закономерностей, познаваемых человеком.
Задача. На стене висит картина.
Высота картины 1,4м и располагается на 1,8м выше уровня глаз человека. На каком расстоянии от стены нужно встать, чтобы угол обзора был наибольшим?
![]()

1,4

![]()



 1,8
1,8
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
х
Решение.
Составляем функцию  (х), где
(х), где  – это угол обзора, а х – расстояние до стены.
– это угол обзора, а х – расстояние до стены.
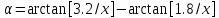
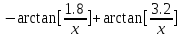
Находим производную функции  `(x).
`(x).
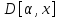

Производную приравниваем к нулю.
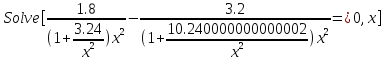
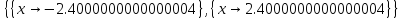
Найдем  (2,4). Найдем значение угла в радианах.
(2,4). Найдем значение угла в радианах.


Найдем значение угла в градусах.
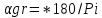
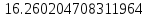
Найдем предел функции  (х) при х-0, х-
(х) при х-0, х- .
.
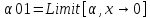


Предел получился равным нулю.
Находим максимальное значение среди стационарных точек.

Строим график функции  (х).
(х).

Изобразить графически приведенные зависимости средствами языков программирования высокого уровня (TBasic, TPascal и др.) без соответствующей подготовки практически невозможно. Приведенные трудности можно успешно преодолеть, если использовать возможности специальных математических пакетов. Таким пакетом может быть хорошо зарекомендовавший себя пакет пакет Wolfram Mathematicaовна:
Задача 1. На стене весит картина, высота картины равна 1,4 метра, и картина располагается на 1,8 м выше уровня глаз человека. На каком расстоянии от стены нужно встать, чтобы угол обзора был наибольшим.
Решение:
Составляем функцию  , где х – расстояние от месторасположение человека до стены.
, где х – расстояние от месторасположение человека до стены.






1,4


1,8
![]()
х
2. Находим значение производной функции 
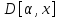

3. Решаем уравнение  =0
=0
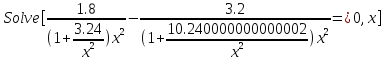
Получаем стационарные точки, по условию задачи удовлетворяет положительная точка
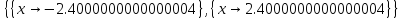
4. Определяем значение функции в полученной точке (значение вычисляется в радианах):


5. Полученное значение переводим в градусы
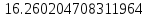
6. Вычисляем значение пределов на концах отрезка:



7. Вычисляем наибольшее значение между полученными результатами

8. Изображаем полученный результат в виде графика на промежутке [0,10]
На графике видно, что наибольшее значение достигается именно в точке 2,4
Задача 2. На стене весит картина, высота картины равна 1,4 метра, человек располагается на расстоянии 5 метров. На каком расстоянии от уровня глаз необходимо повесить картину, чтобы угол обзора был наибольшим.
Решение:
Составляем функцию  , где х – расстояние от уровня глаз человека до картины.
, где х – расстояние от уровня глаз человека до картины.

Задача: При каком значении h, x угол обзора будет наибольшим
Составляем функцию  , где h – расстояние от уровня глаз человека до картины, х – расстояние от человека до стены.
, где h – расстояние от уровня глаз человека до картины, х – расстояние от человека до стены.

Находим значение частных производных функции  )
)

Решаем систему уравнений, приравнивая частные производные к нулю:
Система решения не имеет

Находим наибольшее значение на концах промежутка:
Изображаем графически:
-
-
 Задача 2: Коридоры поворачиваются под прямым углов, до поворота ширина b м, ширина после поворота a м. Какова максимальная длина трубы, которую можно горизонтально пронести через коридор?
Задача 2: Коридоры поворачиваются под прямым углов, до поворота ширина b м, ширина после поворота a м. Какова максимальная длина трубы, которую можно горизонтально пронести через коридор?




 а (м)
а (м)
 а
а
b (м)

Решение:
Рассматриваем пучок прямых y=k*x. Определяем координаты точек A и B, при котором длина отрезка AB, получающегося при пересечении длины с коридором, будет минимальной. Задаем функцию Fk:
В программе получаем:

Находим производную полученной функции:

В программе получаем:
Решаем уравнение, приравняв производную к нулю
Программой получили точки, одну положительную, три отрицательных). Будем рассматривать положительную точку.
Определяем значение функции Fk в полученной точке (k):
Программой получаем результат:

Вычисляем значение пределов на концах, при условии a=3(м), b=4(м)


Получим значение в конкретных точках:
Программа выдаст результат: 
50 Попробуем упростить полученное выражение:

Если хотим в десятичных дробях получить ответ, тогда:

Программа выдаст результат: 
Вычисляем значение пределов: (при  )
)

Программа выдает: 
Вычисляем значение пределов: (при  )
)

Программа выдает: 
Минимальное значение получаем в экстремальной точке ( )
)
Находим длину, вычисляя корень квадратный
Программа выдает: 


 Задача: Начальные условия с предыдущей задачи, но угол перегиба коридоров происходит под величиной 45
Задача: Начальные условия с предыдущей задачи, но угол перегиба коридоров происходит под величиной 45

 y a (м) B
y a (м) B



 45
45


 x
x
![]() b (м)
b (м)
A
Решение:
l1+l2=a/( sin
sin )+a/sin(45-
)+a/sin(45- )
)
Для начальных условий возьмем а=2
1. Введем функцию, зависимую от  :
:
Программа выдаст результат:
2. Найдем производную функции: 
Программа выдаст результат:
3. Приравниваем производную к нулю, вводя ограничения на  ,
,  =0.01,
=0.01, 
После выполнения программа выдаст результат:
4. Находим значение функции в полученной точке
Программа выдаст результат:

Получаем, что при а=2, максимальная длина пронесенного предмета составляет  8,86(м)
8,86(м)
литература.
1. Жмурова И. Ю., Генералова А. А. Оптимизационные задачи в школьном курсе математики // Молодой ученый. — 2016. — №14. — С. 537-539.
https://moluch.ru/archive/118/32649/
Может быть полезна при подготовке вашей первой статьи. Обосновывается, почему полезно в школе рассматривать оптимизационные задачи.
2.Прикладные задачи на экстремумы, Куликова О.А. http://nsportal.ru/shkola/algebra/library/2011/10/19/prikladnye-zadachi-na-ekstremumy












 1,8
1,8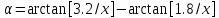
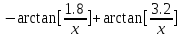
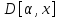

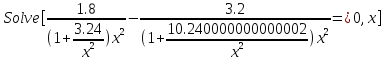
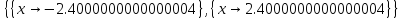


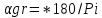
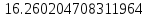
 .
.