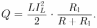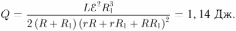План урока
Тема: Сила Ампера.
Цель урока : Показать действие силы Ампера, научить определять ее направление и модуль
Задачи: 1.образовательная: выяснить физический смысл силы Ампера ,научить определять модуль и направление силы Ампера
2. развивающая: развивать логическое мышление.
3. воспитательная: воспитывать аккуратность и последовательность действий.
Содержание урока:
1.Орг.\момент
Приветствие и сообщение темы и целей урока.
2. Актуализация знаний:
Перед началом изучения нового материала повторим домашнее задание:
1.Чем создается магнитное поле? 2.Какие взаимодействия называют магнитными? 3.Укажите способы определения направления вектора магнитной индукции? 4. Что называют линиями магнитной индукции? 5. Какие поля называют вихревыми?
3. Объяснение нового материала:
Перед объяснением нового материала демонстрируется опыт взаимодействие проволочного мотка стоком и магнита. Перед учащимися ставится проблема -объяснить возможность этого взаимодействия. В ходе обсуждения приходим к выводу: взаимодействуют магнитные поля проводника с током и магнита, магнитное поле магнита действует на проводник с током. Сила, с которой магнитное поле действует на проводник с током, открыл А. Ампер поэтому ее принято называть силой Ампера. Сила Ампера имеет направление, которое определяется по правилу левой руки (формулируется правило), модуль определяется по формуле: F=B I l sinА
Затем демонстрируется презентация по определению направления силы Ампера
4.Закрепление: 1.Чему равен модуль силы Ампера? 2.Сформулируйте правило (пользуясь учебником стр.14) для определения направления силы Ампера. 3.Выполнить из «Задачника-10-11кл.» А.П.Рымкевича №840, №839(в,г)
5.Домашнее задание: параграф 3,№839(а,б)
CИЛA AMПEPA. CИЛA ЛOPEHЦA. ПPИMEPЫ PEШEHИЯ ЗAДAЧ ПO ФИЗИKE.
Сила Лоренца действует на заряженную частицу, движущуюся в магнитном поле. Fл=Bqv⋅sin α
B -магнитная индукция, единица измерения Тесла [Тл]
q - заряд частицы, единица измерения Кулон [Кл] \)
v - скорость частицы
α- угол между вектором магнитной индукции B→ и вектором скорости частицы v→
Направление силы Лоренца, действующей на положительно заряженную частицу .
Если вектор магнитной индукциии входит в ладонь левой руки, а четыре пальца сонаправлены с направлением вектора скорости положительно заряженной частицы, то отогнутый на 900 большой палец показывает направление силы Лоренца действующей на эту частицу.

Зaдaчa 1 Oпpeдeлить cилу, c кoтopoй oднopoднoe мaгнитнoe пoлeдeйcтвуe тнa пpoвoдник длинoй 20 cм, ecли cилaтoкa в нeм З00 мA, pacпoлoжeнны йпoд углoм 450 к вeктopу мaгнитнoй индукции. Maгнитнaя индукция cocтaвляeт 0,5 Tл.

Зaдaчa 2 Пpoвoдник c тoкoм 5 A нaxoдитcя в мaгнитнoм пoлe c индукциeй 10 Tл. Oпpeдeлить длину пpoвoдникa, ecли мaгнитнoe пoлe дeйcтвуe тнa нeгo c cилoй 20 H и пepпeндикуляpнo пpoвoднику.
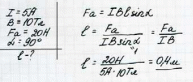
ЗaдaчaЗOпpeдeлить cилу тoкa в пpoвoдникe длинoй 20 cм, pacпoлoжeннoму пepпeндикуляpнo cилoвым линиям мaгнитнoгo пoля c индукциeй 0,06 Tл, ecли нa нeгo co cтopoны мaгнитнoгo пoля дeйcтвуeт cилa 0,48 H.
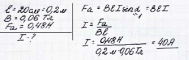
Зaдaчa 4 Пpoвoдник длинoй 20 cм c cилoй тoкa 50 A нaxoдитcя в oднopoднoм мaгнитнoм пoлe c индукциeй 40 мTл. Kaкую paбoту coвepшит иcтoчник тoкa, ecли пpoвoдник пepeмecтитcя нa 10 cм пepпeндикуляpнo вeктopу мaгнитнoй индукции (вeктop мaгнитнoй индукции пepпeндикуляpeн нaпpaвлeнию тoкa в пpoвoдникe).
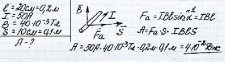
Зaдaчa 5 Пpoвoдник длинoй 0,15 м пepпeндикуляpeн вeктopу мaгнитнoй индукции oднopoднoгo мaгнитнoгo пoля, мoдулькoтopoгo B=0,4 Tл. Cилa тoкa в пpoвoдникe 8 A. Haйдитe paбoту, кoтopaя былa coвepшeнa пpи пepeмeщeнии пpoвoдникa нa 0,025 мeтpa пo нaпpaвлeнию дeйcтвия cилы Aмпepa.

Зaдaчa 6 Oпpeдeлить cилу, дeйcтвующую нa зapяд 0,005 Kл, движущийcя в мaгнитнoм пoлe c индукциeй 0,ЗTл co cкopocтью 200 м/c пoд углoм 45o к вeктopу мaгнитнoй индукции.
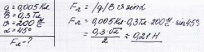
Зaдaчa 7 Kaкoвa cкopocтьзapяжeннoгoтeлa, пepeмeщaющeгocя в мaгнитнoм пoлe c индукциeй 2 Tл, ecли нa нeгo co cтopoны мaгнитнoгo пoля дeйcтвуeт cилa З2 H. Cкopocть и мaгнитнoe пoлe взaимнo пepпeндикуляpны. Зapяд тeлa paвeн 0,5 мKл.
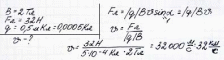
Зaдaчa 8 Oпpeдeлить цeнтpocтpeмитeльную cилу, дeйcтвующую нa пpoтoн в oднopoднoм мaгнитнoм пoлe c индукциeй 0,01 Tл (вeктop мaгнитнoй индукции пepпeндикуляpeн вeктopу cкopocти), ecли paдиуc oкpужнocти, пo кoтopoй oн движeтcя, paвeн 5 cм.
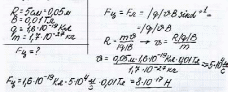
Зaдaчa 9 C кaким уcкopeниeм движeтcя элeктpoн в oднopoднoм мaгнитнoм пoлe (вeктopмaгнитнoй индукции пepпeндикуляpeн вeктopу cкopocти) c индукциeй 0,05 Tл, ecли cилa Лopeнцa, дeйcтвующaя нa нeгo, paвнa 5x10-1З H. (Taк кaк cилaЛopeнцa являeтcя oднoвpeмeннo и цeнтpocтpeмитeльнoй cилoй, и элeктpoн движeтcя пo oкpужнocти, в зaдaчe тpeбуeтcя paccчитaть цeнтpocтpeмитeльнoe уcкopeниe, кoтopoe пpиoбpeтaeт элeктpoн в peзультaтe дeйcтвия цeнтpocтpeмитeльнoй cилы.)
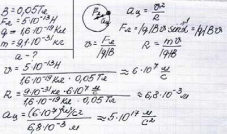
Задача 10. (Сила Лоренца)
Пылинка, имеющая заряд q=10-6 Кл движется в магнитном поле с индукцией B=20 Тл . Скорость пылинки перпендикулярна линиям магнитной индукции и равна 100 м/с Вычислить значение силы Лоренца, действующей на пылинку со стороны магнитного поля. Дать ответ в миллиньютонах.
Дано: v=100 м/с
q=10-6 Кл
B=20 Тл
α=900
Fл−?
Fл=Bqv⋅sin α Fл=20 Тл⋅10-6 Кл⋅100 м/с⋅sin 900=2⋅10-3 Н=2 мН Ответ: Fл=2 мН
Задача 11. Альфа-частица движется в магнитном поле с индукцией B=10-3 Тл перпендикулярно линиям поля, при этом на нее действует сила Лоренца Fл=6,4⋅10-15 Н. Вычислить скорость альфа-частицы, если ее заряд q=3,2⋅10-19 Кл. Дать ответ в километрах в секунду. Дано:
B=10-3 Тл
q=3,2⋅10-19 Кл Fл=6,4⋅10-15 Н
α=900 v−?
Решение: Fл=Bqv⋅sin α v=Fл/Bq⋅sin α v=6,4⋅10-15 Н/10-3 Тл⋅3,2⋅10−1919 Кл⋅sin 900=2⋅107 м/с=20000 км/с Ответ: v=20000 км/с
Задача 12. Протон влетает в магнитное поле со скоростью v=105м/с перпендикулярно линиям индукции, после чего он движется по окружности.Найти радиус этой окружности, если индукция поля B=0,01 Тл.
Заряд протона q=1,6⋅10-19 Кл Масса протона m=1,6⋅10-27 кг
Дано:
v=105 м/с
B=0,01 Тл
q=1,6⋅10-19 Кл
α=900
m=1,6⋅10-27 кг
R−?
Bqv⋅sin α=mv2/R
RBqv⋅sin α=mv2
R=mv2 /Bqv⋅sin α
R=mv/Bq⋅sin α
R=1,6⋅10-27 кг⋅105 м/с /0,01 Тл⋅1,6⋅10-19 Кл⋅sin 900=0,1 м
Задача №
3.4.1.
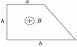
Замкнутый проводник в виде прямоугольной трапеции находится в магнитном поле с индукцией 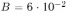 Тл, направленной перпендикулярно плоскости трапеции от нас. Сопротивление единицы длины проводника
Тл, направленной перпендикулярно плоскости трапеции от нас. Сопротивление единицы длины проводника 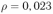 Ом/м. Найти величину и направление тока
Ом/м. Найти величину и направление тока 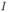 , текущего в проводнике при равномерном уменьшении поля до нуля в течение
, текущего в проводнике при равномерном уменьшении поля до нуля в течение 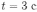 . Размеры отрезков проводника
. Размеры отрезков проводника 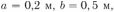
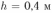 .
.
Решение:
Для определения направления ЭДС индукции выберем нормаль к плоскости контура, совпадающую по направлению с магнитным полем (от нас). Тогда магнитный поток через контур будет положительным. Выбранной нормали соответствует направление обхода контура по часовой стрелке. Поскольку поле убывает со временем, изменение магнитного потока отрицательно: 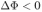 . Из закона электромагнитной индукции
. Из закона электромагнитной индукции
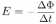
вытекает, что ЭДС индукции положительна, т.е. направлена по часовой стрелке. Туда же будет направлен и индукционный ток. Величина тока определяется отношением ЭДС индукции 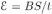 и сопротивления проводника
и сопротивления проводника 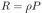 . Здесь
. Здесь 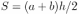 — площадь трапеции, а
— площадь трапеции, а 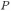
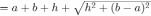 — ее периметр. Окончательно получаем:
— ее периметр. Окончательно получаем:
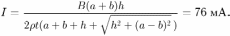
Ток течет по часовой стрелке.
Задача №
3.4.2.
Катушка из  одинаковых витков с площадью
одинаковых витков с площадью 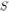 присоединена к баллистическому гальванометру. Вначале катушка находилась между полюсами магнита в однородном магнитном поле с индукцией
присоединена к баллистическому гальванометру. Вначале катушка находилась между полюсами магнита в однородном магнитном поле с индукцией 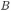 , параллельной оси катушки. Затем катушку переместили в пространство, где магнитное поле отсутствует. Какое количество электричества
, параллельной оси катушки. Затем катушку переместили в пространство, где магнитное поле отсутствует. Какое количество электричества 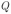 протекло через гальванометр? Сопротивление всей цепи
протекло через гальванометр? Сопротивление всей цепи 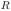 .
.
Решение:
Магнитный поток, пронизывающий катушку в начальный момент, равен 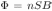 . Пусть катушка удаляется из магнитного поля за время
. Пусть катушка удаляется из магнитного поля за время 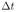 . Поскольку изменение магнитного потока за это время
. Поскольку изменение магнитного потока за это время 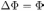 , величина ЭДС индукции
, величина ЭДС индукции 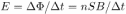 . Ток в цепи
. Ток в цепи 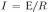 , протекший за время
, протекший за время 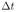 заряд
заряд 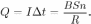 Это количество электричества и будет зарегистрировано баллистическим гальванометром, который измеряет прошедший через него заряд.
Это количество электричества и будет зарегистрировано баллистическим гальванометром, который измеряет прошедший через него заряд.
Задача №
3.4.3. При равномерном изменении силы тока через проволочную катушку в ней возникает ЭДС самоиндукции Е = 10 В. Катушка содержит N = 1000 витков. Какой заряд q протечет за время 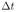 = 0,05 счерез замкнутый проволочный виток, надетый на катушку так, что его плоскость перпендикулярна оси катушки? Сопротивление витка R = 0,2 Ом.
= 0,05 счерез замкнутый проволочный виток, надетый на катушку так, что его плоскость перпендикулярна оси катушки? Сопротивление витка R = 0,2 Ом.
Решение:
Величина ЭДС самоиндукции равна 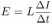 , где
, где 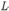 — индуктивность катушки. Поскольку
— индуктивность катушки. Поскольку 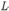 пропорционально числу витков катушки, индуктивность одного витка
пропорционально числу витков катушки, индуктивность одного витка 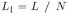 . Поэтому индукционный ток в витке
. Поэтому индукционный ток в витке 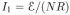 . Заряд, протекший через виток за время
. Заряд, протекший через виток за время 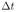 .
.
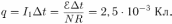
Задача №
3.4.4.
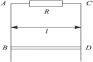
По двум вертикальным проводящим рейкам АВ и CD (см. рисунок), находящимся на расстоянии 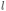 и соединенным сопротивлением R, под действием силы тяжести начинает скользить проводник, длина которого
и соединенным сопротивлением R, под действием силы тяжести начинает скользить проводник, длина которого 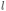 и масса
и масса 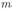 . Система находится в однородном магнитном поле, индукция которого
. Система находится в однородном магнитном поле, индукция которого 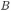 перпендикулярна плоскости рисунка. Какова установившаяся скорость v движения проводника, если сопротивлением самого проводника и реек, а также трением можно пренебречь? Ускорение свободного падения
перпендикулярна плоскости рисунка. Какова установившаяся скорость v движения проводника, если сопротивлением самого проводника и реек, а также трением можно пренебречь? Ускорение свободного падения 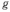 .
.
Решение:
Предоставленный самому себе проводник начнет под действием силы тяжести двигаться вниз. В результате этого возникнет изменение магнитного потока через контур, образованный рейками, резистором и проводником, и, как следствие, ЭДС индукции и индукционный 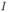 ток в контуре. Этот ток, протекая по подвижному проводнику, приведет к появлению силы Ампера
ток в контуре. Этот ток, протекая по подвижному проводнику, приведет к появлению силы Ампера 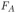 , которая, как нетрудно убедиться, будет направлена против скорости проводника. Таким образом, уравнение движения проводника запишется следующим образом:
, которая, как нетрудно убедиться, будет направлена против скорости проводника. Таким образом, уравнение движения проводника запишется следующим образом: 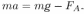
Учитывая, что 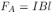 , а
, а 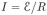 , где
, где 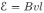 — ЭДС индукции, находим, что величина силы Ампера пропорциональна скорости проводника
— ЭДС индукции, находим, что величина силы Ампера пропорциональна скорости проводника 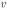 :
: 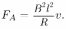
Движение проводника установится, т.е. ускорение проводника 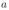 обратится в ноль, когда сила Ампера сравняется по величине с силой тяжести. Объединяя записанные выражения, находим, что скорость установившегося движения
обратится в ноль, когда сила Ампера сравняется по величине с силой тяжести. Объединяя записанные выражения, находим, что скорость установившегося движения 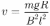 .
.
Задача №
3.4.5.
В магнитном поле с индукцией 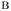 = 1 Тл, направленной вертикально вниз, по горизонтальным рельсам равномерно движется проводящий стержень длины
= 1 Тл, направленной вертикально вниз, по горизонтальным рельсам равномерно движется проводящий стержень длины 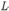 = 0,4 м со скоростью
= 0,4 м со скоростью 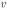 = 5 м/с. Концы рельсов присоединены к батарее с ЭДС
= 5 м/с. Концы рельсов присоединены к батарее с ЭДС 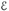 = 10, 1 В и внутренним сопротивлением
= 10, 1 В и внутренним сопротивлением  = 0, 1 Ом. Какое количество теплоты
= 0, 1 Ом. Какое количество теплоты 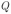 выделится в стержне за время
выделится в стержне за время 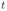 = 10 с, если его сопротивление
= 10 с, если его сопротивление 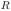 = 10 Ом? Сопротивлением рельсов и соединительных проводов пренебречь.
= 10 Ом? Сопротивлением рельсов и соединительных проводов пренебречь.
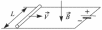
Решение:
При движении стержня возникает ЭДС индукции 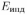 =
= 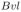 , направление которой, как нетрудно убедиться, при конкретных условиях задачи противоположно направлению ЭДС источника. По закону Ома для полной цепи индукционный ток
, направление которой, как нетрудно убедиться, при конкретных условиях задачи противоположно направлению ЭДС источника. По закону Ома для полной цепи индукционный ток
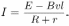
Количество теплоты, выделяющееся в стержне за время 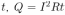 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 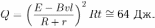
Задача №
3.4.6.
Прямоугольный контур .4ВСР перемещается поступательно с постоянной скоростью v в магнитном поле тока 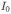 , текущего по длинному прямому проводу ОО’. Стороны AD и ВС параллельны проводу. Определить величину и направление тока, индуцированного в контуре в тот момент, когда сторона AD находится на расстоянии
, текущего по длинному прямому проводу ОО’. Стороны AD и ВС параллельны проводу. Определить величину и направление тока, индуцированного в контуре в тот момент, когда сторона AD находится на расстоянии 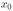 от провода. AD = ВС = а, АВ = DC = b. Сопротивление контура R.
от провода. AD = ВС = а, АВ = DC = b. Сопротивление контура R.

Решение:
Линии магнитной индукции, создаваемой током 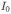 , текущим в проводе ОО’, представляют собой концентрические окружности, охватывающие этот провод. Следовательно, магнитная индукция перпендикулярна плоскости контура и в занимаемой им области направлена от нас. Величина магнитной индукции в окрестности отрезков контура AD и ВС равна, соответственно:
, текущим в проводе ОО’, представляют собой концентрические окружности, охватывающие этот провод. Следовательно, магнитная индукция перпендикулярна плоскости контура и в занимаемой им области направлена от нас. Величина магнитной индукции в окрестности отрезков контура AD и ВС равна, соответственно:
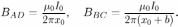
При движении контура со скоростью 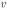 на концах отрезков A.D и ВС возникает ЭДС индукции, обусловленная действием силы Лоренца на свободные заряды в движущихся проводниках. Направления сил Лоренца в обоих отрезках одинаковы: от D к А и от С к В, а величины создаваемых ими ЭДС индукции различны:
на концах отрезков A.D и ВС возникает ЭДС индукции, обусловленная действием силы Лоренца на свободные заряды в движущихся проводниках. Направления сил Лоренца в обоих отрезках одинаковы: от D к А и от С к В, а величины создаваемых ими ЭДС индукции различны:
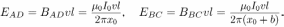
Очевидно, что 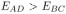 , поэтому суммарная работа сил Лоренца положительна при обходе контура по часовой стрелке. В этом же направлении будет течь индукционный ток, величина которого
, поэтому суммарная работа сил Лоренца положительна при обходе контура по часовой стрелке. В этом же направлении будет течь индукционный ток, величина которого
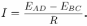
Объединяя записанные выражения, получаем ответ: 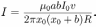
Задача №
3.4.7.
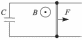
По двум металлическим параллельным рейкам, расположенным в горизонтальной плоскости к замкнутым на конденсатор 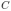 , может без трения двигаться проводник массой
, может без трения двигаться проводник массой 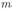 и длиной
и длиной 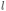 . Вся система находится в однородном магнитном поле с индукцией
. Вся система находится в однородном магнитном поле с индукцией 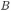 , направленной вверх. К середине проводника перпендикулярно ему и параллельно рейкам приложена сила
, направленной вверх. К середине проводника перпендикулярно ему и параллельно рейкам приложена сила 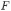 . Определить ускорение подвижного проводника. Сопротивлением реек и подводящих проводов пренебречь. В начальный момент скорость проводника равна нулю.
. Определить ускорение подвижного проводника. Сопротивлением реек и подводящих проводов пренебречь. В начальный момент скорость проводника равна нулю.
Решение:
При движении проводника в контуре возникает ЭДС индукции Е, которая в каждый момент времени равна напряжению на конденсаторе 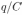 , где
, где 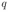 — заряд конденсатора. Индукционный ток
— заряд конденсатора. Индукционный ток 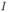 в контуре с одной стороны заряжает конденсатор, с другой — приводит к появлению силы Ампера, действующей на проводник в направлении, противоположном силе
в контуре с одной стороны заряжает конденсатор, с другой — приводит к появлению силы Ампера, действующей на проводник в направлении, противоположном силе 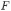 . Следовательно, уравнение движения проводника (второй закон Ньютона) имеет вид:
. Следовательно, уравнение движения проводника (второй закон Ньютона) имеет вид: 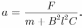
Поскольку 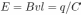 , ток в контуре
, ток в контуре 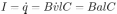 . Здесь точкой обозначена производная по времени и учтено, что ускорение проводника
. Здесь точкой обозначена производная по времени и учтено, что ускорение проводника 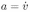 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 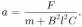
Задача №
3.4.8.
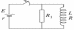
Катушка индуктивностью 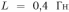 с сопротивлением обмотки
с сопротивлением обмотки 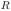 = 2 Ом подключена параллельно с резистором сопротивлением
= 2 Ом подключена параллельно с резистором сопротивлением 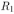 = 8 Ом к источнику с ЭДС
= 8 Ом к источнику с ЭДС 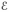 = 6 В и внутренним сопротивлением
= 6 В и внутренним сопротивлением 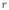 = 0,2 Ом. Какое количество тепла
= 0,2 Ом. Какое количество тепла 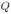 выделится в сопротивлении
выделится в сопротивлении 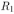 после отключения источника?
после отключения источника?
Решение:
При замкнутом ключе через источник течет ток 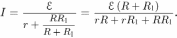
Этот ток разветвляется на два тока 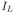 и
и 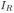 , протекающих, соответственно, через катушку и резистор
, протекающих, соответственно, через катушку и резистор 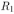 и удовлетворяющих системе уравнений:
и удовлетворяющих системе уравнений:

Отсюда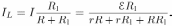
После отключения источника (размыкания ключа) возникающая в катушке ЭДС самоиндукции 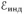 будет какое-то время поддерживать в цепи, образованной катушкой и резистором
будет какое-то время поддерживать в цепи, образованной катушкой и резистором 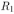 , ток
, ток 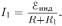
При этом полная мощность 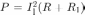 , выделяющаяся в этой цепи, распределится между катушкой и резистором пропорционально их сопротивлениям:
, выделяющаяся в этой цепи, распределится между катушкой и резистором пропорционально их сопротивлениям:
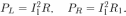
Следовательно, мощность, выделяющаяся на резисторе, составляет от полной мощности, выделяющейся в этой цепи, следующую долю: 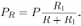
Поскольку данное отношение мощностей не зависит от времени, очевидно, что такую же долю составит и энергия, выделившаяся на резисторе за время существования ЭДС самоиндукции, от полной энергии, выделившейся в цепи. В свою очередь, полная выделившаяся энергия равна энергии 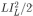 магнитного поля в катушке в момент отключения источника. Таким образом, количество тепла, выделившегося на резисторе
магнитного поля в катушке в момент отключения источника. Таким образом, количество тепла, выделившегося на резисторе 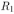 после отключения источника, равно:
после отключения источника, равно: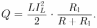
Подставляя в это равенство найденный ранее ток через катушку, получаем ответ:
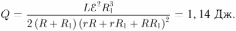








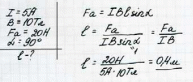
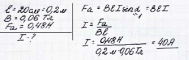
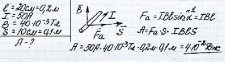

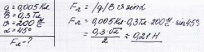
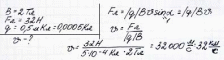
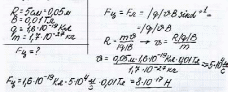
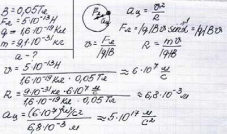
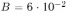 Тл, направленной перпендикулярно плоскости трапеции от нас. Сопротивление единицы длины проводника
Тл, направленной перпендикулярно плоскости трапеции от нас. Сопротивление единицы длины проводника 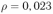 Ом/м. Найти величину и направление тока
Ом/м. Найти величину и направление тока 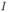 , текущего в проводнике при равномерном уменьшении поля до нуля в течение
, текущего в проводнике при равномерном уменьшении поля до нуля в течение 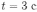 . Размеры отрезков проводника
. Размеры отрезков проводника 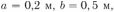
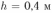 .
.
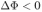 . Из закона электромагнитной индукции
. Из закона электромагнитной индукции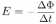
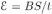 и сопротивления проводника
и сопротивления проводника 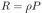 . Здесь
. Здесь 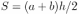 — площадь трапеции, а
— площадь трапеции, а 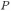
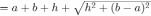 — ее периметр. Окончательно получаем:
— ее периметр. Окончательно получаем: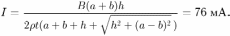
 одинаковых витков с площадью
одинаковых витков с площадью 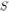 присоединена к баллистическому гальванометру. Вначале катушка находилась между полюсами магнита в однородном магнитном поле с индукцией
присоединена к баллистическому гальванометру. Вначале катушка находилась между полюсами магнита в однородном магнитном поле с индукцией 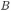 , параллельной оси катушки. Затем катушку переместили в пространство, где магнитное поле отсутствует. Какое количество электричества
, параллельной оси катушки. Затем катушку переместили в пространство, где магнитное поле отсутствует. Какое количество электричества 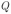 протекло через гальванометр? Сопротивление всей цепи
протекло через гальванометр? Сопротивление всей цепи 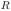 .
.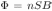 . Пусть катушка удаляется из магнитного поля за время
. Пусть катушка удаляется из магнитного поля за время 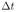 . Поскольку изменение магнитного потока за это время
. Поскольку изменение магнитного потока за это время 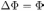 , величина ЭДС индукции
, величина ЭДС индукции 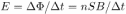 . Ток в цепи
. Ток в цепи 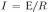 , протекший за время
, протекший за время 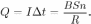 Это количество электричества и будет зарегистрировано баллистическим гальванометром, который измеряет прошедший через него заряд.
Это количество электричества и будет зарегистрировано баллистическим гальванометром, который измеряет прошедший через него заряд.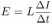 , где
, где 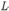 — индуктивность катушки. Поскольку
— индуктивность катушки. Поскольку 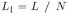 . Поэтому индукционный ток в витке
. Поэтому индукционный ток в витке 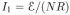 . Заряд, протекший через виток за время
. Заряд, протекший через виток за время 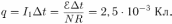
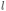 и соединенным сопротивлением R, под действием силы тяжести начинает скользить проводник, длина которого
и соединенным сопротивлением R, под действием силы тяжести начинает скользить проводник, длина которого 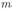 . Система находится в однородном магнитном поле, индукция которого
. Система находится в однородном магнитном поле, индукция которого 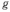 .
.
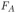 , которая, как нетрудно убедиться, будет направлена против скорости проводника. Таким образом, уравнение движения проводника запишется следующим образом:
, которая, как нетрудно убедиться, будет направлена против скорости проводника. Таким образом, уравнение движения проводника запишется следующим образом: 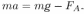
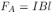 , а
, а 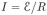 , где
, где 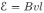 — ЭДС индукции, находим, что величина силы Ампера пропорциональна скорости проводника
— ЭДС индукции, находим, что величина силы Ампера пропорциональна скорости проводника 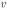 :
: 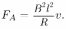
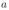 обратится в ноль, когда сила Ампера сравняется по величине с силой тяжести. Объединяя записанные выражения, находим, что скорость установившегося движения
обратится в ноль, когда сила Ампера сравняется по величине с силой тяжести. Объединяя записанные выражения, находим, что скорость установившегося движения 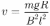 .
.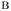 = 1 Тл, направленной вертикально вниз, по горизонтальным рельсам равномерно движется проводящий стержень длины
= 1 Тл, направленной вертикально вниз, по горизонтальным рельсам равномерно движется проводящий стержень длины 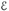 = 10, 1 В и внутренним сопротивлением
= 10, 1 В и внутренним сопротивлением  = 0, 1 Ом. Какое количество теплоты
= 0, 1 Ом. Какое количество теплоты 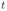 = 10 с, если его сопротивление
= 10 с, если его сопротивление 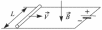
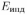 =
= 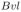 , направление которой, как нетрудно убедиться, при конкретных условиях задачи противоположно направлению ЭДС источника. По закону Ома для полной цепи индукционный ток
, направление которой, как нетрудно убедиться, при конкретных условиях задачи противоположно направлению ЭДС источника. По закону Ома для полной цепи индукционный ток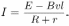
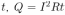 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 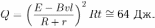
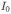 , текущего по длинному прямому проводу ОО’. Стороны AD и ВС параллельны проводу. Определить величину и направление тока, индуцированного в контуре в тот момент, когда сторона AD находится на расстоянии
, текущего по длинному прямому проводу ОО’. Стороны AD и ВС параллельны проводу. Определить величину и направление тока, индуцированного в контуре в тот момент, когда сторона AD находится на расстоянии 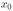 от провода. AD = ВС = а, АВ = DC = b. Сопротивление контура R.
от провода. AD = ВС = а, АВ = DC = b. Сопротивление контура R.
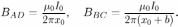
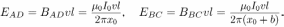
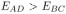 , поэтому суммарная работа сил Лоренца положительна при обходе контура по часовой стрелке. В этом же направлении будет течь индукционный ток, величина которого
, поэтому суммарная работа сил Лоренца положительна при обходе контура по часовой стрелке. В этом же направлении будет течь индукционный ток, величина которого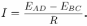
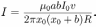
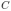 , может без трения двигаться проводник массой
, может без трения двигаться проводник массой 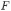 . Определить ускорение подвижного проводника. Сопротивлением реек и подводящих проводов пренебречь. В начальный момент скорость проводника равна нулю.
. Определить ускорение подвижного проводника. Сопротивлением реек и подводящих проводов пренебречь. В начальный момент скорость проводника равна нулю.
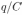 , где
, где 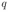 — заряд конденсатора. Индукционный ток
— заряд конденсатора. Индукционный ток 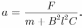
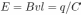 , ток в контуре
, ток в контуре 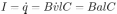 . Здесь точкой обозначена производная по времени и учтено, что ускорение проводника
. Здесь точкой обозначена производная по времени и учтено, что ускорение проводника 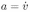 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 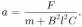
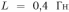 с сопротивлением обмотки
с сопротивлением обмотки 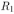 = 8 Ом к источнику с ЭДС
= 8 Ом к источнику с ЭДС 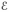 = 6 В и внутренним сопротивлением
= 6 В и внутренним сопротивлением 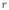 = 0,2 Ом. Какое количество тепла
= 0,2 Ом. Какое количество тепла 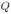 выделится в сопротивлении
выделится в сопротивлении 
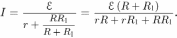
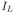 и
и 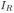 , протекающих, соответственно, через катушку и резистор
, протекающих, соответственно, через катушку и резистор 
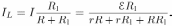
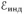 будет какое-то время поддерживать в цепи, образованной катушкой и резистором
будет какое-то время поддерживать в цепи, образованной катушкой и резистором 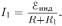
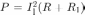 , выделяющаяся в этой цепи, распределится между катушкой и резистором пропорционально их сопротивлениям:
, выделяющаяся в этой цепи, распределится между катушкой и резистором пропорционально их сопротивлениям: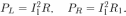
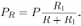
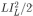 магнитного поля в катушке в момент отключения источника. Таким образом, количество тепла, выделившегося на резисторе
магнитного поля в катушке в момент отключения источника. Таким образом, количество тепла, выделившегося на резисторе