План урока
Тема: Логические операции и операции над множествами. Решение задач.
Планируемые образовательные результаты:
предметные - представления о разделе математики — алгебре логики, высказывании как ее объекте, об операциях над высказываниями и множествами;
метапредметные – навыки анализа логической структуры высказываний; понимание связи между логическими операциями и логическими связками, между логическими операциями и операциями над множествами;
личностные – понимание роли фундаментальных знаний как основы современных информационных технологий.
Решаемые учебные задачи:
знакомство с понятиями «пересечение» и «объединение» множеств;
отработка умений составления логических выражений, соответствующих сложным высказываниям;
отработка умений изображения множеств и отношений между ними с помощью кругов Эйлера.
Электронное приложение к учебнику:
презентация «Элементы алгебры логики»;
электронная тетрадь. 8 класс. ФГОС.
Ход урока
Приветствие, проверка присутствующих, наличия школьно-письменных принадлежностей, запись в тетрадях числа и темы урока.
Разбор нового материала.
Логические операции тесно связаны с операциями над множествами.
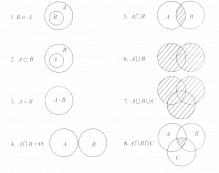
Пересечением множеств называется множество их общих элементов.
Объединением множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Пример 1. Рассмотрим два множества: A = { 1, 2, 3, 5, 7 }, B = { 1, 2, 3, 4, 6, 12, 18 }
C=A ∩ B Множество С является пересечением множеств A и B
C = { 1, 2, 3 }
Пример 2. Рассмотрим два множества: A = { 1, 5, 7, 9 }, B = { 1, 4, 5, 7 }
C=A ∩ B Множество С является пересечением множеств A и B
C = { 1, 5, 7 }
Пример 3. Найти пересечение следующих множеств:
A = { 1, 2, 3, 7, 9 }
B = { 1, 3, 5, 7, 9}
С = { 3, 4, 5, 8, 9}
A ∩ B ∩ C = D
D = { 3, 9}
Пример 4. Найти объединение следующих множеств:
A = { 1, 2 }
B = { 3, 5}
С = {8, 9}
A ∪ B ∪ C = D
D = { 1,2,3,5,8, 9}
Задача №1
Даны запросы к поисковому серверу:
1) бульдог & колли & уход
2) бульдог & колли
3) колли
4) бульдог | колли | уход
Изобразите графически количество страниц, которое найдёт поисковый сервер по каждому запросу. Расположите номера запросов в порядке убывания количества страниц, которые найдёт поисковый сервер по каждому запросу.
Задача №2
Даны запросы к поисковому серверу:
1) цветы & (весна | улыбки)
2) цветы | (весна & улыбки)
3) цветы | весна
4) весна | улыбки | цветы
Изобразите графически количество страниц, которое найдёт поисковый сервер по каждому запросу. Расположите номера запросов в порядке возрастания количества страниц, которые найдёт поисковый сервер по каждому запросу.
Учебник, стр.51
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | 4800 |
| Линкор | 4500 |
| Крейсер | Линкор | 7000 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?
Задача №4
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц(тыс.) |
| фрегат & эсминец | 500 |
| фрегат | 2000 |
| эсминец | 2500 |
Сколько страниц (в тысячах) будет найдено по запросу фрегат | эсминец?
Задача №5
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Сириус & Вега | 260 |
| Вега & (Сириус | Арктур) | 467 |
| Сириус & Вега & Арктур | 119 |
Какое количество страниц (в тысячах) будет найдено по запросу Вега & Арктур? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Задача №6
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Вагнер | 95 |
| Валькирия | 39 |
| Ника | 53 |
| Вагнер | Валькирия | Ника | 159 |
| Вагнер & Валькирия | 9 |
| Вагнер & Ника | 0 |
Какое количество страниц (в тысячах) будет найдено по запросу Валькирия & Ника?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Задача №7
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Кол-во страниц(тыс.) |
| Математика & Информатика | 330 |
| Математика & Физика | 270 |
| Математика & (Информатика | Физика) | 520 |
Какое количество страниц (в тысячах) будет найдено по запросу Математика & Информатика & Физика? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Практическая работа на ПК (электронная тетрадь, упр. 77-80)
Подведение итогов урока, выставление оценок
Домашнее задание: учебник, §2.2 читать, стр.58, упр.4-9 (письм).


















