ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ШКОЛА № 1 Г.О. ЕНАКИЕВО»
Учитель математики
Фоменко Н.Г.
Методы решения иррациональных неравенств.
Если в неравенство входят функции под знаком корня, то такие неравенства называют иррациональными.
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т. д. Однако, Правило : Если f (x) ≥ 0, g (x) ≥ 0 на множестве X, то неравенства
равносильны на этом множестве, преобразования неравенств, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны. При возведении же в квадрат неравенств, части которых имеют разные знаки, могут получиться неравенства, как равносильные исходному, так и неравносильные ему. Простой пример: –1  − тоже верное неравенство. Несмотря на то, что –4
− тоже верное неравенство. Несмотря на то, что –4  уже верным не является.
уже верным не является.
Как получить равносильные системы для некоторых часто встречающихся типов неравенств.
Неравенства вида: 
Если x лежит в ОДЗ: f (x) ≥ 0, то левая часть неравенства существует и неотрицательна. Поскольку для всех x, являющихся решением данного неравенства, правая часть больше левой, то g (x) 0. Следовательно, обе части неравенства неотрицательны (для тех x, которые являются решениями неравенства, другие x нас не интересуют). Значит, возведение в квадрат не нарушает равносильности и можно записать равносильную нашему неравенству систему неравенств:
Пример 1

Решение:
| Неравенство равносильно системе:
Ответ.  |
Пример 2
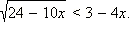
Решение:
|
Ответ. 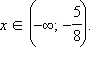 |
Неравенства вида 
ОДЗ данного неравенства f (x) ≥ 0. Пусть для каких-то x из ОДЗ g (x) x − решения, так как при этих x левая часть определена (x 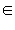 ОДЗ) и неотрицательна, в то время как правая часть g (x)
ОДЗ) и неотрицательна, в то время как правая часть g (x)
Для других x из ОДЗ g (x) ≥ 0. Для них обе части неравенства неотрицательны, и его можно возвести в квадрат:  Значит, данное неравенство равносильно совокупности неравенств:
Значит, данное неравенство равносильно совокупности неравенств:
Заметим, что в последнюю систему не входит требование f (x) ≥ 0. Оно и не нужно, так как выполняется автоматически 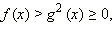 ибо полный квадрат всегда неотрицателен.
ибо полный квадрат всегда неотрицателен.
Пример 3
Решите неравенство 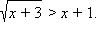
Решение:
| ОДЗ неравенства: x ≥ –3. 1. Если 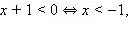 то все эти x то все эти x 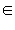 ОДЗ, для которых верно x ОДЗ, для которых верно x 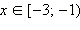 − первая часть ответа. − первая часть ответа. 2. Если 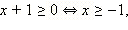 то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем: то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем: Получаем, что решениями являются все 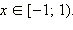 Объединяя результаты пунктов 1 и 2, получаем: Ответ. 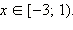 |
Пример 4
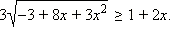
Решение:
Неравенства вида 
ОДЗ данного неравенства: 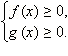 Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Заметим, что из неравенства  следует, что
следует, что 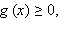 то есть дополнительно это требовать и включать это неравенство в систему не нужно.
то есть дополнительно это требовать и включать это неравенство в систему не нужно.
Отметим полезное следствие. Предположим, что ОДЗ неравенства уже найдено, и мы будем отбирать решения только из ОДЗ (это разумно, поскольку вне ОДЗ решений нет). Тогда исходное неравенство равносильно следующему:  а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде
а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде 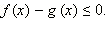 Следовательно, в ОДЗ
Следовательно, в ОДЗ
Эти же рассуждения применимы и для знака неравенства ≥. Отсюда можно сделать вывод:
Знак разности  совпадает со знаком выражения
совпадает со знаком выражения 
Отсюда же получается ещё одно следствие:
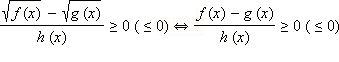 в ОДЗ:
в ОДЗ: 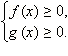
Пример 5
Решить неравенство: 
Перейдём к равносильной системе:
Решая эту систему методом интервалов, получаем:
Ответ. 
Пример 6
Решить неравенство. 
Решение:
ОДЗ неравенства: 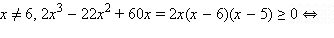
Заметим, что в ОДЗ x ≥ 0, поэтому существует 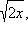 и значит,
и значит,
Мы воспользовались здесь тем, что в ОДЗ x ≥ 0, (x – 5)(x – 6) ≥ 0 и потому существуют выписанные в последней строчке корни. Кроме того, мы вынесли за скобку 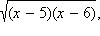 который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень
который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень 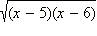 обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем:
обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем:
Учтём теперь ОДЗ и получим:
Ответ. 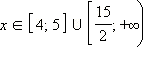
Неравенства вида 
ОДЗ данного неравенства:  Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство
Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство
|
| 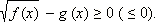
| (*) |
1. Если g (x) x из ОДЗ выполнено 
2. Если g (x) ≥ 0, то выражение  может иметь любой знак, но выражение
может иметь любой знак, но выражение 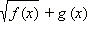 всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число
всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число 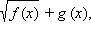 не меняя знака неравенства, перейдём к равносильному неравенству
не меняя знака неравенства, перейдём к равносильному неравенству
Таким образом, в ОДЗ
Значит, при g (x) ≥ 0, знак разности  совпадает со знаком разности
совпадает со знаком разности  в ОДЗ.
в ОДЗ.
Получаем следующие условия равносильности.
Запоминать приведённые системы неравенств не нужно, важно понимать, как они получаются.
Пример 7
Решить неравенство: 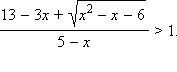
Решение:
Выполним равносильные в ОДЗ преобразования :.
Не случайно сделано последнее преобразование. Важно знать, чему конкретно равняется функция g (x) = 2x – 8. Часто ошибкой является считать, что g (x) = 2x + 8.
ОДЗ данного неравенства: 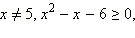 то есть
то есть 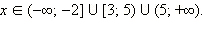 Перейдём к равносильной системе.
Перейдём к равносильной системе.
С учётом ОДЗ сразу получаем:
Ответ. 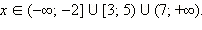
Вывод.
Иррациональными называются неравенства, в которых переменная содержится под знаком корня.
Иррациональное неравенство сводится к равносильной системе (или совокупности систем) неравенств:

Литература:
1.Математика: алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. организаций : базовый и углубленный уровни /( Ш.А. Алимов, Ю.М.Колягин и др.)-М. : Просвещение, 2023.
2.Дорофеев Г., Потапов М., Розов Н. Математика для поступающих в вузы. М.: Дрофа, 2002.







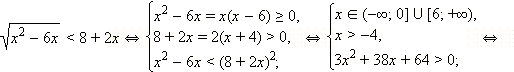
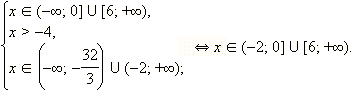

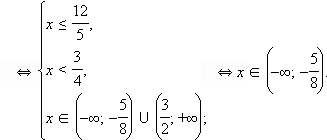
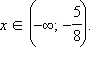

 Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.
Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства. то есть
то есть  то есть
то есть 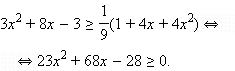
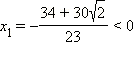 и
и 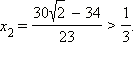 Значит, решением неравенства являются
Значит, решением неравенства являются  С учётом
С учётом 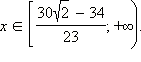 Объединяя результаты пунктов 1 и 2, получаем
Объединяя результаты пунктов 1 и 2, получаем
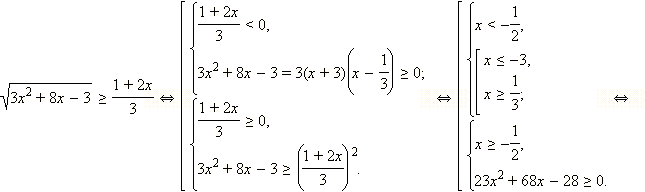

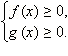 Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему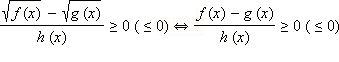 в ОДЗ:
в ОДЗ: 
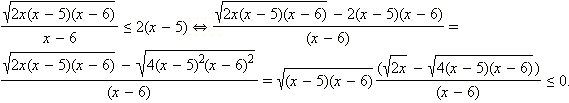

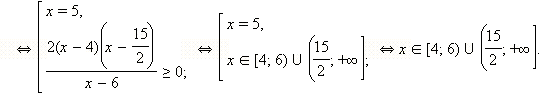
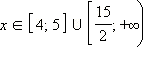

 Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство
Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство