| 2. Последовательность (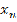 ) задана формулой: ) задана формулой: 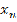 = =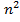 . Какой номер имеет член этой последовательности, если он равен 144? 225? 100? Являются ли членами этой последовательности числа 48? 49? 168? . Какой номер имеет член этой последовательности, если он равен 144? 225? 100? Являются ли членами этой последовательности числа 48? 49? 168? О последовательности (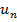 ) известно, что ) известно, что 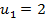 , , 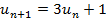 . Как называется такой способ задания последовательности? Найдите первые четыре члена этой последовательности. . Как называется такой способ задания последовательности? Найдите первые четыре члена этой последовательности. |
12, 25, 10
Нет, 49(да, 7), нет
Рекуррентный 2, 7, 22, 67 | Регулятивные (целеполагания) Коммуникативные |
| 3. Определение арифметической прогрессии: арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом: (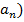 - арифметическая прогрессия, если - арифметическая прогрессия, если 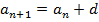 , где , где 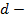 некоторое число. некоторое число. Число d, показывающее, на сколько следующий член последовательности отличается от предыдущего, называется разностью прогрессии: 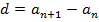 . . Давайте еще раз посмотрим на последовательности и поговорим о различиях. Какие особенности есть у каждой последовательности и с чем они связаны? Если в арифметической прогрессии разность положительна 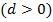 , то прогрессия является возрастающей: 2, 6, 10, 14, 18, :. ( , то прогрессия является возрастающей: 2, 6, 10, 14, 18, :. (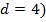 Если в арифметической прогрессии разность отрицательна (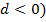 , то прогрессия является убывающей: 11, 8, 5, 2, -1, :. ( , то прогрессия является убывающей: 11, 8, 5, 2, -1, :. (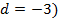 В случае, если разность равна нулю (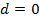 ) и все члены прогрессии равны одному и тому же числу, последовательность называется стационарной: 5, 5, 5, 5, :. ) и все члены прогрессии равны одному и тому же числу, последовательность называется стационарной: 5, 5, 5, 5, :.
Как задать арифметическую прогрессию? Рассмотрим следующую задачу. Задача. На складе 1 числа было 50 тонн угля. Каждый день в течение месяца на склад приходит машина с 3 тоннами угля. Сколько угля будет на складе 30 числа, если в течение этого времени уголь со склада не расходовался. Если выписать количество угля, находящегося на складе каждого числа, получим арифметическую прогрессию. Как решить эту задачу? Неужели придется просчитывать количество угля в каждый из дней месяца? Можно ли как-то обойтись без этого? Замечаем, что до 30 числа на склад придет 29 машин с углем. Таким образом, 30 числа на складе будет 50+3 29=137 тонн угля. 29=137 тонн угля. Таким образом, зная только первый член арифметической прогрессии и разность, мы можем найти любой член последовательности. Всегда ли это так? Проанализируем, как зависит каждый член последовательности от первого члена и разности: 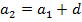
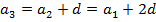
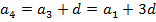
::::::::::::: 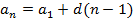
Таким образом, мы получили формулу n-ого члена арифметической прогрессии.
Пример 1. Последовательность (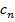 )-арифметическая прогрессия. Найдите )-арифметическая прогрессия. Найдите 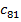 , если , если 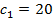 и и 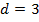 . .
Рассмотрим следующую задачу: В арифметической прогрессии четные члены оказались затерты: 3, :, 7, :, 13: Можно ли восстановить утраченные числа? Решение: Воспользуемся тем, что в арифметической прогрессии разность между соседними членами постоянна. Пусть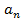 - искомый член последовательности. Тогда - искомый член последовательности. Тогда 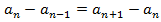 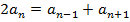
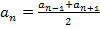 . .
Замечание. Данное свойство арифметической прогрессии является ее характеристическим свойством. Это означает, что в любой арифметической прогрессии каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего ( 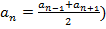 . И, наоборот, любая последовательность, в которой каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего, является арифметической прогрессией. . И, наоборот, любая последовательность, в которой каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего, является арифметической прогрессией.
| Конспектируют основные моменты
Воспользуемся формулой n-ого члена 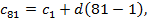 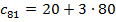 , , 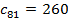 Ответ: 260.
5, 10
| Коммуникативные
Регулятивные |
| 4. Задача. Числовая последовательность задана формулой 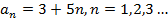 Является ли эта последовательность арифметической прогрессией? Решение. Поскольку 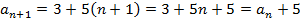 , при всех значениях n, то последовательность является арифметической прогрессией по определению. Из полученной формулы , при всех значениях n, то последовательность является арифметической прогрессией по определению. Из полученной формулы 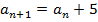 разность этой прогрессии равна 5. разность этой прогрессии равна 5. Ответ: является. Задача. Седьмой член арифметической прогрессии равен 1 и равен разности между четвертым и вторым членами. Найти первый член прогрессии. Решение. По условию 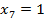 , , 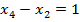 . Заметим, что . Заметим, что 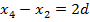 , откуда , откуда 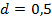 . . По формуле n-ого члена 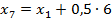 , откуда , откуда 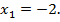 Ответ: -2. | Решение задач №575 10 14 18 22 26 30 20 10 0 -10 №576 B1+6d; B1+230d B1+(k+4)d №577 -24,2. №580 25 | Регулятивные Коммуникативные |


















