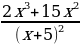ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ МОСКОВСКОЙ ОБЛАСТИ
«Профессиональный колледж «Московия»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ОТКРЫТОЕ МЕРОПРИЯТИЕ ПО МАТЕМАТИКЕ:
Открытый урок по теме «Правила нахождения производной»
Разработчики:
1. Кулакова Н.И., преподаватель математики, ГАПОУ МО «Профессиональный колледж «Московия»,
2025
Цель: формировать у студентов целостное представление о производной
Задачи:
-образовательная: знать правила нахождения производной, применять правила нахождения производной при решении упражнений
-развивающая: развивать аналитико-синтетические способности
-воспитательная: воспитывать трудолюбие и усидчивость.
Ход урока
Организационный момент.
Мотивация.
- вычисление мгновенной скорости
- Мы умеем находить производную функции f(x) = 2x- 10, а как находить производную функции f(x)= (2x – 10) 
Основной этап. Объяснение нового материала.
Правило 1.
Если функции u и v дифференцируемы в точке х0 , то их сумма дифференцируема в этой точке и
(u+v)’ = u’ + v’
Производная суммы равна сумме производных.
Правило 2.
Если функция u и v дифференцируемы в точке х0 ,то их произведение дифференцируемо в этой точке и
(uv)’ = u’v + uv’
Следствие
Если функция u дифференцируемы в точке х0 , а С – постоянная, то функция Cu дифференцируема в этой точке и
(Cu)’ = Cu’
Постоянный множитель можно выносить за знак производной
Правило 3.
Если функция u и v дифференцируемы в точке х0 , и функция v не равна нулю в этой точке, то их частное дифференцируемо в этой точке и
(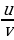 )’ =
)’ = 
Нахождение производной степенной функции
Мы знаем производную функций y= x2 y’= 2x; y =x3 y’= 3x2, по аналогии попробуйте найти производные функций f(x) = x4 ; f(x) = x8; f(x) = x2025
Отсюда следует формула нахождения производной степенной функции
(xn)’ = nxn-1
Рассмотрим примеры.
Задание – найти производную.
f(x) = 3x3 + 5x2 – 6x + 7
f’(x) = 3(x3)’ + 5(x2)’ – 6(x)’ + 7’ = 3*3x2 + 5*2x – 6*1 + 0 = 9x2 +10x - 6
f(x) = (4x2 – 6) 
f’(x) = (4x2 – 6)’* + (4x2 – 6) *(
+ (4x2 – 6) *( )’ = 8x*
)’ = 8x* +(4x2 - 6)*
+(4x2 - 6)* 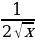 = 8x*
= 8x* +
+ 
f(x) = 
f’(x) =  =
=  =
= 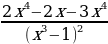 =
= 
y= 3x7 - 
y’ = 3(x7)’ -5(x-3)’ = 3*7x6 – 5*(-3x-4) = 21x6 +15x-4 = 21x6 + 
Первичное закрепление,
Устно
Найти производную
- 5х2 + 6х
-  *(2х-1)
*(2х-1)
- 7x11 +1
Закрепление материала.
Разделиться на группы по рядам на 3 группы
Решаем по примеру, потом проверяем на доске
Задание для первой группы:
Найти производную
f(x) = x2 + x3
f(x) =  * (2x2 – x)
* (2x2 – x)
f(x) =
y= x8 -3x4 + 
Задание для второй группы
f(x) =  +5x -2
+5x -2
f(x) = x2*(4 + 2x –x2)
f(x) = 
y=  -
- 
Задание для третьей группы
f(x) = x2 +3x -1
f(x) = x2 (3x + x3)
f(x) = 
y= x7 – 4x5 + 
Подведение итогов.
Решение с комментированием
Вычислить значение производной в точке
f(x) = x2 -3x, x = - , x = 2
, x = 2
Решение всей группой с последующей проверкой
Решите уравнение f’(x) = 0, если f(x) = 2x2 – x
Одновременно индивидуально решают четыре ученика, потом демонстрируют решение группе
-Решите неравенство f’(x) f(x) = 4x -3x2
- Найдите производную функции
f(x) = 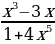
Проведение тестирования
Вариант 1
1. Найдите производную функции f(x) = 3x2 + 5x - 2.
a) 6x + 5
b) 3x + 5
c) 6x - 5
d) 3x - 5
2. Найдите производную функции f(x) = 
a) 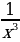
b) 
c) 
d) 
3. Найдите производную функции f(x) = (x+1)(x-2).
a) 2x +3
b) 2x + 1
c) 2x - 3
d) 2x -1
4. Найдите производную функции f(x) =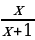 .
.
a) 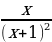
b) 
c) 
d) 
5. Найдите производную функции f(x) =  .
.
a) 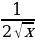
b) 
c)  .
.
d) 2 .
.
6. Найдите производную функции f(x) = 
a) -
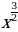
b) -

c) -
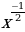
d) -

7. Найдите производную функции f(x) = 
a) 
b) 
c)
d) 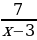
8. Найдите производную функции f(x) = x3 – 2x2 + x - 1.
a) 3x2 +4x + 1
b) 3x2 - 4x - 1
c) 3x2 + 4x + 1
d) 3x2 - 4x + 1
9. Найдите производную функции f(x) = 
a) 
b) 
c) 
d) 
10. Найдите производную функции f(x) = 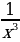
a) 
b) 
c) 
d) 
Ответы Варианта 1:
1. a) 2. c) 3. d) 4. c) 5. a) 6. b) 7. b) 8. d) , 9. d), 10. a)
Вариант 2
1. Найдите производную функции f(x) = 2x3 - 3x2 + 4x - 5.
a) 6x2 - 6x - 4
b) 6x2 - 6x + 4
c) 6x2 + 6x + 4
d) 6x2 + 6x - 4
2. Найдите производную функции f(x) =  .
.
a) 
b) 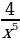
c) 
d) 
3. Найдите производную функции f(x) = (x-1)(x+3).
a) 2x - 2
b) 2x + 2
c) 2x + 4
d) 2x - 4
4. Найдите производную функции f(x) =  .
.
a) 
b) 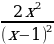
c) 
d) 
5. Найдите производную функции f(x) =  .
.
a) 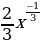
b) 
c) 
d) 
6. Найдите производную функции f(x) = 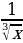 .
.
a) -
b) -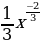
c) -
d) -
7. Найдите производную функции f(x) =  .
.
a) 
b) 
c) 
d) 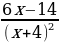
8. Найдите производную функции f(x) = x4 - 3x3 + 2x2 - x + 6.
a) 4x3 + 9x2 + 4x - 1
b) 4x3 - 9x2 - 4x - 1
c) 4x3 - 9x2 + 4x - 1
d) 4x3 - 9x2 + 4x + 1
9. Найдите производную функции f(x) = 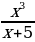 .
.
a) 
b) 
c) 
d) 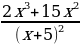
10. Найдите производную функции f(x) =  .
.
a) 
b) 
c) 
d) 
Ответы Варианта 2
b) 2. a) 3. b) 4. d), 5. a) 6. c) , 7. b) 8. c) 9. d) 10. b)
Подведение итогов. Домашнее задание
- что нового узнали на уроке
-чему новому научились на уроке
-что не получилось
- какие цели на следующий урок, на выполнение домашнего задания
Рациональная оценка
| Анализ действий | Степень достижения результата | Программа последующих действий |
| Сегодня я узнал | Теперь я могу… | Я попробую... |
| Я выполнял задания (какие?)... | Я приобрел... | Урок дал мне для жизни... |
| Я понял, что... | У меня получилось… | Мне захотелось..
|
Алгебра и начала анализа 10-11 класс А.Н.Колмогоров и др
Прочитать стр 113-116
Решить №208-214(г)







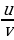 )’ =
)’ = 
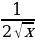 = 8x*
= 8x*

 =
=  =
= 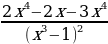 =
= 


 *(2х-1)
*(2х-1) 

 +5x -2
+5x -2
 -
- 


 , x = 2
, x = 2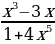

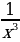


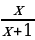 .
.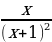




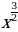

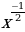





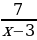










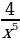


 .
.
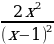


 .
.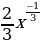



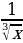 .
.
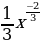


 .
.


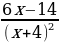
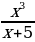 .
.