Презентация по геометрии " Обобщение по теме треугольники"

Треугольник

Один мудрец сказал: «Высшее проявление духа- это разум. Высшее проявление ума- это геометрия. Клетки геометрии- это треугольник. Он так же неисчерпаем, как и Вселенная».

Выполнила: Ученица 9 класса Б Гимназии им.А.Л. Кекина Лавриненко Вера

Цели и задачи:

• Узнать мини историю о треугольнике
• Обобщить теоретический материал
• Увидеть несколько набор задач

История треугольника

Треугольник – простейшая плоская фигура. Три вершины, три стороны. Но изучение треугольника породило целую науку – тригонометрию.

Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. В Древней Греции изучение свойств треугольника достигает высокого уровня – это теорема Пифагора и формула Герона, которым более 2000 лет.

• Треугольник – простейшая плоская фигура. Три вершины, три стороны. Но изучение треугольника породило целую науку – тригонометрию. Первые упоминания о треугольнике и его свойствах ученые находят в египетских папирусах, которым более 4000 лет. В Древней Греции изучение свойств треугольника достигает высокого уровня – это теорема Пифагора и формула Герона, которым более 2000 лет.

Задача 1

• Точка E лежит на стороне AC треугольника ABC, причём ECAE=2. Точка D лежит на BC, причём ED∥AB. Найдите AB, если ED=43.
• Решение: Так как ED∥AB, то ∠CED=∠CAB, ∠CDE=∠CBA (как соответственные при параллельных прямых и секущей), тогда треугольники CED и CAB подобны. Так как EC=2⋅AE, то AC=3⋅AE, следовательно, AC : EC = (3⋅AE) : (2⋅AE) = 3:2. Так как стороны EC и AC лежат против равных углов (в треугольниках CED и CAB соответственно), то AB : ED = AC : EC = 3:2, откуда AB = 3:2⋅ED = 3:2⋅4:3 = 2.

Ответ: 2

Задача 2

• F – точка пересечения AD и BE – медиан треугольника ABC. Известно, что S Δ ABF=1. Найдите S Δ DEF.средняя линия треугольника ABC, тогда ED=0,5⋅AB, ED∥AB.

Решение: ED - средняя линия треугольника ABC, тогда ED=0,5⋅AB, ED∥AB.

• Так как ED∥AB, то ∠DEF=∠ABF, ∠EDF=∠FAB (как внутренние накрест лежащие при параллельных прямых и секущей), следовательно, треугольники DEF и ABF подобны (по двум углам). Так как ED=0,5⋅AB, причём стороны ED и AB лежат (в треугольниках DEF и ABF соответственно) против равных углов,то S Δ DEF : S Δ ABF =(ED : AB) ² =0,5 ² =0,25, откуда с учётом того, что S Δ ABF=1 находим S Δ DEF=0,25.

Ответ: 0,25

Задача 3

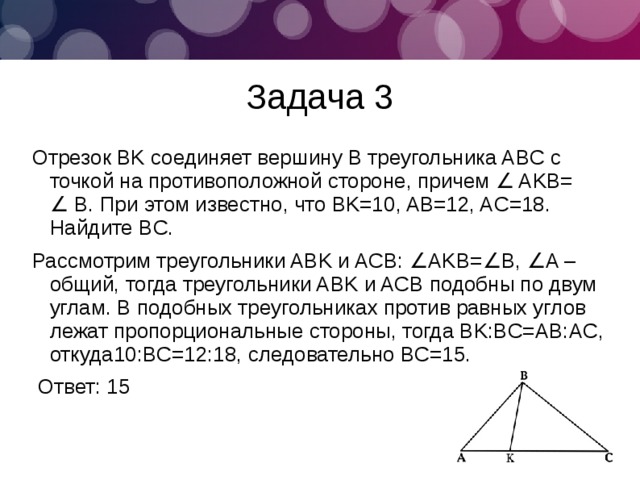
Отрезок BK соединяет вершину B треугольника ABC с точкой на противоположной стороне, причем ∠ AKB= ∠ B. При этом известно, что BK=10, AB=12, AC=18. Найдите BC.

Рассмотрим треугольники ABK и ACB: ∠AKB=∠B, ∠A – общий, тогда треугольники ABK и ACB подобны по двум углам. В подобных треугольниках против равных углов лежат пропорциональные стороны, тогда BK:BC=AB:AC, откуда10:BC=12:18, следовательно BC=15.

Ответ: 15

Задача 4

На сторонах AB, BC и AC треугольника ABC лежат точки D, E и F соответственно. Известно, что DF:BC=0,5, AC=2⋅DE, AB−EF=EF ∠ DEF=61 ° , ∠ EFD=55 ° . Найдите ∠ C. Ответ дайте в градусах.

Так как ∠ DEF=61 ° , ∠ EFD=55 ° , то ∠EDF=180 ° −61 ° −55 ° =64 ° . Рассмотрим треугольники ABC и EFD: по условию DF:BC=0,5=DE:AC=EF:AB, тогда треугольники ABC и EFD подобны по пропорциональности трех сторон. В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда ∠C=∠EDF=64 °.

Ответ: 64

Ссылки

• https://shkolkovo.net/catalog/planimetriya_chast_i/treugolnik_zadachi_na_podobie
• © shkolkovo.net
• https://pandia.ru/text/79/432/23526.php
• https://ru.wikipedia.org/wiki/Треугольник#История_изучения