Презентация по теме "Четырёхугольники"

Повторение.

Четырехугольники.

Параллелограмм

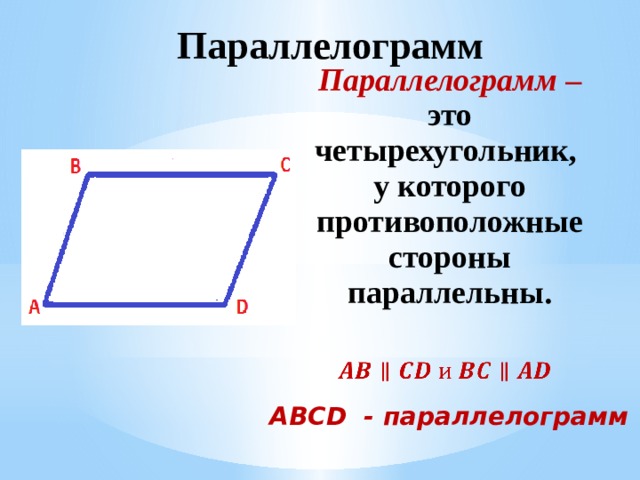
Параллелограмм – это четырехугольник,

у которого противоположные стороны параллельны.

ABCD - параллелограмм

Свойства углов параллелограмма

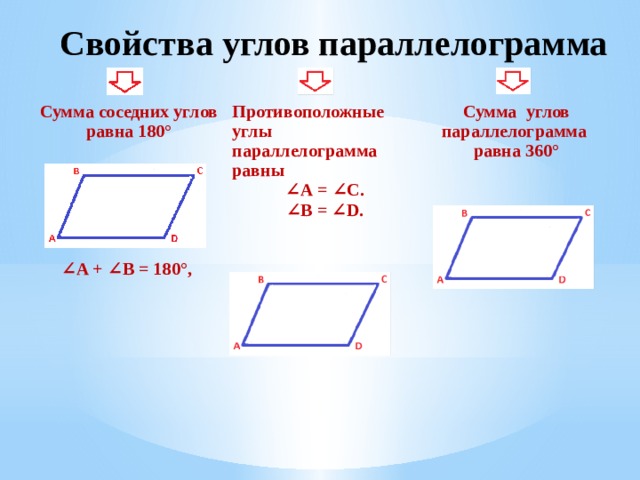
Сумма соседних углов равна 180°

Противоположные углы параллелограмма равны

∠ А = ∠С.

Сумма углов параллелограмма равна 360°

∠ B = ∠D.

∠ A + ∠B = 180°,

Свойство сторон параллелограмма

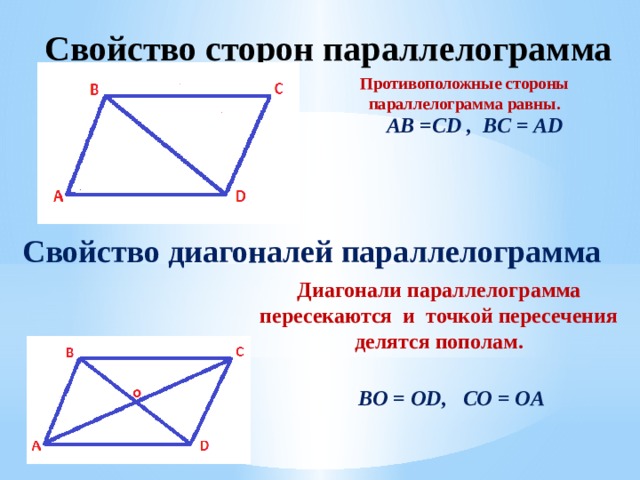
Противоположные стороны параллелограмма равны.

AB =CD , BC = AD

Свойство диагоналей параллелограмма

BO = OD, CO = OA

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Решение задач

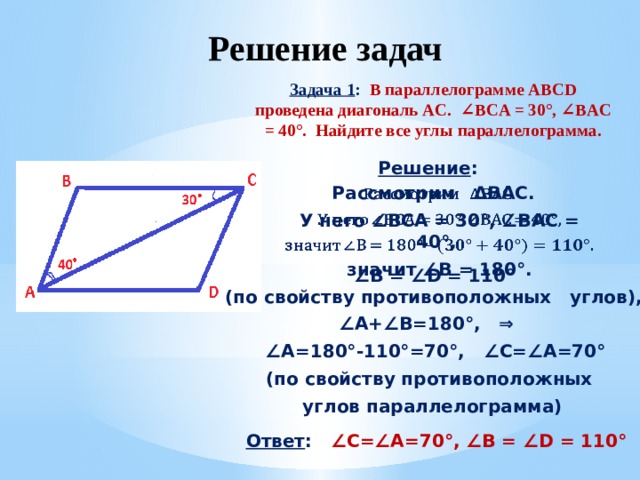
Задача 1 : В параллелограмме ABCD проведена диагональ AC. ∠BCA = 30°, ∠BAC = 40°. Найдите все углы параллелограмма.

Решение :

Рассмотрим ΔBAC.

У него ∠BCA = 30°, ∠BAC = 40°,

значит ∠B = 180° .

∠ B = ∠D = 110°

(по свойству противоположных углов),

∠ A+∠B=180°, ⇒

∠ A=180°-110°=70°, ∠C=∠A=70°

(по свойству противоположных

углов параллелограмма)

Ответ : ∠C=∠A=70°, ∠B = ∠D = 110°

Решение задач

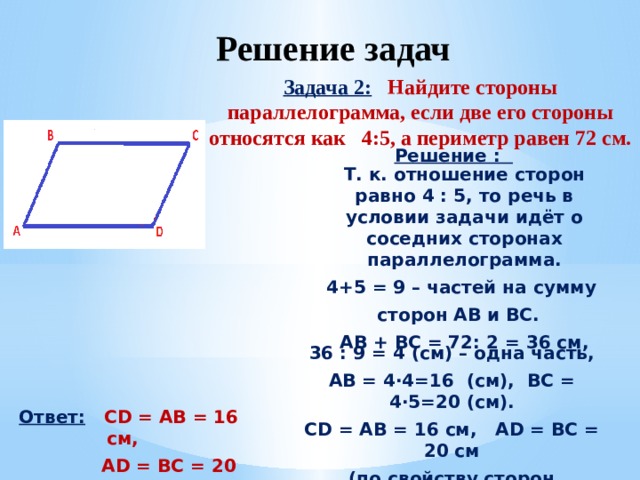
Задача 2: Найдите стороны параллелограмма, если две его стороны относятся как 4:5, а периметр равен 72 см.

Решение :

Т. к. отношение сторон равно 4 : 5, то речь в условии задачи идёт о соседних сторонах параллелограмма.

4+5 = 9 – частей на сумму

сторон AB и BC.

AB + BC = 72: 2 = 36 см,

36 : 9 = 4 (см) – одна часть,

AB = 4·4=16 (см), BC = 4·5=20 (см).

CD = AB = 16 см, AD = BC = 20 см

(по свойству сторон параллелограмма)

Ответ: CD = AB = 16 см,

AD = BC = 20 см

Решение задач

Задача 3 : В параллелограмме ABCD проведена биссектриса угла А. Она разбивает сторону ВС на отрезки BH =6 см и HC =4 см. Найдите периметр параллелограмма.

Решение :

∠ 3=∠2, т.к. АH – биссектриса,

∠ 1=∠3 (накрест лежащие

при BC∥AD и секущей AH), ⇒ ∠1=∠2,

ΔABH – равнобедренный ( по признаку),

⇒ AB = BH = 6cм.

BC = AD = 10 cм, AB = CD = 6 cм.

Р = 2·(10+6) = 32 см.

Ответ : P=32 см.

Решение задач

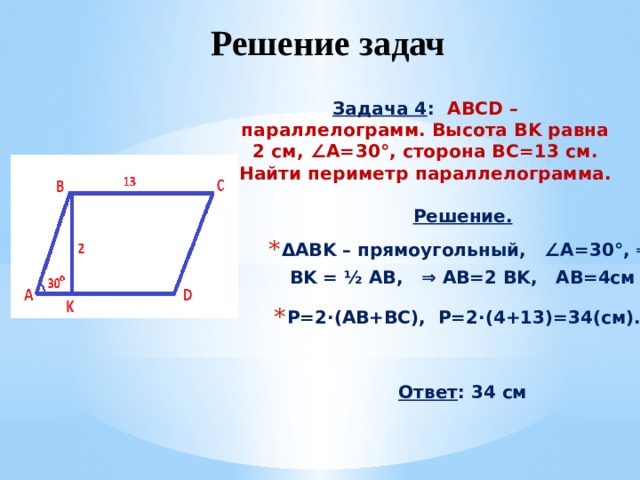
Задача 4 : ABCD – параллелограмм. Высота BK равна 2 см, ∠A=30°, сторона BC=13 см. Найти периметр параллелограмма.

Решение.

• ΔABK – прямоугольный, ∠A=30°, ⇒

BK = ½ AB, ⇒ AB=2 BK, AB=4см

• P=2· (AB+BC), Р=2·(4+13)=34(см).

Ответ : 34 см

Устное решение задач

Задача: ABCD – параллелограмм. Найти углы C и D.

Ответ: ∠C=64°,∠D=116°.

Устное решение задач

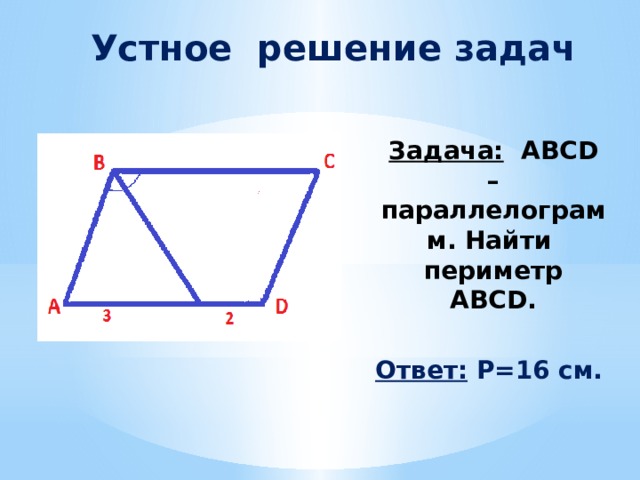
Задача: ABCD – параллелограмм. Найти периметр ABCD.

Ответ: Р=16 см.

Прямоугольник

Прямоугольник – это параллелограмм, у которого все углы прямые.

∠ A=∠B=∠C=∠D=90°

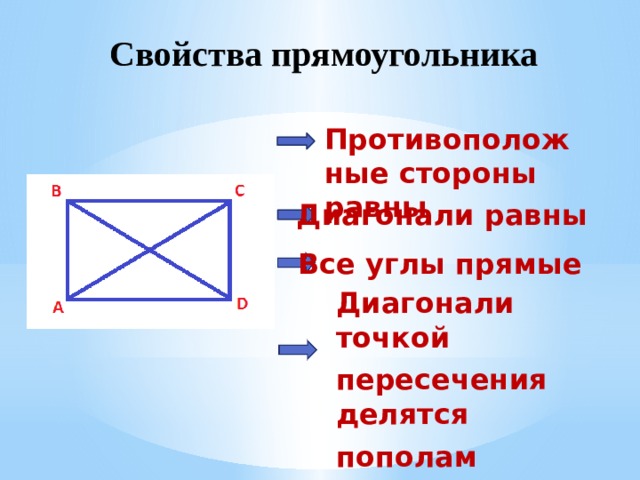
Свойства прямоугольника

Противоположные стороны равны

Диагонали равны

Все углы прямые

Диагонали точкой

пересечения делятся

пополам

Решение задач

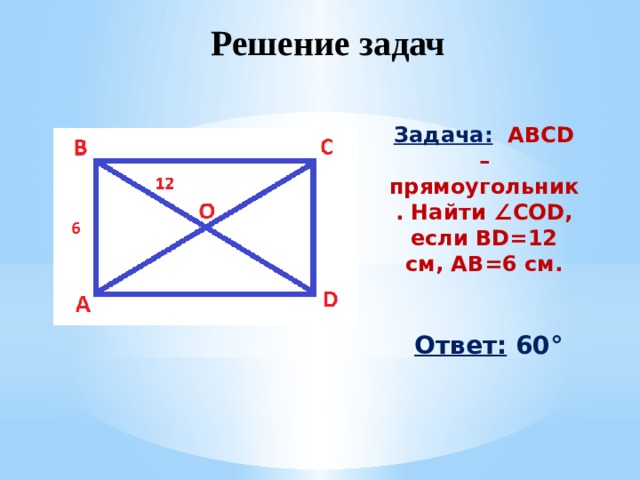
Задача: ABCD – прямоугольник. Найти ∠COD, если BD=12 см, AB=6 см.

Ответ: 60°

Решение задач

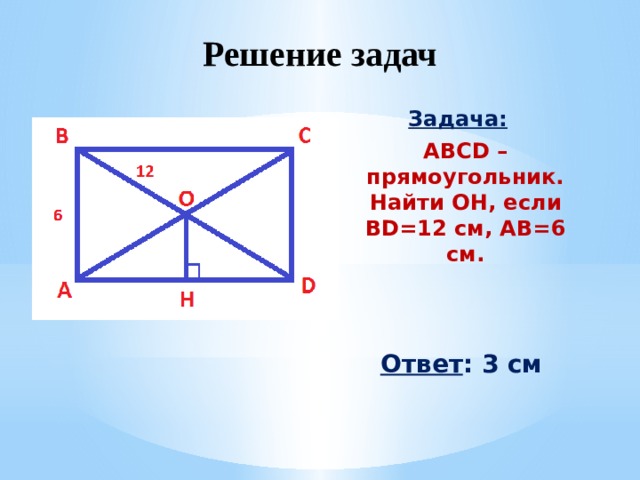
Задача:

ABCD – прямоугольник. Найти OН, если BD=12 см, AB=6 см.

Ответ : 3 см

Решение задач

Задача:

ABCD – прямоугольник. АК – биссектриса ∠A, СК=2,7 см, КD =4,5 см. Найти периметр ABCD.

Ответ : Р=23,4 см

Ромб

Ромб – это параллелограмм, у которого все стороны равны.

A B=BC=CD=DA

Свойства ромба

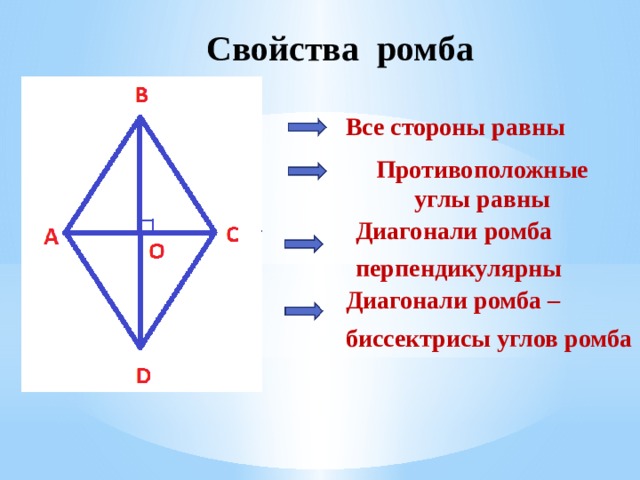
Все стороны равны

Противоположные углы равны

Диагонали ромба

перпендикулярны

Диагонали ромба –

биссектрисы углов ромба

Решение задач

Задача:

ABCD – ромб. Найдите углы ромба, если сторона АВ ромба образует с диагоналями углы 70 °,2O°.

Ответ : 40°,40°,14O°,14O°

Ромб. Решение задач

Задача:

ABCD – ромб.

Найти ∠С.

Ответ: 70°

Квадрат

Квадрат –

это прямоугольник,

у которого все стороны

равны.

AB = BC = CD = DA

Квадрат. Свойства квадрата

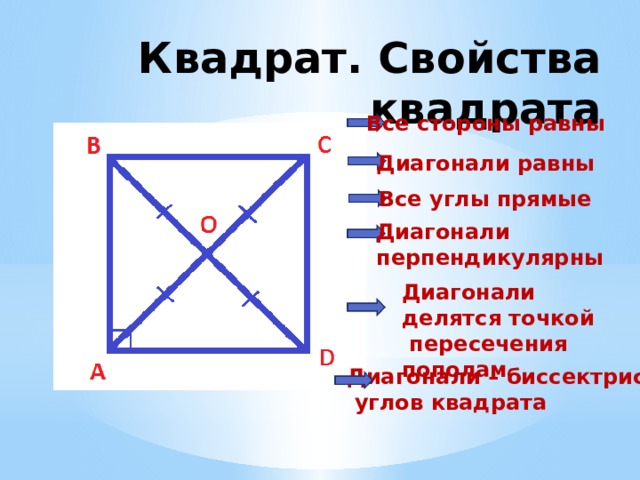
Все стороны равны

Диагонали равны

Все углы прямые

Диагонали

перпендикулярны

Диагонали делятся точкой

пересечения пополам

Диагонали – биссектрисы

углов квадрата

Боковая сторона

Боковая сторона

Трапеция

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Основание

Основание

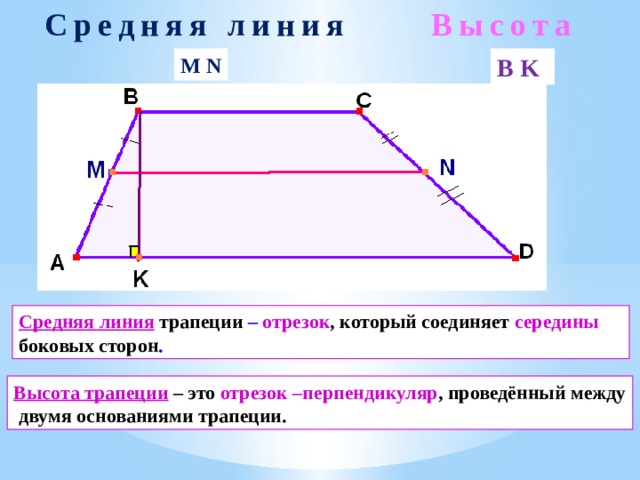
Средняя линия

Высота

M N

B K

Средняя линия трапеции – отрезок , который соединяет середины боковых сторон .

Высота трапеции – это отрезок –перпендикуляр , проведённый между двумя основаниями трапеции.

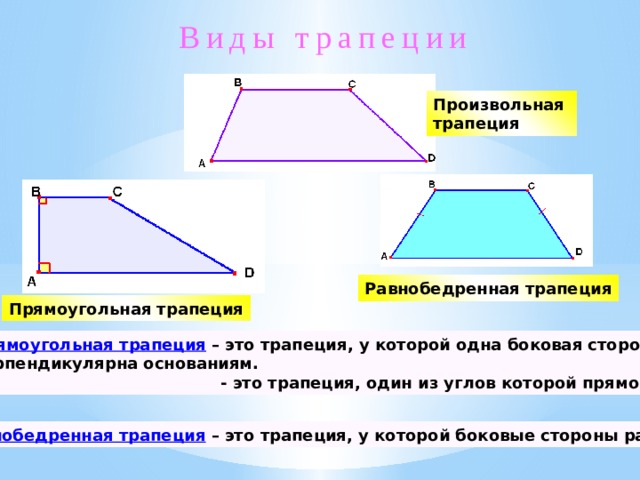
Виды трапеции

Произвольная трапеция

Равнобедренная трапеция

Прямоугольная трапеция

Прямоугольная трапеция – это трапеция, у которой одна боковая сторона перпендикулярна основаниям.

- это трапеция, один из углов которой прямой

Равнобедренная трапеция – это трапеция, у которой боковые стороны равны

Решение задач

АВСD – трапеция, ∠A = 36 °, ∠C = 117 °

∠ В = ?, ∠D = ?

С

Решение

В

АВСD – трапеция, то ВС ∥ AD.

117 °

∠ А + ∠В = 180°

36 ° + ∠В = 180°

∠ В = 180° - 36 °

D

А

36 °

∠ В = 144 °

∠ С + ∠D = 180°

∠ 117 ° + ∠D = 180°

∠ D = 180° - ∠117 °

∠ D = 63 °

∠ В = 144 °,

∠ D = 63 °

Ответ:

Задача

АВСD – равнобокая трапеция, ∠A = 68 °,

∠ В = ?, ∠С -?, ∠D = ?

Решение

С

В

Если АВСD – равнобокая трапеция ,

то ∠A = ∠D = 68°,

∠ 68 ° + ∠В = 180°

68 °

68 °

∠ В = 180° - ∠ 68 °

D

А

∠ В = 112°

∠ В = ∠С = 112°,

Ответ:

∠ С = 112°.

D = 68°,

∠ В = 112°,

Задача

Найдите основание AD равнобедренной трапеции ABCD , если ВС = 10 см, АВ = 12 см,

 D = 60 0

Ответ: 22