ПЛАН САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
Раздел 1. АЛГЕБРА
Тема 1.3. Основы тригонометрии
Задание 1. Заполнение карты формулами и определениями.
Указания: распечатать и заполнить карту (на карте подписать фамилию и группу)
| Определение синуса, косинуса, тангенса и котангенса. | Синус - Косинус - тангенс - котангенс –
|  |
| Знаки синуса 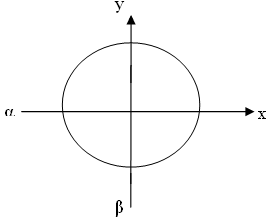
| Знаки косинуса 
| Знаки тангенса и котангенса 
|
| Четность и нечетность функций у=sin x, y=cos x, y=tg x, y=ctg x.
| Функция у=sin x –
Функция y=cos x - | Функция y=tg x -
Функция y=ctg x - |
| Период функций | у=sin x, y=cos x
Т= | y=tg x, y=ctg x
Т= |
| Радианная мера угла. Выразить в радианной мере величины углов | | 300 = | 900 = | 3600 = | | 600 = | 1800 = |
| | 450 = | 2700 = |
|
|
|
| Отметить на единичной окружности точки, соответствующие углам | 0°, 90°, 270°, 180°, 360° 
| 0, π/2, π, 3π/2, 2π 
|
| Соотношения между тригонометрическими функциями одного и того же угла. | Основные тригонометрические тождества: 1 2 3 4
|
| Формулы приведения. | Выражение тригонометрических функций углов вида
через функции угла  |
| Формулы сложения. | cos (α + β)= cos (α — β)= 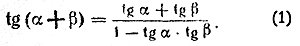
| sin (α + β) = sin (α — β) = 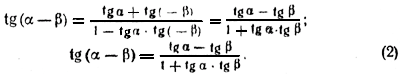
|
| Формулы двойного угла. | 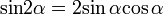
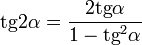
| 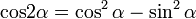
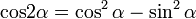
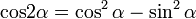
|
| Формулы суммы и разности тригонометрических функций. | 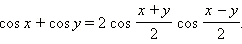
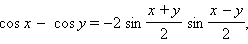
| 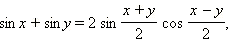
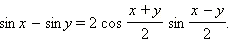
|
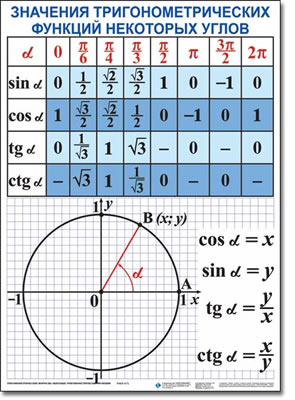
| Формулы преобразования произведения тригонометрических функций в сумму. | 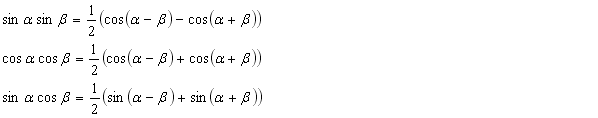
|
| Формулы половинного аргумента. | 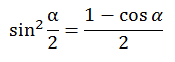
| 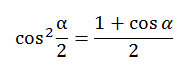
|
| Теорема косинусов |
|
| Теорема синусов |
|
| Соотношения в прямоугольном треугольнике
| 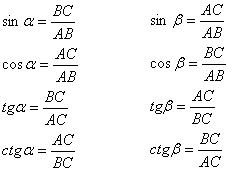 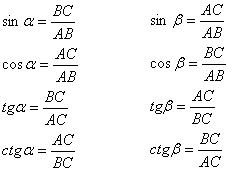 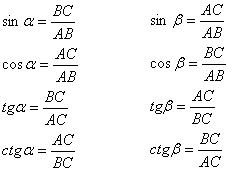 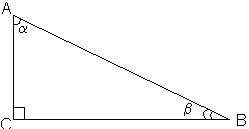 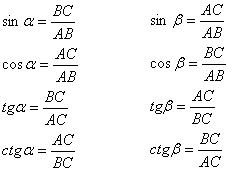 |
Задание 2. Подготовка сообщений, докладов и презентаций.
Рекомендуемые темы:
История тригонометрии
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических неравенств
Задание 3. Изучение приемов вычислений тригонометрических выражений на калькуляторе.
Отчет о выполненной работе должен содержать печатную копию электронного документа с указанием фамилии, группы студента, времени выполнения, названия, цели работы, выполненные задания описательной части работы.
Цель работы: изучить приемы выполнения тригонометрических выражений в программе "Калькулятор", входящей в состав стандартных программ ОС Windows.
Порядок выполнения работы
"Калькулятор" предоставляет возможности для вычисления значений некоторых тригонометрических функций, в т. ч. обратных. Подобные расчёты осуществляются только после установки инженерного вида.
Из числа тригонометрических функций "напрямую" "Калькулятор" позволяет определить значения синуса ( ), косинуса (
), косинуса ( ) и тангенса (
) и тангенса (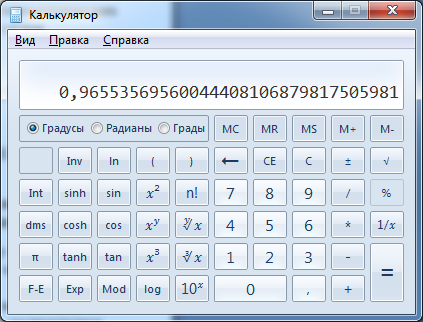 ). Аргументами этих функций являются величины, описывающие углы, поэтому для выражающих эти величины чисел следует устанавливать единицы измерения углов. Определим, какие единицы измерения углов доступны для использования в "Калькуляторе".
). Аргументами этих функций являются величины, описывающие углы, поэтому для выражающих эти величины чисел следует устанавливать единицы измерения углов. Определим, какие единицы измерения углов доступны для использования в "Калькуляторе".
✦ Угол величиной 1 радиан — центральный, опирающийся на дугу, длина которой составляет 1/2π длины всей окружности.
✦ Угол величиной 1 градус — центральный, опирающийся на дугу, длина которой составляет 1/360 длины всей окружности.
✦ Угол величиной 1 град — центральный, опирающийся на дугу, длина которой составляет 1/400 длины всей окружности.
При установке единиц измерения углов будем пользоваться соответствующими радиокнопками, пиктограммы которых будут присутствовать в наших программах: 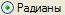 для установки радиан,
для установки радиан,  — градусов и
— градусов и  — град.
— град.
Пример 1 показывает, что основное тригонометрическое тождество справедливо при любых значениях угла, для которого вычисляются используемые в нём тригонометрические функции.
Задача 1. Показать, что sin2 50° + cos2 50° = 1.
Решение. Выполним решение по программе:



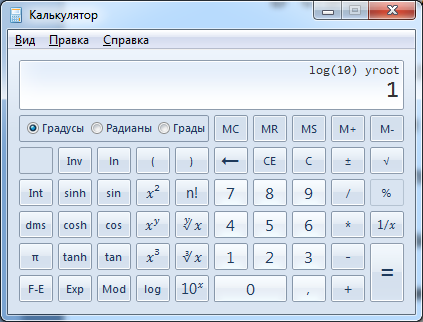





 1.
1.
В Примере 2 произведены последовательные вычисления тригонометрических функций с аргументами, выраженными разными единицами измерения углов.
Задача 2. Вычислить: cos π/12 – tg4 8°.
Решение.
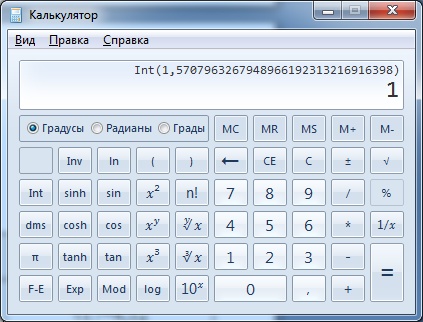



 0,26179938779914943653855361527329
0,26179938779914943653855361527329
 0,9659258262890682867497431997289
0,9659258262890682867497431997289


 0,14054083470239144683811769343281
0,14054083470239144683811769343281


 0,96553569560044408106879817505981.
0,96553569560044408106879817505981.
Обратные тригонометрические функции можно вычислить, устанавливая кнопку функционального модификатора 'Inv'. Так, арксинус определяется благодаря сочетанию 
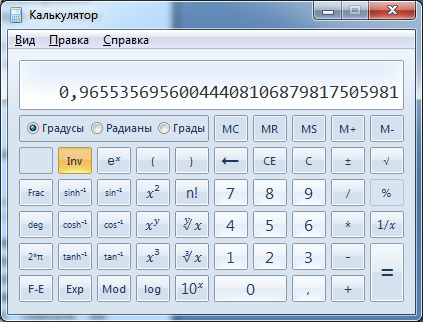 , арккосинус —
, арккосинус — 
 , арктангенс —
, арктангенс — 
 . Среди "отсутствующих" выделим арккотангенс.
. Среди "отсутствующих" выделим арккотангенс.
Обратные тригонометрические функции по определению возвращают величину угла, поэтому принципиально важным становится выбор нужной радиокнопки, устанавливающей интересующую единицу его измерения.
Пример 3 демонстрирует возможности "Калькулятора" по вычислению значений обратных тригонометрических функций.
Задача 3. Вычислить arcsin ½,arccos 1/2 , arctg 1 (в градусной и радианной мере)
Задача 4. sin(arcsin 0,7), cos(arcsin 0,6), sin(arccos 0,8), arctg (tg π3), sin arctg √2.
Если результат вычисления обратной тригонометрической функции получен в градусах, то возможно представить его не десятичной дробью, но выражением, содержащим градусы, минуты и секунды. Подобное преобразование осуществляется благодаря нажатию кнопки  .
.
Полученное представление обладает небольшим недостатком, ведь в нём отделёнными друг от друга будут лишь градусы и минуты. Минуты никак не отделяются от секунд, а секунды — от своих долей (десятых, сотых и т. д.). Потому это представление необходимо уметь правильно читать. Ниже покажем основные правила чтения результата, выраженного в формате "Градусы–Минуты–Секунды".
Информация о градусах предоставлена левее запятой.
Минуты представляются числом, состоящим из одной или двух цифр, расположенных сразу после запятой. Если после запятой имеется одна цифра, она показывает количество десятков минут.
Число секунд показано одной или двумя цифрами, расположенными сразу после цифр числа минут. Если количество секунд выражено одной цифрой (т. е. после запятой имеется всего три цифры), она показывает количество десятков секунд.
Цифры, начиная с пятой правее запятой и далее (если они есть), показывают десятичные доли секунды.
В Примере 5 приведены расчёты, в ходе которых в текстовое поле "Калькулятора" выводятся, кроме градусов, минуты и секунды, производится оценка их результатов.
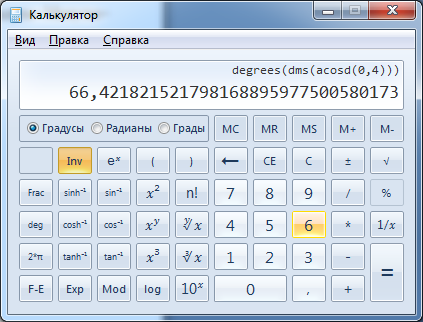
Задача 5. Показать значение угла, выраженное в градусах, минутах и секундах, если его косинус равен 0,4.
Решение. Если cos α = 0.4, то, чтобы определить угол, достаточно вычислить α = arccos 0.4.
Произведём расчёт:
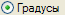



 .
. 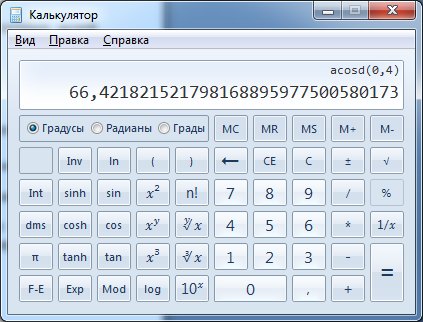
Осталось преобразовать это значение так, чтобы вместо десятичных долей градуса были видны минуты и секунды:

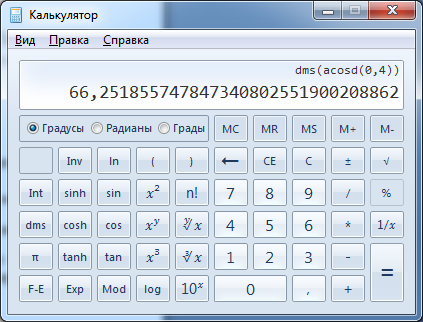 .
.
Мы видим, что искомый угол приближённо равен α ≈ 66° 25ʹ 18ʺ.
Сочетание 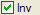
 позволяет преобразовать представление "Градусы–Минуты–Секунды" в обычное десятичное.
позволяет преобразовать представление "Градусы–Минуты–Секунды" в обычное десятичное.
Задание 4. Подготовка ответов на контрольные вопросы по теме «Основы тригонометрии»
Какие величины принимаются за единицу при градусном и радианном измерении дуг (углов).
Какие формулы используются для перехода от градусного изменения к радианному и от радианного к градусному.
Чему равна градусная мера дуги в 1 рад?
Чему равна радианная мера дуги в 10?
По какой формуле вычисляется длина дуги, измеренная в радианах?
По какой формуле вычисляется площадь сектора, центральный угол которого измерен в радианах?
Дайте определение единичной окружности. Как записывается уравнение единичной окружности?
Какие дуги в единичной окружности называются положительными (отрицательными)?
В чем заключается соответствие между точками числовой оси и точками числовой единичной окружности, имеющими общие нулевые точки?
Дайте определения тригонометрических функций числового аргумента и укажите области их определения.
Как определяются знаки тригонометрических функций по четвертям?
Какие тригонометрические функции являются четными и какие – нечетными?
Дайте определение периодической функции.
Являются ли числа, кратные наименьшему периоду, периодам функции?
Какие числа являются периодами функций синуса и косинуса?
Какие числа являются периодами функций тангенса и котангенса?
Какие формулы называются формулами приведения?
Сформулируйте правила составлений формул приведения
Какие тригонометрические уравнения называются простейшими?
Что понимается под решением тригонометрического уравнения?
Перечислите основные способы решения тригонометрических уравнений.