Типовые задачи по формированию универсальных учебных действий
на уроках математики (8-9 класс)
Важнейшей задачей современной системы образования является формирование универсальных учебных действий (УУД), обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию. В статье идет речь о том, как научить учащегося самостоятельно осуществлять деятельность учения, ставить учебные цели, искать и использовать необходимые средства.
Требования к предметным результатам освоения базового курса математики должны отражать:
1) сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
2) сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
3) владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
4) владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
5) сформированность представлений об основных понятиях, идеях и методах математического анализа;
6) владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
7) сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
8) владение навыками использования готовых компьютерных программ при решении задач.
Требования к предметным результатам освоения углубленного курса математики должны включать требования к результатам освоения базового курса и дополнительно отражать:
1) сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;
2) сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
3) сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;
4) сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
5) владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.
Регулятивные учебные действия обеспечивают возможность управления познавательной и учебной деятельностью посредством постановки целей, планирования, контроля, коррекции своих действий, оценки успешности усвоения.
Можно подобрать задания следующего типа:
• «Преднамеренные ошибки».
• «Ищу ошибку».
• Поиск информации в предложенных источниках.
• Взаимоконтроль.
• Диспут.
• Контрольный опрос на определенную проблему.
Задание № 1: «Ищу ошибки».
Цель: ученик самостоятельно учится определять цель своей деятельности, планировать её самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат.
Форма выполнения задания: индивидуальная работа с последующей проверкой и коллективным обсуждением.
Описание задания: В задании надо найти ошибку в решении, объяснить на какое правило она допущена, предложить правильное решение
1)
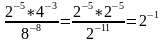
Решение. Показаны достаточно распространённые ошибки неверных действий со степенями.
2) Почему так получилось?
Докажем, что 5 = 1.
От обеих частей этого равенства отнимем по 3, результаты возведем в квадрат
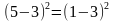 . Получим: 4 = 4.
. Получим: 4 = 4.
Это равенство верное. Значит, и исходное также верное, то есть 5 = 1.
Задание № 2.
Цель: формирование положительного отношения к процессу познания, мотивация учения, развитие интереса к математике, выработка навыков контроля и самоконтроля.
Форма выполнения задания: работа индивидуальная с последующей взаимопроверкой.
Описание задания: учащиеся подготовили домашнее задание по геометрии после прохождения темы «Подобие треугольников» № 570, 571 Л. С.Атанасян Геометрия 7 – 9 кл.
№570. Диагональ АС параллелограмма ABCD равна 18 см. Середина М стороны АВ соединена с вершиной D.Найти отрезки, на которые диагональ АС делится отрезком MD.
№571. В треугольнике 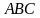 медианы
медианы 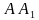 и
и 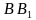 пересекаются в точке
пересекаются в точке  . Найти площадь треугольника
. Найти площадь треугольника 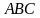 , если площадь треугольника
, если площадь треугольника 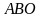 равна
равна  .
.
На уроке дается задание (самостоятельная работа):
найти площадь треугольника, если одна из его сторон равна 20 см, а медианы, проведенные к двум другим сторонам, равны 18 см и 24 см.
Однозначно предполагается, что домашнее задание будет выполнено, иначе на уроке не удастся решить самостоятельную работу. Ученик должен найти необходимые данные в домашней работе и применить их для решения задачи.
Вырабатывается навык применения известных планиметрических формул.
Коммуникативные учебные действия обеспечивают возможности сотрудничества: умение слышать, слушать и понимать партнера, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга, уметь договариваться, вести дискуссию, правильно выражать свои мысли, оказывать поддержку друг другу и эффективно сотрудничать как с учителем, так и со сверстниками.
Можно подобрать задания следующего типа:
Составь задание партнеру
Отзыв на работу товарища
Групповая работа по составлению кроссвордов
«Подготовь рассказ на тему…»
«Объясни …»
Задание № 1: Работа с консультантами.
Цель: формирование коммуникативных действий, направленных на структурирование информации по данной теме, умение сотрудничать в процессе создания общего продукта совместной деятельности.
Форма выполнения задания: работа индивидуальная коллективная с последующей взаимопроверкой и коллективным обсуждением.
Описание задания: при закреплении какой-либо темы можно учащимся даю задания. Назначаются консультанты, к которым можно обратиться за помощью, разрешается задать им только один вопрос. Затем консультанты проверяют выполненные задания и оценивают их.
Задание № 2: «Составь задание партнеру»
Цель: формирование коммуникативных действий, направленных на умение сотрудничать в процессе обучения(закрепления материала).
Форма выполнения задания: работа в парах
Описание задания: 1) придумать задачи на вычисление площадей плоских фигур. Сильные учащиеся составляют задачи по данной теме и предлагают решить их своим товарищам. Проверяется теоретический материал и вырабатываются навыки решения задач по заданной теме, правильное применение формул. Такую работу хорошо проводить в классах базового уровня подготовки.
2) во время проверки домашнего задания после ответа учащегося прошу остальных детей задать ему 2-3 вопроса по изучаемой теме. Это актуализирует работу класса . Подводится итог «Самый интересный вопрос».
Познавательные учебные действия включают действия исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания.
Можно подобрать задания следующего типа:
«Найти отличия»,
«Поиск лишнего»,
«Лабиринты»,
«Цепочки»,
Составления схем-опор,
Работа с разными видами таблиц,
Составления и распознавание диаграмм.
Задание № 1: «Диаграммы»
Цель:формирование личностных качеств, гражданской идентичности учащихся.
Форма выполнения задания: работа в парах.
Описание задания: учащиеся знакомятся с диаграммой, выясняют, какие данные в себя включает, отвечают на вопросы учителя, составляют свои вопросы к диаграмме, выбирают варианты верных (неверных) ответов из предложенных и др.
На рисунке точками изображено число родившихся мальчиков и девочек за каждый календарный месяц 2013 года в городском роддоме. По горизонтали указываются месяцы, по вертикали — количество родившихся мальчиков и девочек (по отдельности). Для наглядности точки соединены линиями.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику рождаемости в этот период.
Таблица
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ РОЖДАЕМОСТИ |
| А) 1-й квартал года Б) 2-й квартал года В) 3-й квартал года Г) 4-й квартал года | 1) Рождаемость мальчиков в течение 2-го и 3-го месяцев периода была одинаковой. 2) Рождаемость девочек снижалась в течение всего периода. 3) В каждом месяце периода девочек рождалось больше, чем мальчиков. 4) В каждом месяце периода мальчиков рождалось больше, чем девочек. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Задание № 2: «Угадай фразу»
Цель: развивать умение составлять план действий, последовательно выполнять математические операции.
Форма выполнения задания: индивидуальная работа
Описание задания:
Проводится в виде игры. Класс делится на две группы. Задания написаны на доске. Учащиеся (из каждой группы по одному) выходят по очереди. Результат решения соответствует какой-либо букве. Буквы лежат на отдельном столе. Ученик находит полученную букву, на обратной стороне которой написан её порядковый номер в фразе. Фраза записывается на доске. Выигрывает та группа, которая быстрее это сделает.
Ключ к расшифровке высказывания.
| Уравнение | Ответ | Буква | № окошка |
| 
| – 2,5; 1 | А | 15 |
| 
| - 2;  | Б | 25 |
| 
|  ; 1 ; 1
| В | 1,12,16 |
| 
| - 0,5; 0 | Г | 18 |
| 
| - 1; 0 | Е | 2,7,9,13,17 |
| 
| ±2 | И | 4,6,30,35 |
| 
|  ; 0 ; 0
| К | 14 |
| 
| ± | Л | 3,10,34 |
| 
| -2,5; 0 | М | 31 |
| 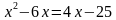
| 5 | Н | 26 |
| 
| -2,5 | О | 11,19,12,24,27 |
| 
| 
| П | 21 |
| 
| ±1 | Т | 29,36 |
| 
| ±1;  | С | 20,23,28,33 |
| 
| 
| Ч | 5,8 |
| | -1,25; 2 | Ы | 32 |
| | 1; 4 | Ь | 37 |
Величие человека – в его способности мыслить. Блез Паскаль (1623-1662)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | 16 | | 17 | 18 | 19 |
| | | | | | | | | | | | | | | | | | | | | | |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | | 31 | 32 | 33 | 34 | 35 | 36 | 37 | | | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Личностные учебные действия позволяют сделать учение осмысленным, увязывая его с реальными жизненными целями и ситуациями. Личностные действия направлены на осознание, исследование и принятие жизненных ценностей, позволяют сориентироваться в нравственных нормах и правилах, выработать свою жизненную позицию в отношении мира.
Можно предложить задания типа:
участие в проектах;
подведение итогов урока;
творческие задания, имеющие практическое применение;
самооценка событий.
Задание № 1:«Решение задач на сложные проценты» (урок-семинар)
Цель: Защита своих мини-проектов «Вычисления процентов в жизненных ситуациях». Учащиеся слушают, обсуждают, оценивают, выбирают лучшую работу для школьной конференции. Демонстрируют умения представлять конкретное содержание и сообщать его в письменной и устной форме, адекватно использовать речевые средства для дискуссии и аргументации своей позиции.
Форма выполнения задания: индивидуальная (или в парах)
Описание задания:
В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Задание № 2:«Решение текстовых задач».
Цель:При выполнении данного задания ученикам придется вспомнить знания, полученные ранее при решении задач на движение по воде, умения переводить в единые единицы измерения, знания, полученные на уроках физики, обсудить различные способы решения данной задачи.
Форма выполнения задания: индивидуальная.
Описание задания:
Из города А в город В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.







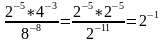
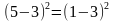 . Получим: 4 = 4.
. Получим: 4 = 4.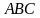 медианы
медианы 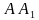 и
и 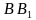 пересекаются в точке
пересекаются в точке  . Найти площадь треугольника
. Найти площадь треугольника 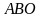 равна
равна  .
.




 ; 1
; 1



 ; 0
; 0