Интеграция алгебраических и геометрических
методов в решении задач
Понятие « интеграция» ( лат. Intequatio – восстановление, восполнение, объединение в целое каких- нибудь частей, элементов; как состояние связанности в целое отдельных диффиренцированных частей, а также как процесс, ведущий к такому состоянию.
Алгебраический метод - метод, заключающийся в употреблении букв и буквенных выражений, над которыми по определенным правилам производятся преобразования. Его называют еще методом буквенных вычислений.
Геометрический метод характеризуют как метод, идущий от наглядных представлений. Признаками этого метода являются геометрические представления и законы геометрии, в которых отражены свойства геометрических фигур.
Алгебраические : метод тождественных преобразований; метод уравнений и неравенств; функциональный метод; векторный метод; координатный метод.
Геометрические: метод длин; метод треугольников; метод параллельных прямых; метод соотношений между сторонами и углами треугольника; метод четырехугольников; метод площадей ; метод подобия треугольников, тригонометрический метод, основанный на соотношениях между сторонами и углами треугольника, выраженными через тригонометрические функции; метод геометрических преобразований; графический метод.
Каждый метод состоит из определенных приемов , а каждый прием - из действий. Под интеграцией алгебраического и геометрического методов будем понимать процесс сочетания данных методов или связи их приемов в один метод.
Примеры .
Формулы сокращенного умножения, « квадрат двучлена»
Алгебраический метод
( a b )2 = a2 2 ab + b2.
( a + b )2 = ( a + b )( a + b ) = a2 + ab+ ab + b2 = a2 + 2 ab + b2.
Г
b
a еометрическая иллюстрация
Д
а

b
ано:




b




a + b
a b-a
b a


Задача 2.
В одном элеваторе было зерна в два раза больше, чем в другом. Из первого элеватора вывезли 750 т зерна, а на второй элеватор привезли 350 т, после чего в обоих элеваторах зерна стало поровну. Сколько зерна было первоначально в каждом элеваторе ?
Решение. Алгебраический метод
х т – зерна было первоначально во втором элеваторе,
2х т- зерна было первоначально в первом элеваторе;
( 2х – 750 ) т – осталось в первом элеваторе;
( х + 350 ) т – стало во втором элеваторе.
По условию задачи в обоих элеваторах зерна стало поровну.
Уравнение : 2х – 750 = х + 350;
х = 1100; 2х = 2200.
Ответ: 2200 т зерна было первоначально в первом элеваторе, 1100 т - во втором.
Геометрический метод. Решаем задачу с помощью линейной диаграммы.
Построенная линейная диаграмма превращает алгебраическую задачу в геометрическую, решение которой основано на использовании свойств длины отрезка:
а) равные отрезки имеют равные длины; больший отрезок имеет большую длину;
б) если точка лежит на отрезке, то длина всего отрезка равна сумме длин получившихся отрезков.
Решение. Отрезок АВ изображает количество зерна в первом элеваторе первоначально;
Отрезок МР - количество зерна во втором элеваторе, причем 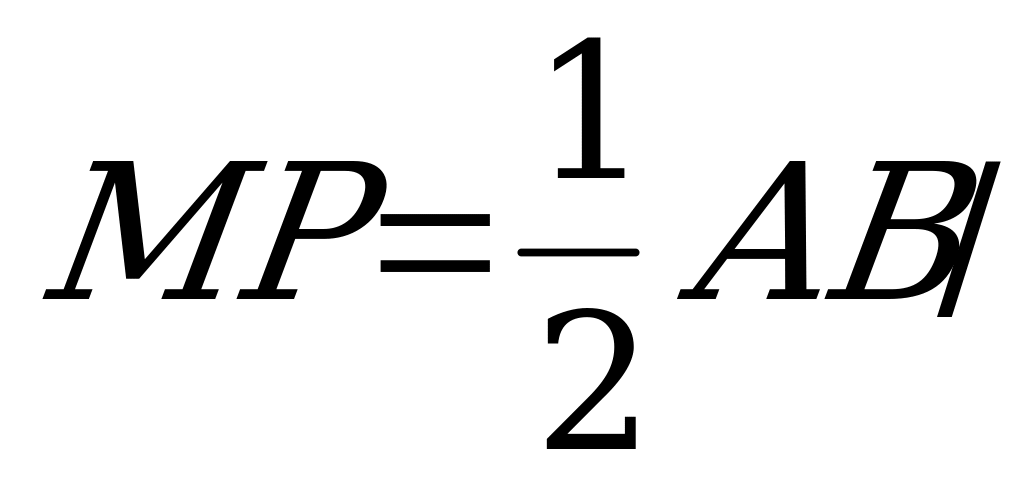
а) Диаграмма:
1
350 750
элеватор
 А О В
А О В
С
2 М Р К элеватор
М Р К элеватор
АС = МК ; ОС = 350; РК = 350; ВС = 750.
б) МР = АО = ОВ ( по построению ); ОВ = ОС + ВС = 350 + 750 = 1100;
значит МР = ОВ = 1100; АВ = 1100 2 = 2200.
Ответ: 2200 т зерна в первом элеваторе; 1100 т зерна во втором элеваторе было первоначально.
Линейная диаграмма позволила « усмотреть» ответ задачи прямо по чертежу.
Задача 3.
На одном садовом участке в пять раз больше кустов малины, чем на другом. После того, как с первого участка пересадили на второй 22 куста, то на обоих участках кустов малины стало поровну. Сколько кустов малины было на каждом участке ?
Решение. Алгебраический метод.
Пусть х кустов малины на втором участке, 5х кустов – на первом.
( 5х – 22 ) кустов – осталось на первом участке;
( х + 22 ) кустов -- стало на втором участке.
По условию задачи кустов малины на обоих участках стало поровну.
Уравнение: 5х – 22 = х + 22; х = 11; 5х = 55.
Геометрический метод.
Пусть отрезок АВ – количество кустов малины на первом участке, а
отрезок CD – количество кустов малины на втором участке,
причем AB = 5CD ( по условию).
BF = DK = 22.
1 A F B участок
A F B участок
2
С D K
участок 
CD = 1 часть; АВ = 5 частей; AF = CK = ( 5 + 1 ) 2 = 3 части, значит BF = 2 части.
BF = 2 CD = 22, значит CD = 11; АВ = 11 5 = 55.
Ответ: 55 кустов малины было на первом участке, 11 кустов -- на втором.
С помощью линейных диаграмм решаются задачи, в которых даны отношения значений величин ( « на»; « в»; меньше; больше) и рассматривается одна или несколько ситуаций.
Текстовые задачи, в которых одна из величин представляет собой произведение двух других, позволяет интегрировать метод площадей, основанный на свойствах площади, и метод уравнений и неравенств.
Задача 4.
Бригада лесорубов ежедневно перевыполняла норму на 16 м3, поэтому недельную ( шесть рабочих дней) она выполнила за четыре дня. Сколько кубометров леса заготовляла бригада в день?
Решение. Алгебраический метод.
Пусть х м3 – дневная производительность бригады по плану,
( х + 16 ) м3 – фактическая производительность бригады в день,
6 х м3 – недельная норма бригады,
4 ( х + 16 ) м3 – фактическая работа.
По условию задачи работа была выполнена одинаковая.
Уравнение: 6х = 4 ( х + 16 ); х = 32.
32 м3 – дневная норма бригады по плану, 32 + 16 = 48 ( м3 ) – заготовляла бригада в день фактически.
Ответ : 48 м3.
Геометрический метод.
В задаче рассматривается произведение двух величин А = р п, где А – выполненная работа, р – производительность, п – количество дней. Для наглядности представим его в виде прямоугольников, стороны которых изображают численные значения величин р и п, а площадь прямоугольника изображает их произведение S = A.
Решение задачи проходит в три этапа:
построение двумерной диаграммы, т.е. перевод задачи на язык площадей;
решение получившейся геометрической задачи путем составления уравнения на основе использования свойств площади многоугольника;
перевод полученного ответа с геометрического языка на естественный.
1 – й этап. Анализ условия задачи. Вопросы:
а) Чему равна работа ? Как же можно изобразить на рисунке ее, в виде какой фигуры ?
б) Что будут представлять собой стороны прямоугольника ?
в) Сколько прямоугольников надо изобразить ?
г) Что можно сказать о площадях этих прямоугольников ? ( Они равны )
( Например: 6 8 = 4 12 = 48)



S1
S2 S3
D
E N
A
2
K
B
16
C M
АВ – обозначает количество дней недели; ВС – дневная производительность по плану;
SABCD = AB BC – недельная норма бригады;
ВК – количество фактически отработанных дней; ВМ – фактическая дневная производительность бригады;
SBKNM = BK BM – фактически выполненная работа.
2 – й этап. Рассматриваются площади получившихся прямоугольников и устанавливается соотношения между ними.
Вопрос: Назовите прямоугольники с равными площадями ?
SABCD = SBKNM ; S1 + S2 = S2 + S3 ; то S1 = S3.
S1 = 2 KE ; S3 = 16 4 = 64 ; 2 KE = 64; KE = 32.
ВС = КЕ = 32; ВМ = ВС + СМ = 32 + 16 = 48.
3 –й этап. 48 м3 – фактическая производительность бригады.
Ответ: 48 м3 леса бригада заготовляла в день.
Задача 5.
На рисунке AB = AC; AP = PQ = QR = R B = BC. Найдите угол А.

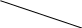
А
С В Q R
1 = A = x 0 ;
2 = 2x 0 ( Внешний угол APQ );
4 = 2 = 2 x0.
3 = 1800 – ( 2 + 4 ) = 1800 – 4 x0 ;
5 = 1800 – ( 1 + 3 ) = 3 x0;
6 = 5 = 3x0 ; 7 = B - 6.
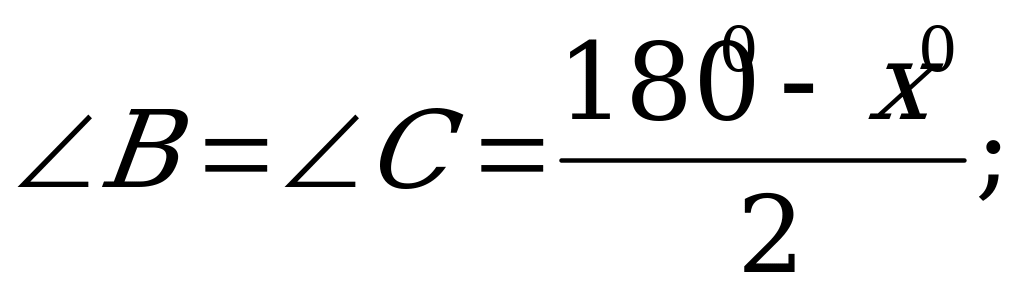
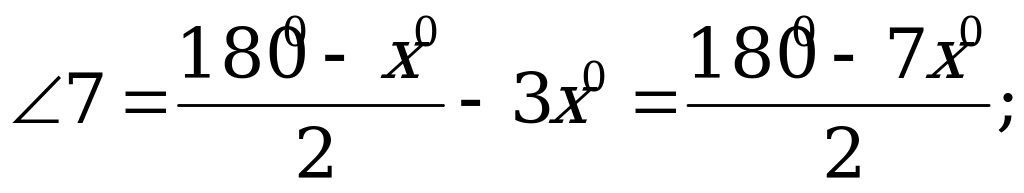
Так как 8 = С , то
С + 8 + 7 = 2 С + 7 = 1800,
или 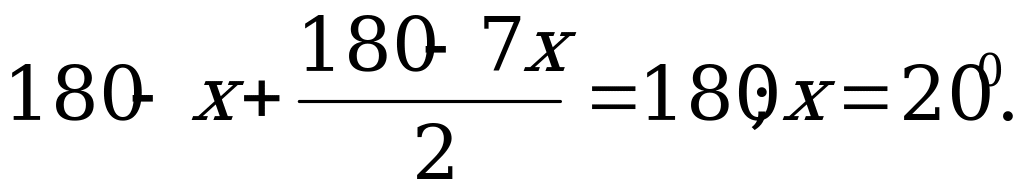
Ответ : А = 200.
Решение. Пусть
А = х 0.
Р

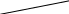
При решении этой задачи использовались метод треугольников и метод уравнений.
Задача 6.
Чтобы ликвидировать опоздание на 1 час поезд на перегоне в 720 км увеличил скорость, с которой должен был идти по расписанию, на 10 км/ч. Какова скорость движения поезда по расписанию?
Решение.
Алгебраический метод.
Пусть х км/ч – скорость по расписанию;
( х + 10 ) км/ч – скорость на перегоне в 720 км;
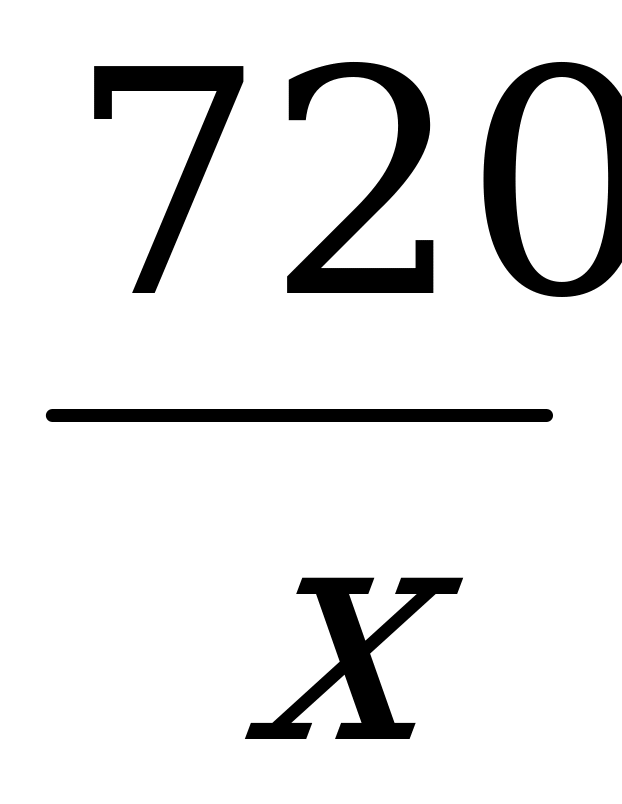 часов – время по расписанию;
часов – время по расписанию; 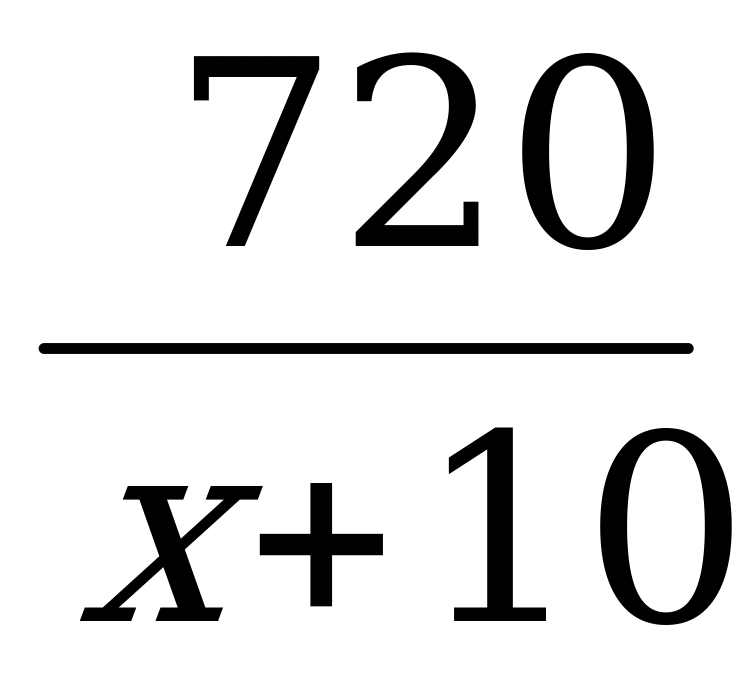 часов – фактическое время на перегоне.
часов – фактическое время на перегоне.
По условию задачи поезд опаздывал на 1 час.
Уравнение: 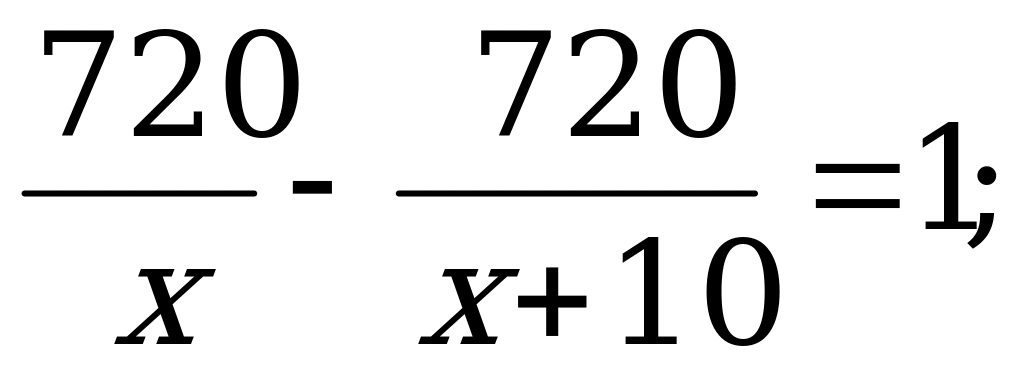 ( * ). По смыслу задачи х 0.
( * ). По смыслу задачи х 0.
После преобразований уравнение ( * ) принимает вид : х2 + 10х – 7200 = 0.
Корнями уравнения являются: х1 = 80; х2 = - 90 , по смыслу задачи не подходит.
Ответ : 80 км/ч – скорость поезда по расписанию.
Геометрический метод
В задаче рассматривается равномерное движение, то путь, пройденный телом, равен произведению скорости движения на время движения, поэтому для решения задачи можно использовать двумерную диаграмму.
1

 D C
D C
K
A
M F
x B 10 E
S3
S2
S1
1
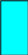
Пусть АВ= х км/ч – скорость поезда по расписанию
AD -- время по расписанию
SABCD = AB AD = 720 ( км )
АЕ = ( х + 10 ) км/ч – фактическая скорость
АК – фактическое время движения
SАКFE = AE AK = 720 ( км )
– й этап. Анализ текста задачи. Построение двумерной диаграммы.
2 – й этап. S1 + S3 = S2 + S3 , то S1 = S2
S1 = x 1 = x ; S2 = 10 EF;
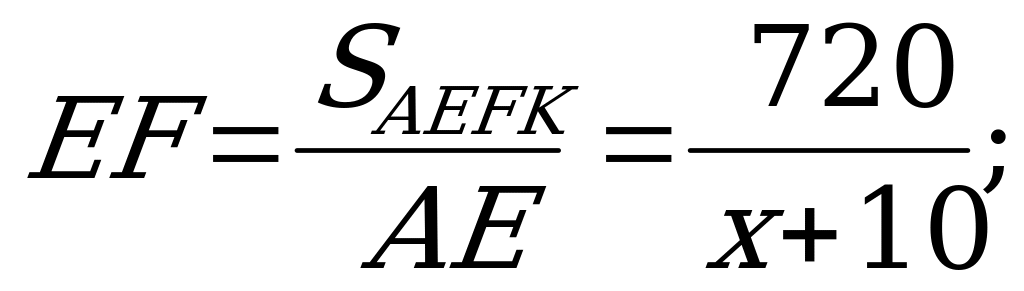
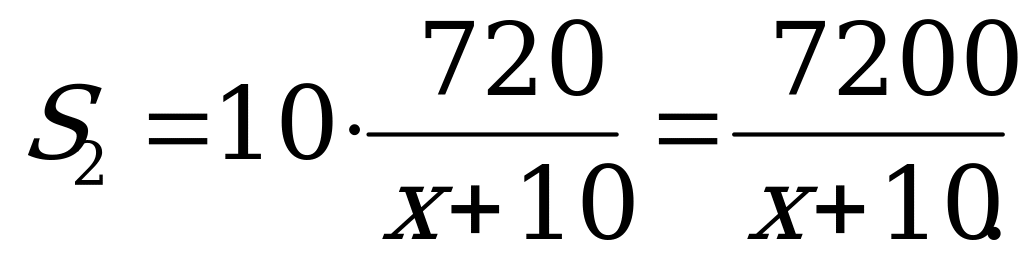
Так как S2 = S1, получаем уравнение 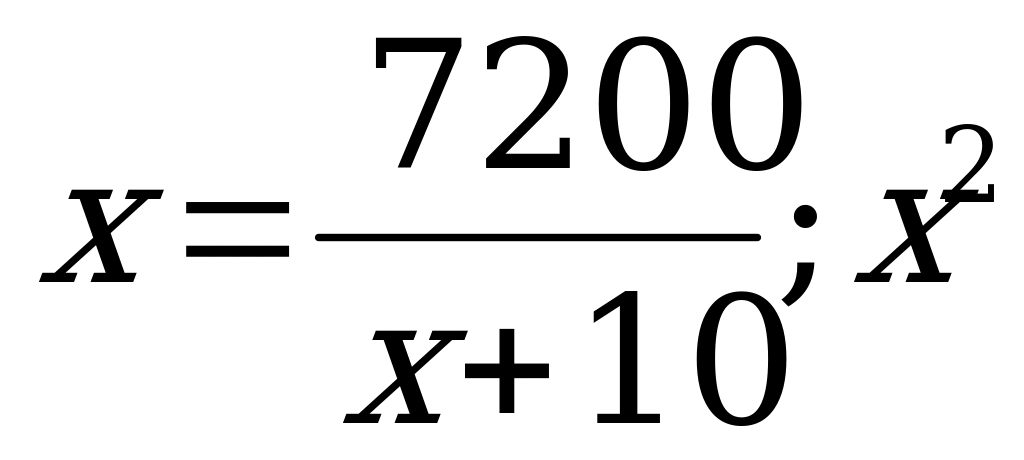 + 10 х – 7200 = 0.
+ 10 х – 7200 = 0.
Далее аналогично алгебраическому методу, решаем уравнение.
Ответ: 80 км/ч.
Примеры геометрических задач, в решении которых используется метод площадей и метод уравнений и неравенств.
Задача 7.
Средняя линия трапеции равна 10 см и делит ее на две такие трапеции, что
S1 : S2 = 3 : 5. Найдите большее основание трапеции.


О
Sx
M 10 S1 N
A b S2 D
Решение. Продолжим боковые стороны трапеции до пересечения в
точке О.
Площади получившихся трапеций выражаются формулами:
B a \C
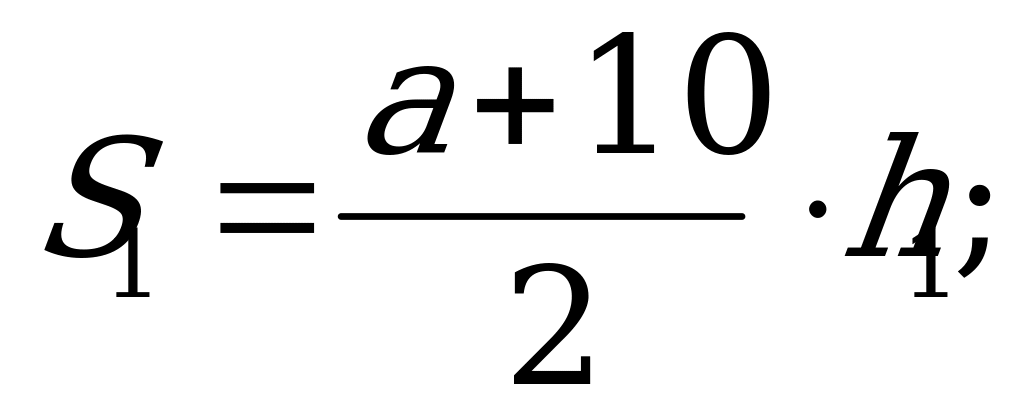

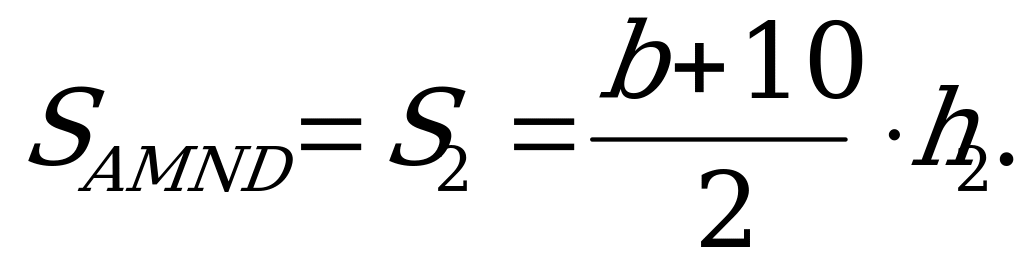
h1 = h2 = h; S1 : S2 = 3 : 5 получаем систему уравнений:
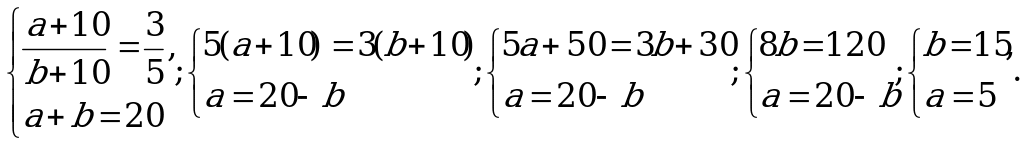 Ответ : 15 см.
Ответ : 15 см.
Задача 8.
В А
А
c
остроугольном треугольнике
АВС со сторонами
BC = a; AC = b; AB = c проведена высота
АН. В каком отношении точка
Н делит сторону
ВС ?

b

С Н а В
Решение. 1) Выразим высоту АН из прямоугольных треугольников АСН и АВН:
АН2 = АС 2 – СН 2 = b2 – ( a – BH )2 ; АН2 = АВ 2 – ВН 2 = c 2 – BH 2.
2) Приравняем эти значения АН 2 , получим уравнение:
b 2 – ( a - BH )2 = c 2 – BH 2; b 2 – a 2 + 2a BH – BH 2 = c 2 – BH 2;
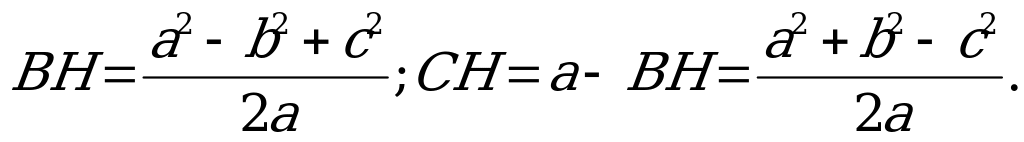
Значит 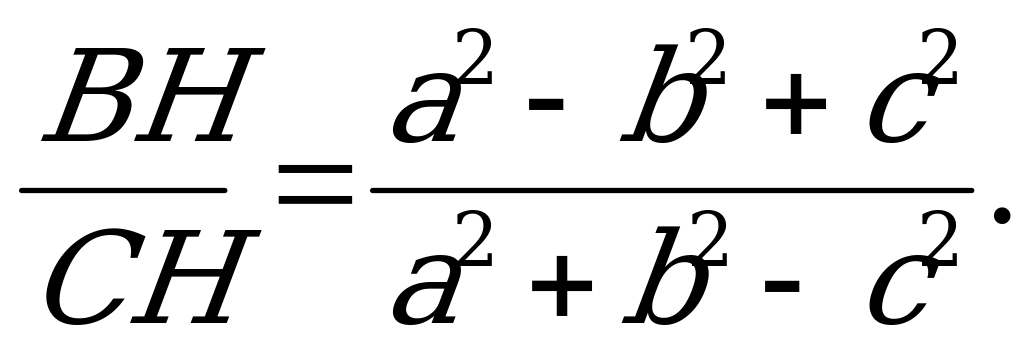
Ответ : 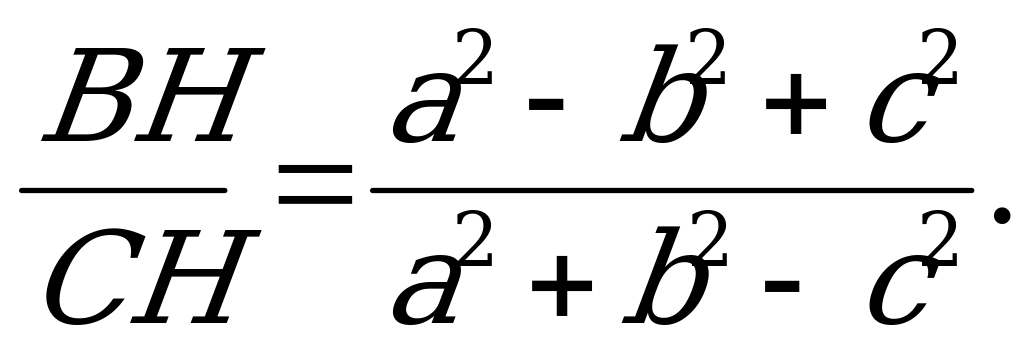















 А О В
А О В  М Р К элеватор
М Р К элеватор  A F B участок
A F B участок 







 D C
D C 


 А
А 










