Просмотр содержимого документа
«Линейная алгебра (матрицы)»
II тема: «Линейная алгебра. Матрица».
1 вариант
1. Вычислить определитель:  .
.
A) – 2 B) 0 C) 20 D) 2 E) – 18
2. Найти матрицу С = – А, если: 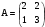 .
.
A) 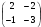 B)
B) 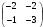 C)
C) 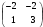 D)
D) 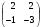 E)
E) 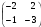
3. Решить систему уравнений по правилу Крамера: 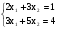 .
.
A) 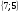 B)
B) 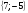 C)
C) 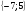 D)
D) 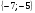 E)
E) 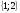
4. Найти матрицу С = А · В, если: 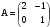 и
и 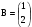 .
.
A) 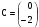 B)
B) 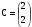 C)
C) 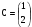 D)
D) 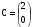 E)
E) 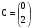
5. Найти матрицу С = А + Е, если: 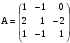 .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
II тема: «Линейная алгебра. Матрица».
2 вариант
1. Вычислить определитель:  .
.
A) – 2 B) 2 C) 0 D) 4 E) – 6
2. Найти матрицу С = 0,5 А, если:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
3. Решить систему уравнений по правилу Крамера:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
4. Найти матрицу С = А · В, если:  и
и  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
5. Найти матрицу С = А + В, если:  и
и  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
II тема: «Линейная алгебра. Матрица».
3 вариант
1. Вычислить определитель:  .
.
A) 10 B) – 15 C) 1 D) 0 E) – 1
2. Найти матрицу С =  А, если:
А, если:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
3. Решить систему уравнений по правилу Крамера:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
4. Найти матрицу С = А · В, если:  и
и  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
5. Найти матрицу С = А + В, если:  и
и  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
II тема: «Линейная алгебра. Матрица».
4 вариант
1. Вычислить определитель:  .
.
A) 2 B) – 1 C)  D)
D)  E) 1
E) 1
2. Найти матрицу С = – 2А, если:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
3. Решить систему уравнений по правилу Крамера:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
4. Найти матрицу С = А · В, если:  и
и  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
5. Найти матрицу С = А – В, если:  и
и  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
II тема: «Линейная алгебра. Матрица».
5 вариант
1. Вычислить определитель: .
A) 1 B)  C)
C)  D)
D)  E)
E) 
2. Найти матрицу С = 2А, если:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
3. Решить систему уравнений по правилу Крамера:  .
.
A)  B)
B)  C)
C)  D)
D)  E)
E) 
4. Найти матрицу С = А · В, если:  и
и  .
.
A)  B)
B) 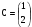 C)
C)  D)
D)  E)
E) 
5. Найти матрицу С = А + В, если:  и
и  .
.
A) B)  C)
C)  D)
D)  E)
E) 







 .
. 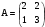 .
.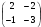 B)
B) 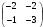 C)
C) 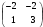 D)
D) 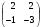 E)
E) 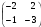
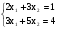 .
.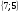 B)
B) 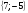 C)
C) 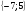 D)
D) 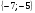 E)
E) 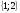
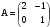 и
и 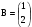 .
.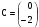 B)
B) 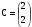 C)
C) 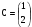 D)
D) 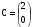 E)
E) 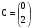
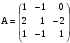 .
. B)
B)  C)
C)  D)
D)  E)
E) 









