7 класс.
ГЛАВА 2. Функции.
§ 6. Линейная функция.
Количество функций неограничено. Однако, существуют функции, которые можно объединить в группы. Они имеют общую формулу, схожие свойства, графиком таких функций является одна и та же кривая. Прежде чем начать рассматривать одну из таких групп функций, введём несколько новых понятий.
Функция называется возрастающей, если большему значению х соответствует большее значение у (т.е. при увеличении х увеличивается у).
Функция называется убывающей, если большему значению х соответствует меньшее значение у (т.е. при увеличении х уменьшается у).
Рассмотрим это на графике.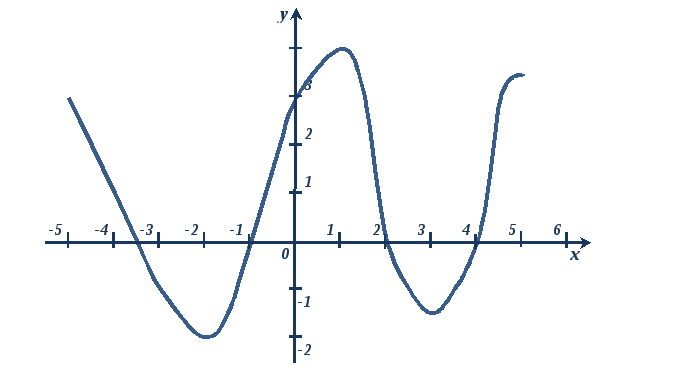
Фраза «при увеличении х…» означает, что мы рассматриваем график слева направо (также, как пишем и читаем). Если при этом график опускается вниз, то он убывает, если график поднимается вверх, то он возрастает.
На данном рисунке график убывает, если 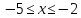 и
и 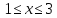 ; а возрастает, если
; а возрастает, если 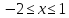 и
и 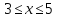 .
.
Это можно записать так:
функция убывает при 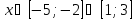 ;
;
функция возрастает при 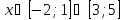 .
.
Теперь введём понятие линейной функции.
Линейной функцией называется функция, вида  , где
, где 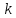 и
и 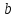 – некоторые числа.
– некоторые числа.
Например, 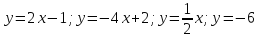 .
.
Графиком любой линейной функции является прямая.
В зависимости от значений 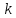 и
и 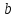 , линейная функция разделяется на три вида. Рассмотрим каждый из них.
, линейная функция разделяется на три вида. Рассмотрим каждый из них.
1. Если 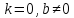 , то функция приобретает вид y = b. Такую функцию называют постоянной. Её графиком является прямая, параллельная оси Ox, проходящая через точку (0; b).
, то функция приобретает вид y = b. Такую функцию называют постоянной. Её графиком является прямая, параллельная оси Ox, проходящая через точку (0; b).
Область определения - 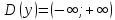
Область значений - 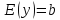
Функция является постоянной, поэтому промежутков возрастания и убывания у неё нет
Например, 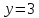 – постоянная функция, графиком является прямая, параллельная оси Ох, проходящая через точку
– постоянная функция, графиком является прямая, параллельная оси Ох, проходящая через точку 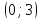 .
.
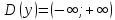
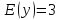
Промежутков возрастания и убывания нет.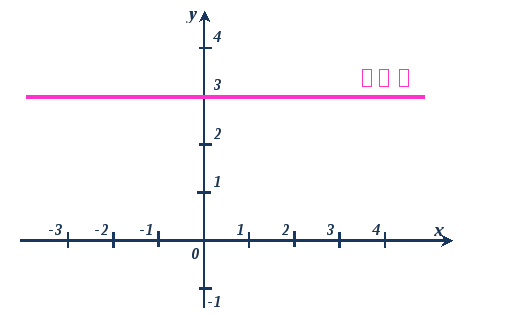
2. Если 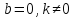 , то функция приобретает вид y = kx. Такую функцию называют прямой пропорциональностью. Её графиком является прямая, проходящая через начало координат и точку с произвольно выбранным значением аргумента
, то функция приобретает вид y = kx. Такую функцию называют прямой пропорциональностью. Её графиком является прямая, проходящая через начало координат и точку с произвольно выбранным значением аргумента 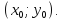 Если
Если 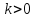 , то прямая составляет с положительным направлением оси Ox острый угол. Если
, то прямая составляет с положительным направлением оси Ox острый угол. Если 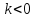 , то прямая составляет с положительным направлением оси Ox тупой угол. Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.
, то прямая составляет с положительным направлением оси Ox тупой угол. Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.
Область определения - 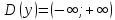
Область значений - 
Если 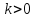 , то функция возрастает при
, то функция возрастает при 
Если 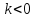 , то функция убывает при
, то функция убывает при  .
.
Например, а)  – прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку
– прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку  , и составляющая с положительным направлением оси Ох острый угол, т.к.
, и составляющая с положительным направлением оси Ох острый угол, т.к.  .
.
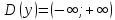

Функция возрастает при  .
.
б)  – прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку
– прямая пропорциональность, графиком является прямая, проходящая через начало координат и точку  , и составляющая с положительным направлением оси Ох тупой угол, т.к.
, и составляющая с положительным направлением оси Ох тупой угол, т.к.  .
.
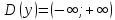

Функция убывает при  .
.
3. Если  , то функция не меняет свой вид
, то функция не меняет свой вид  . Это линейная функция. Её графиком является прямая, проходящая через точку
. Это линейная функция. Её графиком является прямая, проходящая через точку  и точку с произвольно выбранным значением аргумента
и точку с произвольно выбранным значением аргумента  . Коэффициент
. Коэффициент 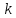 играет здесь такую же роль, как и в прямой пропорциональности.
играет здесь такую же роль, как и в прямой пропорциональности.
Область определения - 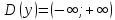
Область значений - 
Если 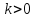 , то функция возрастает при
, то функция возрастает при 
Если 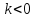 , то функция убывает при
, то функция убывает при  .
.
Например, а)  – линейная функция, графиком является прямая, проходящая через точки
– линейная функция, графиком является прямая, проходящая через точки  и
и  , и составляющая с положительным направлением оси Ох острый угол, т.к.
, и составляющая с положительным направлением оси Ох острый угол, т.к.  .
.
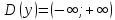

Функция возрастает при  .
.
б)  – линейная функция, графиком является прямая, проходящая через точки
– линейная функция, графиком является прямая, проходящая через точки 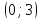 и
и  , и составляющая с положительным направлением оси Ох тупой угол, т.к.
, и составляющая с положительным направлением оси Ох тупой угол, т.к.  .
.
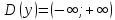

Функция убывает при  .
.
Рассмотрим теперь взаимное расположение графиков линейных функций.
Пусть даны две линейные функции  и
и  .
.
Если  , то графики данных функций совпадают.
, то графики данных функций совпадают.
Если  , то графики функций параллельны.
, то графики функций параллельны.
Если  , то графики функций пересекаются в точке
, то графики функций пересекаются в точке  (или в точке
(или в точке  , что то же самое).
, что то же самое).
Если  , то графики пересекаются. Для нахождения координат точки пересечения необходимо решить уравнение:
, то графики пересекаются. Для нахождения координат точки пересечения необходимо решить уравнение:  и найденное значение аргумента (х) подставить в любую из двух формул, посчитать полученное числовое выражение. Это и есть ордината точки пересечения графиков.
и найденное значение аргумента (х) подставить в любую из двух формул, посчитать полученное числовое выражение. Это и есть ордината точки пересечения графиков.
Например,
 и
и  . Так как у этих функций коэффициенты равны, то их графики параллельны.
. Так как у этих функций коэффициенты равны, то их графики параллельны.
 и
и  . Так как у этих функций коэффициенты k разные, а значения
. Так как у этих функций коэффициенты k разные, а значения 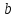 одинаковые и равны 1, то графики этих функций пересекаются в точке
одинаковые и равны 1, то графики этих функций пересекаются в точке  .
.
 и
и  . У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):
. У этих функций k и b имеют разные значения, поэтому, чтобы найти координаты точки пересечения графиков этих функций, решим уравнение (приравниваем правые части):



Подставляем найденное значение аргумента в любую из двух функций:

Значит, точка пересечения графиков данных функций  .
.
В завершение конкретизируем значение коэффициента k и числа b в формуле линейной функции:
коэффициент k показывает угол наклона прямой к положительному направлению оси Ох. Если 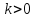 , этот угол острый; если
, этот угол острый; если 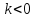 , то этот угол тупой;
, то этот угол тупой;
число b определяет точку пересечения прямой с осью Оу.  - точка пересечения.
- точка пересечения.
Из данных функций выбрать линейные:
Назовите коэффициенты k и b линейной функции  :
:
Для функции  представлена таблица:
представлена таблица:
Найдите коэффициент k и заполните таблицу.
Определите вид функции, постройте её график. Найдите область определения и область значений функции, найдите промежутки возрастания и убывания функции.
Не выполняя построения, определить угол наклона прямой к положительному направлению оси Ох и точку пересечения с осью Оу:
Функции заданы формулами  . Укажите те из них, графиком которых является прямая, проходящая через начало координат, и постройте эти графики.
. Укажите те из них, графиком которых является прямая, проходящая через начало координат, и постройте эти графики.
Функция задана формулой  . Определите:
. Определите:
значение функции, если значение аргумента равно  ;
;
значение аргумента, при котором значение функции равно  ;
;
возрастающей или убывающей является данная функция?
Постройте график функции  . Пользуясь графиком, найдите:
. Пользуясь графиком, найдите:
значение функции, если значение аргумента равно 
значение аргумента, при котором значение функции равно 
значения аргумента, при которых функция принимает положительные значения;
промежутки возрастания (или убывания) функции.
Не выполняя построения графика функции  , укажите, через какие точки проходит этот график: .
, укажите, через какие точки проходит этот график: .
Задайте формулой прямую пропорциональность, если известно, что её график проходит через точку  .
.
Постройте в одной системе координат графики функций и укажите координаты их точки пересечения:
 и
и  ;
;
 и
и  .
.
Не выполняя построения графиков функций  ;
;  , определите:
, определите:
чему равен угловой коэффициент каждой функции;
каково взаимное расположение графиков данных функций;
каковы координаты точек пересечения графиков функций с осями координат.
Не выполняя построения графиков функций  , определите:
, определите:
в какой точке каждый график пересекает ось у; ось х;
чему равен угловой коэффициент каждой функции;
каково взаимное расположение графиков данных функций.
Постройте в одной системе координат графики функций и запишите их область определения и область значений:  .
.
Не выполняя построения, найдите координаты точек пересечения с осями координат графиков функций:
Не выполняя построения графика функции  , найдите точку этого графика, у которой:
, найдите точку этого графика, у которой:
абсцисса равна ординате;
абсцисса и ордината – противоположные числа.
Найдите 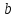 , если известно, что график функции
, если известно, что график функции  проходит через точку
проходит через точку  .
.
Найдите 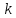 , если известно, что график функции
, если известно, что график функции  проходит через точку
проходит через точку  .
.
График функции  пересекает оси координат в точках
пересекает оси координат в точках  . Найдите значения
. Найдите значения 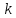 и
и 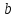 .
.
Все точки графика функции  имеют одинаковую ординату, равную
имеют одинаковую ординату, равную  . Найдите значения
. Найдите значения 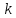 и
и 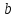 .
.
График функции  параллелен оси абсцисс и проходит через точку
параллелен оси абсцисс и проходит через точку  . Найдите значения
. Найдите значения 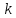 и
и 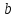 .
.
Постройте графики функций:
Не выполняя построения, найдите точки пересечения графиков функций:
 и
и 
 и
и  .
.
Задайте формулой линейную функцию, график которой изображён на рисунке.
Постройте график функции:
Пересекаются ли графики функций:
 и
и  ;
;
 и
и  ?
?
В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением.
Запишите формулу функции, график которой параллелен графику функции  и проходит через точку
и проходит через точку  .
.
Найдите координаты точки пересечения графиков функций
 и
и 
При каком значении параметра а графики функций  и
и
 параллельны? Постройте графики этих функций.
параллельны? Постройте графики этих функций.
При каком значении параметра а графики функций  и
и
 параллельны? Постройте графики этих функций.
параллельны? Постройте графики этих функций.
Постройте прямые, координаты точек которых удовлетворяют уравнению  .
.
Постройте прямые, координаты точек которых удовлетворяют уравнению  .
.
При каком значении k графики линейных функций  и
и  имеют более одной общей точки?
имеют более одной общей точки?
Найдите наибольшее и наименьшее значение линейной функции  на промежутке
на промежутке  .
.
4








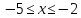 и
и 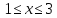 ; а возрастает, если
; а возрастает, если 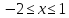 и
и 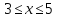 .
. 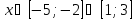 ;
;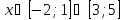 .
. , где
, где 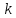 и
и 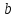 – некоторые числа.
– некоторые числа.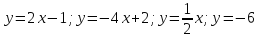 .
.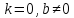 , то функция приобретает вид y = b. Такую функцию называют постоянной. Её графиком является прямая, параллельная оси Ox, проходящая через точку (0; b).
, то функция приобретает вид y = b. Такую функцию называют постоянной. Её графиком является прямая, параллельная оси Ox, проходящая через точку (0; b).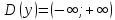
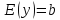
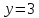 – постоянная функция, графиком является прямая, параллельная оси Ох, проходящая через точку
– постоянная функция, графиком является прямая, параллельная оси Ох, проходящая через точку 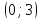 .
. 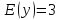

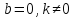 , то функция приобретает вид y = kx. Такую функцию называют прямой пропорциональностью. Её графиком является прямая, проходящая через начало координат и точку с произвольно выбранным значением аргумента
, то функция приобретает вид y = kx. Такую функцию называют прямой пропорциональностью. Её графиком является прямая, проходящая через начало координат и точку с произвольно выбранным значением аргумента 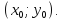 Если
Если 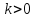 , то прямая составляет с положительным направлением оси Ox острый угол. Если
, то прямая составляет с положительным направлением оси Ox острый угол. Если 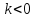 , то прямая составляет с положительным направлением оси Ox тупой угол. Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.
, то прямая составляет с положительным направлением оси Ox тупой угол. Поскольку от значения k зависит угол наклона прямой к положительному направлению оси Ох, то его называют угловым коэффициентом.









