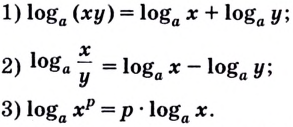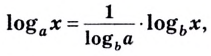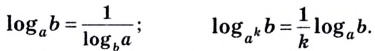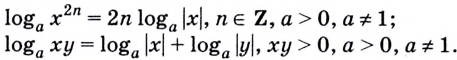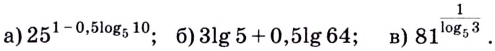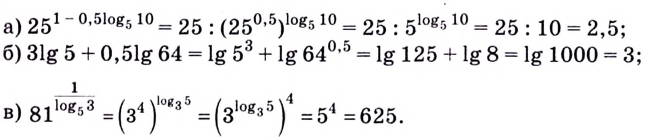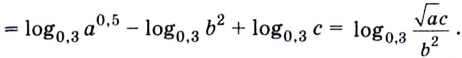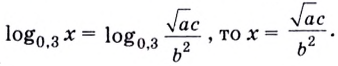Логарифм - формулы, свойства и примеры с решением
Множеством (областью) значений показательной функции 
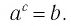
Такое значение аргумента единственное, так как если  и
и 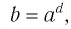 то по следствию из п. 2.3 верно равенство c = d. Это единственное значение аргумента с называют логарифмом числа b по основанию a и обозначают
то по следствию из п. 2.3 верно равенство c = d. Это единственное значение аргумента с называют логарифмом числа b по основанию a и обозначают 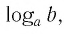 т. е.
т. е.
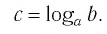
Таким образом, равенство 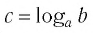 означает, что
означает, что 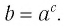 Сформулируем определение логарифма еще раз.
Сформулируем определение логарифма еще раз.
Определение:
Пусть 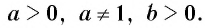 Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число b.
Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести число а, чтобы получить число b.
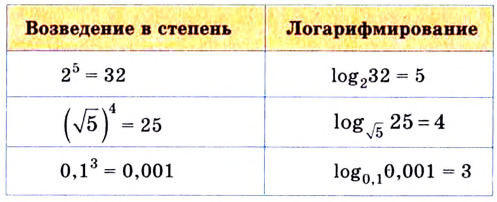
Приведем несколько примеров:
а)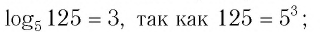
б) 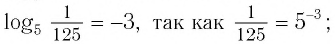
в)
г) 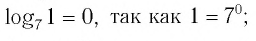
д) не имеет смысла, так как значение выражения
не имеет смысла, так как значение выражения 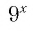 при любом значении х положительно и не может быть равно -9;
при любом значении х положительно и не может быть равно -9;
е) по определению логарифма не имеют смысла и такие выражения, как  поскольку основанием логарифма должно быть положительное число, отличное от единицы.
поскольку основанием логарифма должно быть положительное число, отличное от единицы.
Нахождение логарифма числа называется логарифмированием.
Обозначим 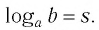 Тогда, согласно определению логарифма, верно равенство
Тогда, согласно определению логарифма, верно равенство  т. е.
т. е.

Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 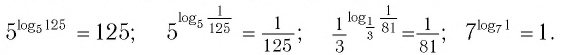 Основное логарифмическое тождество позволяет данное число b представить в виде степени с любым положительным основанием.
Основное логарифмическое тождество позволяет данное число b представить в виде степени с любым положительным основанием.
Например: 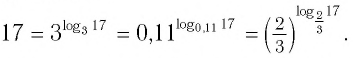
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 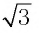 в виде логарифмов по основанию
в виде логарифмов по основанию 
б) Записать число -5 в виде логарифмов по основанию  и х
и х 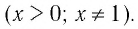
Решение:
а) По определению логарифма имеем:

б) По определению логарифма имеем:
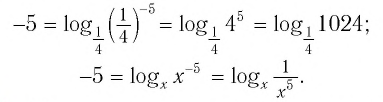
Пример:
Между какими целыми числами находится число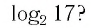
Решение:
Пусть 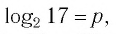 тогда верно равенство
тогда верно равенство  Поскольку
Поскольку 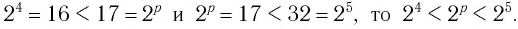 По свойствам показательной функции с основанием 2 имеем
По свойствам показательной функции с основанием 2 имеем 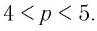 Значит,
Значит,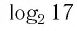 находится между числами 4 и 5.
находится между числами 4 и 5.
Ответ: 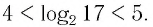
Пример:
Решить уравнение:
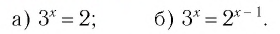
Решение:
а) Поскольку 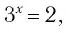 то по определению логарифма имеем
то по определению логарифма имеем 
б)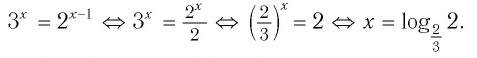
Ответ: 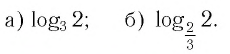
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 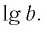 . Таким образом,
. Таким образом, 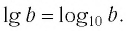
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
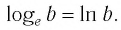
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
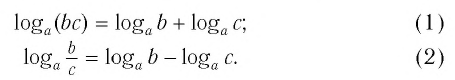
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
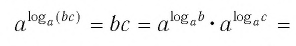
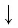 по свойствам степени
по свойствам степени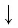
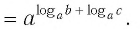
Таким образом, имеем:
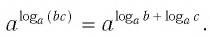
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
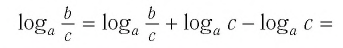
 I используя равенство (1), получим
I используя равенство (1), получим 

Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство

Доказательство:
По основному логарифмическому тождеству
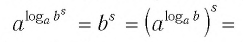
 по свойствам степени
по свойствам степени 

Таким образом, имеем
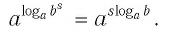
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 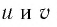 одного знака, то имеет место равенство
одного знака, то имеет место равенство

Следствие 2. При любом целом 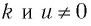 имеет место равенство
имеет место равенство
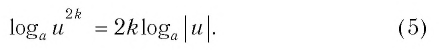
Пример №1
Найти значение выражения:
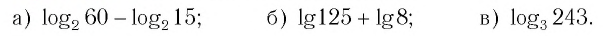
Решение:
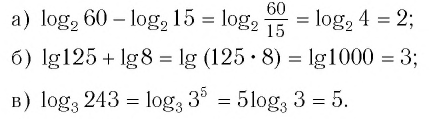
Ответ: 
Теорема:
 При любых значениях
При любых значениях 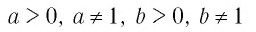 и
и  верно равенство
верно равенство

Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
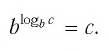
Прологарифмировав левую и правую части этого тождества по основанию а, получим
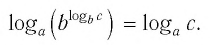
Применив тождество (3), имеем
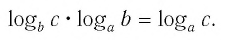
Так как  Поэтому левую и правую части этого равенства можно разделить на
Поэтому левую и правую части этого равенства можно разделить на  В результате получим тождество (6).
В результате получим тождество (6). 
Способ 2. Пусть 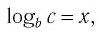 тогда
тогда  Логарифмируя обе части этого равенства по основанию а, получаем
Логарифмируя обе части этого равенства по основанию а, получаем
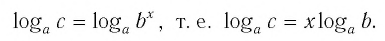
Откуда имеем
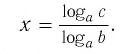
Итак, 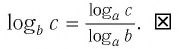
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула

(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если 

Решение:

 согласно тождеству (6) имеем
согласно тождеству (6) имеем
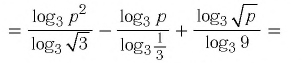
 используя тождество (3), получим
используя тождество (3), получим 

 используя тождество (1), имеем
используя тождество (1), имеем

 с учетом условия
с учетом условия 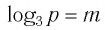 получим
получим

6)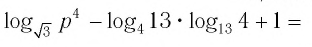
 на основании тождеств (6) и (7) получим
на основании тождеств (6) и (7) получим
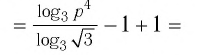
 по тождеству (3) и с учетом условия имеем
по тождеству (3) и с учетом условия имеем
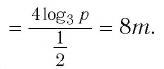
Ответ: 
Следствие 3. Имеют место тождества:

Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение 
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:

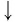 по свойству (2) логарифмов имеем
по свойству (2) логарифмов имеем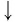

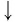 воспользовавшись формулой (7), получим
воспользовавшись формулой (7), получим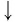
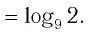
Ответ: 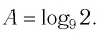
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 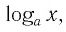 где х — переменная, а — постоянная,
где х — переменная, а — постоянная, 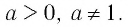 Это выражение имеет смысл при любом значении х 0 и не имеет смысла при любом значении
Это выражение имеет смысл при любом значении х 0 и не имеет смысла при любом значении 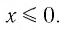 Таким образом, естественной областью определения выражения
Таким образом, естественной областью определения выражения 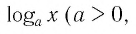
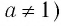 является множество всех положительных действительных чисел, т. е. промежуток
является множество всех положительных действительных чисел, т. е. промежуток 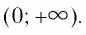
Определение:
Логарифмической функцией называется функция вида 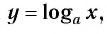 где а — постоянная,
где а — постоянная, 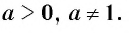
Область определения логарифмической функции — это естественная область определения выражения 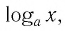 т.е. множество
т.е. множество 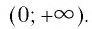
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции  расположен справа от оси Оу и пересекает ось Ох в точке (1; 0).
расположен справа от оси Оу и пересекает ось Ох в точке (1; 0).
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции  при а 1 (рис. 35). График функции
при а 1 (рис. 35). График функции  расположен справа от оси Оу и пересекает ось Ох в точке (1; 0) (см. рис. 34).
расположен справа от оси Оу и пересекает ось Ох в точке (1; 0) (см. рис. 34).
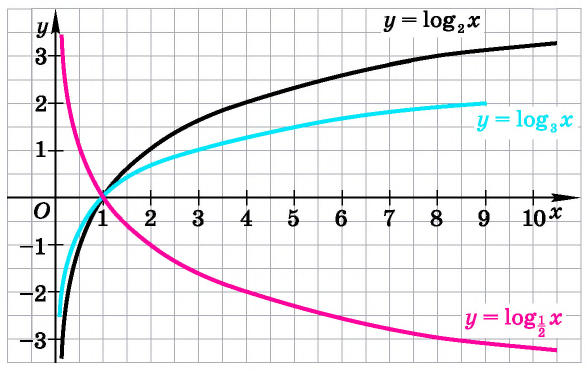
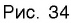

Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 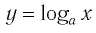 при 0
при 0
Теорема (о свойствах логарифмической функции 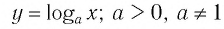 )
)
Областью определения логарифмической функции является интервал 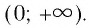
Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
Значение аргумента х = 1 является нулем логарифмической функции.
6. При а 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале  И при 0
И при 0 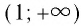 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).
Логарифмическая функция не является ни четной, ни нечетной.
При а 1 логарифмическая функция возрастает на всей области определения. При 0
Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 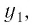 лежащей на оси Оу, найдется такая точка
лежащей на оси Оу, найдется такая точка 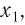 принадлежащая интервалу
принадлежащая интервалу 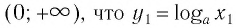 (свойство 2).
(свойство 2).
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а 1 график логарифмической функции лежит в IV координатном угле, когда 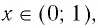 и лежит в I координатном угле, когда
и лежит в I координатном угле, когда 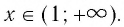 При 0
При 0 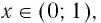 и лежит в IV координатном угле, когда
и лежит в IV координатном угле, когда 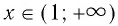 (свойство 6).
(свойство 6).
Область определения логарифмической функции — интервал  поэтому логарифмическая функция не является ни четной, ни нечетной, ни периодической (свойства 7, 9).
поэтому логарифмическая функция не является ни четной, ни нечетной, ни периодической (свойства 7, 9).
На рисунке 35 видно, что при а 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 а
Пусть точка  лежит на графике функции
лежит на графике функции 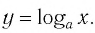 Это значит, что верно числовое равенство
Это значит, что верно числовое равенство 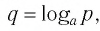 следовательно, согласно определению логарифма верно числовое равенство
следовательно, согласно определению логарифма верно числовое равенство 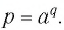 В свою очередь, последнее равенство означает, что точка
В свою очередь, последнее равенство означает, что точка 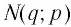 лежит на графике функции
лежит на графике функции 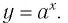
Заметим, что точки  симметричны относительно прямой
симметричны относительно прямой  Таким образом, каждой точке М на графике функции
Таким образом, каждой точке М на графике функции 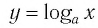 соответствует симметричная ей относительно этой прямой точка N на графике функции
соответствует симметричная ей относительно этой прямой точка N на графике функции 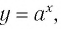 и наоборот. Следовательно, графики функций
и наоборот. Следовательно, графики функций 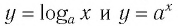 симметричны относительно прямой у = х (рис. 37).
симметричны относительно прямой у = х (рис. 37).
Последнее утверждение дает возможность, зная график функции  изобразить график функции
изобразить график функции 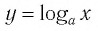 (не используя построение по точкам).
(не используя построение по точкам).
▲ Симметричность графиков функций  относительно прямой у=х означает, что эти функции взаимно обратны.
относительно прямой у=х означает, что эти функции взаимно обратны.
Функции 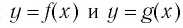 называются взаимно обратными, если для любого
называются взаимно обратными, если для любого 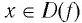 верно равенство
верно равенство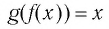 и для любого
и для любого 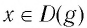 верно равенство
верно равенство 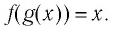
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 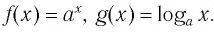 Тогда
Тогда 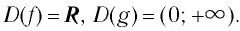
Для любого 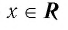
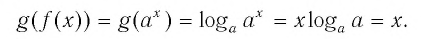
Для любого 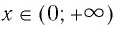

Покажем, что графики взаимно обратных функций  симметричны относительно прямой у = х.
симметричны относительно прямой у = х.
Пусть точка  лежит на графике функции
лежит на графике функции 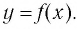 Это означает, что верно числовое равенство
Это означает, что верно числовое равенство 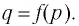 Тогда по определению взаимно обратных функций
Тогда по определению взаимно обратных функций 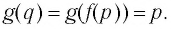 А равенство
А равенство  означает, что точка
означает, что точка 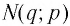 лежит на графике функции
лежит на графике функции 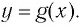
Таким образом, каждой точке М на графике функции 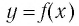 соответствует симметричная относительно прямой у = х точка N на графике функции
соответствует симметричная относительно прямой у = х точка N на графике функции  и наоборот. Следовательно, графики функций
и наоборот. Следовательно, графики функций 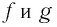 симметричны относительно прямой
симметричны относительно прямой 
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида  Например:
Например:  А какой корень имеет уравнение
А какой корень имеет уравнение  Графическим методом можно убедиться, что оно имеет единственное решение (рис. 28). Это число больше 2 и меньше 3, но как его записать?
Графическим методом можно убедиться, что оно имеет единственное решение (рис. 28). Это число больше 2 и меньше 3, но как его записать?
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 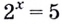 является число, которое записывают в виде
является число, которое записывают в виде 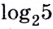 и читают «логарифм числа 5 по основанию 2».
и читают «логарифм числа 5 по основанию 2».
Рассмотрим общий случай-.
Пусть 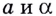 — действительные числа;
— действительные числа; 
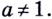 Если
Если 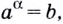 то число
то число 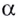 называют логарифмом числа
называют логарифмом числа 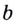 по основанию
по основанию 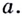
Логарифмом числа 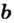 по основанию
по основанию  называют показатель степени, в которую нужно возвести число
называют показатель степени, в которую нужно возвести число 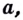 чтобы получить
чтобы получить 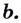
Логарифм числа 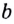 по основанию
по основанию  обозначают символом
обозначают символом 
Примеры:
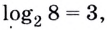 так как
так как 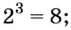
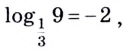 так как
так как 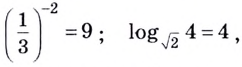 так как
так как 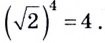
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 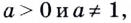 то область определения показательной функции
то область определения показательной функции 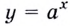 — множество всех действительных чисел
— множество всех действительных чисел 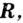 а область значений — множество всех положительных действительных чисел. Поэтому при таких значениях
а область значений — множество всех положительных действительных чисел. Поэтому при таких значениях 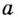 для любого положительного числа
для любого положительного числа  найдётся такое
найдётся такое 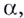 что
что 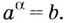 Другими словами: при любом основании
Другими словами: при любом основании 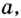 где
где  существует логарифм каждого положительного числа. Логарифм отрицательного числа и нуля не существует.
существует логарифм каждого положительного числа. Логарифм отрицательного числа и нуля не существует.
Полезно помнить, что для каждого 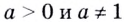
 (почему?).
(почему?).
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если  Это разные записи одной зависимости. Из них следует равенство
Это разные записи одной зависимости. Из них следует равенство
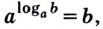
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных 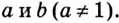
Например: 
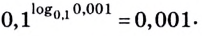
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например: 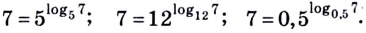
Докажем ещё несколько важных свойств логарифмов (для положительных 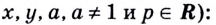
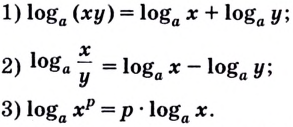
1) По основному логарифмическому тождеству и основному свойству степени
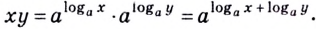
Итак, 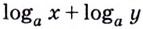 — показатель, в который нужно возвести число
— показатель, в который нужно возвести число 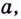 чтобы получить
чтобы получить 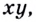 то есть
то есть
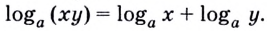
Эту формулу можно обобщить на три и более множителя:

Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
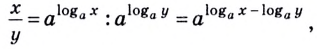
отсюда
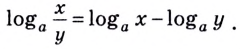
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества  в степень
в степень 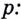
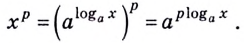
Итак,
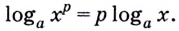
Доказанные формулы можно использовать и справа налево, например:

В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
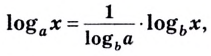
где 
Докажем эту формулу. Поскольку положительные числа 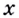 и
и 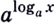 равны, то равны и их логарифмы по основанию
равны, то равны и их логарифмы по основанию  Поэтому
Поэтому
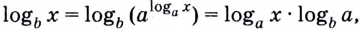 откуда и следует доказываемая формула.
откуда и следует доказываемая формула.
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
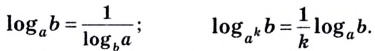
Докажите их самостоятельно.
Пример №4
Упростите выражение 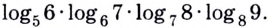
Решение:
Сведём все логарифмы к основанию 5. Имеем:
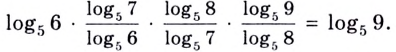
Особенно часто используют логарифмы по основаниям 10 и 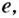 их называют десятичными и натуральными логарифмами. Вместо
их называют десятичными и натуральными логарифмами. Вместо 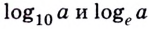 пишут соответственно
пишут соответственно 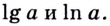
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
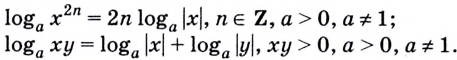
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:

Докажите их самостоятельно.
Пример №5
Вычислите: 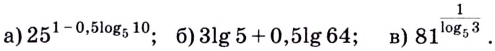
Решение:
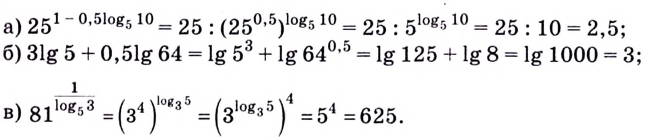
Пример №6
Решите уравнение: 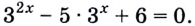
Решение:
Пусть 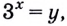 тогда
тогда 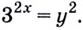 Подставим
Подставим 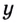 в данное уравнение.
в данное уравнение.
Получим: 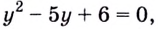 отсюда
отсюда 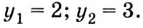
Поскольку 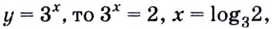 или
или 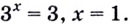
Ответ. 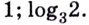
Пример №7
Найдите 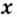 из равенства:
из равенства:
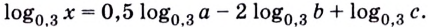
Решение:

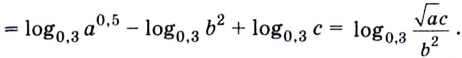
Поскольку 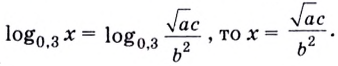
Ответ. 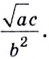
Пример №8
Вычислите 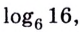 если
если 
Решение:

Ответ. 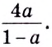








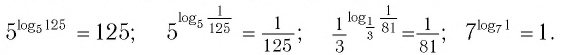 Основное логарифмическое тождество позволяет данное число b представить в виде степени с любым положительным основанием.
Основное логарифмическое тождество позволяет данное число b представить в виде степени с любым положительным основанием.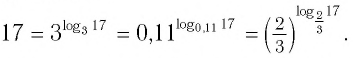

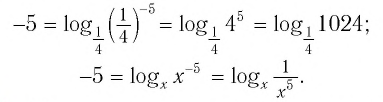
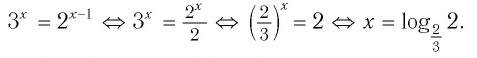
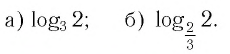
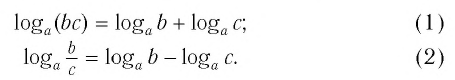

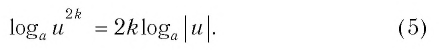
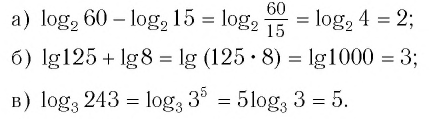
 При любых значениях
При любых значениях 
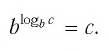
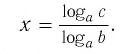


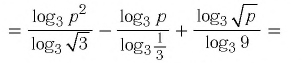


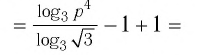
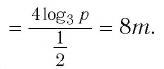







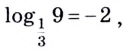 так как
так как 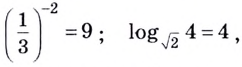 так как
так как