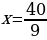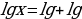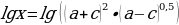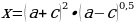Тема: " ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ ВЫРАЖЕНИЙ"
План:
-
Логарифмирование выражений
-
Потенцирование выражений
-
Выполнение упражнений
-
Самостоятельная работа
Логарифмирование выражений
Логарифмирование – это нахождение логарифмов заданных чисел или выражений.
Прологарифмировать выражение – это значит выполнить следующий алгоритм:
-
Взять данное выражение в скобки и перед ними поставить знак логарифма по заданному основанию
-
Используя свойства логарифмов, необходимо убрать внутри логарифма такие действия, как возведение в степень, возведение в корень, умножение и деление
Пример: прологарифмировать выражение 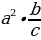 по основанию 10
по основанию 10
Решение: 1. Взять данное выражение в скобки и перед ними поставить знак логарифма по заданному основанию
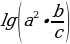
2.внутри логарифма находится умножение, возведение в степень 2 и деление. Избавимся от них по свойствам сложения и вычитания логарифмов, а также умножение числа на логарифм. Получим
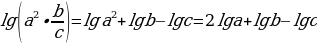
Вывод: логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных
Потенцирование выражений
Потенцирование – это преобразование, обратное логарифмированию. Применяется при решении логарифмических уравнений
Потенцировать выражение – это значит освобождаться от знаков логарифмов в процессе решения логарифмического выражения. Потенцировать можно только в том случае, когда и в левой и правой частях уравнения стоят по одному логарифму с одинаковыми основаниями и больше никаких действий с ними не производится.
То есть 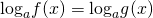 в этом случае можно избавиться от знаков логарифма вместе с основаниями и получим
в этом случае можно избавиться от знаков логарифма вместе с основаниями и получим
f(x)=g(x)
Пример: потенцировать выражение log2 3x = log2 9
Решение: так как основания логарифмов одинаковые и в каждой части выражения стоят по одному логарифму и никаких действий больше нет, то избавляемся от логарифмов
3х = 9.
В результате получаем простое уравнение, которое решается за несколько секунд:
х = 9 : 3 = 3.
Выполнение упражнений
-
Прологарифмировать по основанию 10 выражение 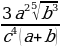
Решение: 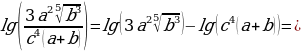
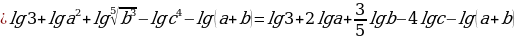
Здесь мы использовали формулу 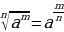
-
Найти х, используя свойства логарифмов и потенцирование
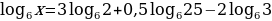
Решение: в правой части выражения больше одного логарифма и есть еще дополнительные действия – это умножение числа на логарифм
используем свойство 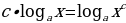
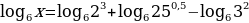
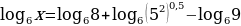
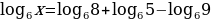
Используем свойства сложения и вычитания логарифмов
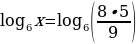
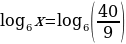 потенцировать можно
потенцировать можно
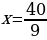
-
Выполните потенцирование выражения:
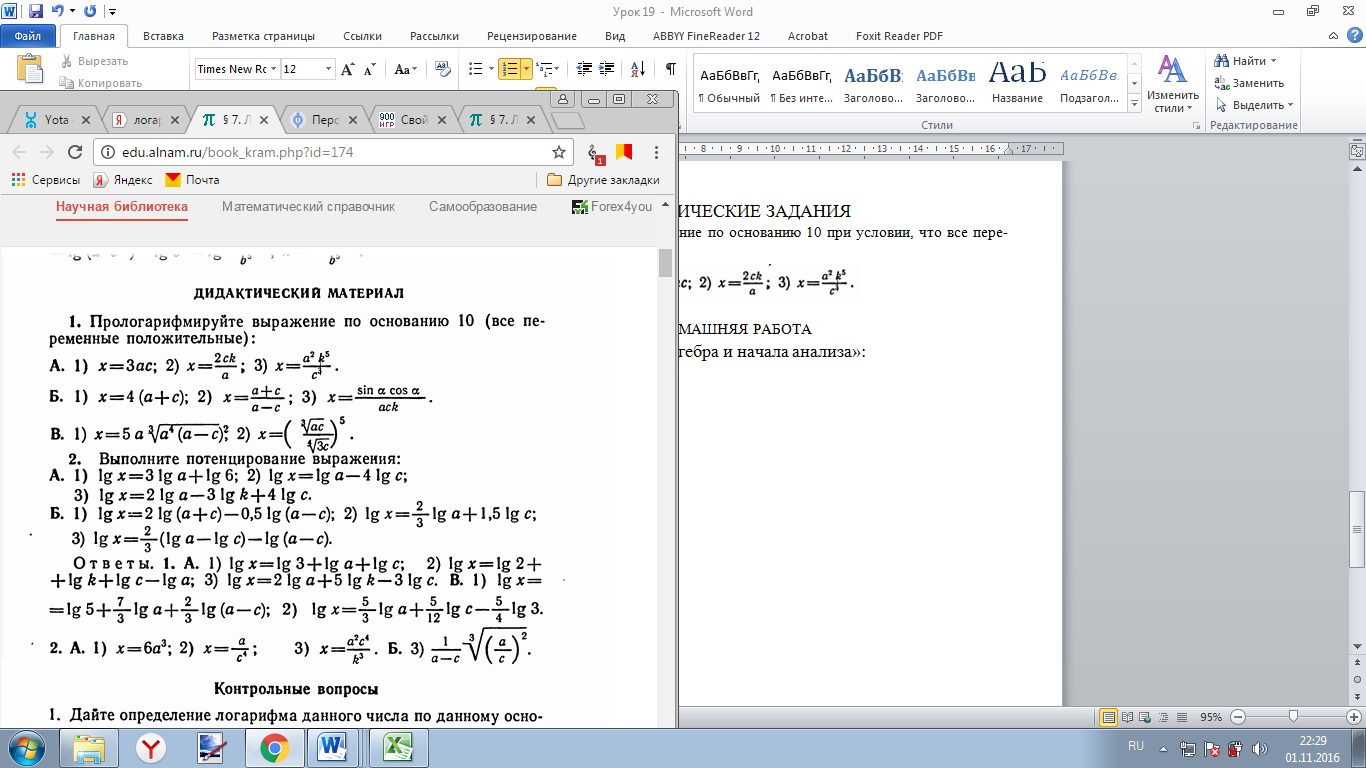
Решение:
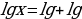
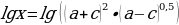
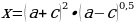
Самостоятельная работа
-
Решить из учебника №491(а, г), №492(а), №493(б), №497(в, г) стр. 237
-
Решить из учебника №7(под цифрой 3 под буквой а) стр. 274







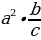 по основанию 10
по основанию 10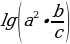
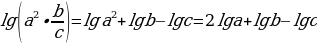
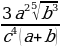
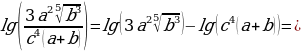
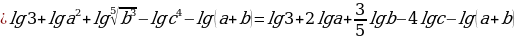
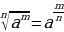
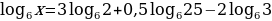
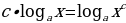
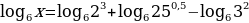
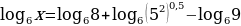
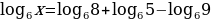
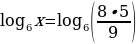
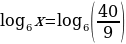 потенцировать можно
потенцировать можно