Дата:
Предмет: информатика
Учитель:
Класс:
Тема урока: Логические схемы.
Цель урока: Формирование у обучающихся навыков построения логических схем для выражений.
Логические схемы
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 - 1933), кстати, несколько лет, работавший в России, писал еще в 1910 году: «...Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе - система чисто качественных... «посылок», ничего не оставляющая желать в отношении сложности и запутанности... правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А.Гавриловым (1903 - 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет... В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.

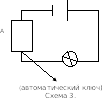

На рисунках контакты обозначены латинскими буквами А и В. Введем обозначения: 1 -контакт замкнут, 0 - контакт разомкнут. Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ».
Заполняем таблицу по ходу объяснения материала.
| Конъюнкция | Дизъюнкция | Инверсия |
| 
| 
| 
|
| А 1 1 0 0 | В 1 0 1 0 | Результат 1 0 0 0 | А 1 1 0 0 | В 1 0 1 0 | Результат 1 1 1 0 | А 1 0 | ¬А 0 1 |
| Конъюнктор | Дизъюнктор | Инвертор |
| 
| 
| 
|
Докажем это, рассмотрев состояния схем при различных состояниях контактов.
Схема 1 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
Первый контакт в положении «включено» второй в положении «выключено». Ток не идет, лампочка не горит.
Обратная ситуация. Лампочка не горит.
Оба контакта в положении «выключено». Тока нет. Лампочка не горит.
Вывод: первая схема действительно реализует логическую операцию «И».
Схема 2 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
Первый контакт в положении «включено» второй в положении «выключено». Ток идет, лампочка не горит.
Обратная ситуация. Лампочка горит.
Оба контакта в положении «выключено». Тока нет. Лампочка не горит.
Вывод: вторая схема действительно реализует логическую операцию «ИЛИ».
Схема 3 (составляем в основной таблице таблицу истинности).
В этом устройстве в качестве переключателя используется автоматический ключ. когда тока на нем нет, пластинка замыкает контакты и лампочка горит. если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит.
Вывод: третья схема действительно реализует логическую операцию «НЕ».
Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом, становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
3. Построение логических схем
Правило построения логических схем:
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей вентиль.
Соединить вентили в порядке выполнения логических операций.
Пример 1
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X.
Две переменные - X и Y.
Две логические операции:
2 1
X v Y & X.
3) Строим схему:


Ответ: 1v 0 & 1 = 1.
Пример 2
Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения для X=1, Y=0.
Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и инверсия:
1 4 3 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком логических операций:
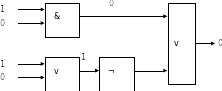
Вычислим значение выражения: F=1&0v ¬ (0v1) =0.
Закрепление изученного материала
Постройте логическое выражение по логической схеме:







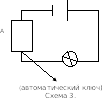








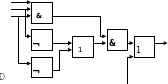 )
)
 )
)









