Математическая игра "Абака №2"

Правила игры «Абака».

Математическая абака (или «математический покер») — очень динамичная и интересная командная игра.

В игре участвуют двух команды, состоящие из 4-5 человек . Все задачи выдаются для решения всем командам одновременно. Основным зачетным показателем является общее количество набранных очков (включая призовые очки — «бонусы»). В случае равенства очков у нескольких команд, более высокое место занимает команда, набравшая большую сумму бонусов. При равенстве и этого показателя — команды считаются разделившими место.

Каждой команде предлагается для решения 6 тем, по 6 задач в каждой теме. В каждой задаче принимается точный и полный ответ. Задачи каждой темы сдаются командами по порядку, от 1-й до 6-й (например, у команды не возьмут ответ на четвертую задачу, пока она не сдала ответы на первые три). На каждую задачу отводится один «подход» (одна попытка сдать ответ). Если команда предъявила правильный ответ на задачу, она получает за это столько очков, какова «стоимость» задачи, а если неправильный или, неполный — 0 очков. «Стоимость» первой задачи каждой темы — 10 очков, второй — 20, ..., шестой — 60 очков. (Таким образом, не считая бонусов, команда может заработать за решение задач до 6 • 210 = 1260 очков.)

Каждая команда дополнительно может заработать бонусные очки:

• за правильное решение всех задач одной темы («бонус-горизонталь») — 50 очков;

• за правильное решение задач с одним и тем же номером во всех темах («бонус-вертикаль») — «стоимость» задачи с этим номером.

На решение задач отводится заранее определенное время (40 минут). Игра для команды заканчивается, если у нее закончились несданные задачи или истекло общее время, отведенное для игры.

Г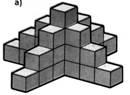еометрия в пространстве.

№1 (10баллов). Сколько кубиков использовано для построения башни?

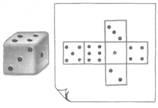
№2 (20 баллов). На рисунке изображены игральный кубик и его развертка. Какое число находится на нижней грани кубика?

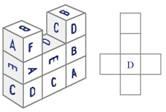
№3 (30 баллов). Перед вами постройка, состоящая из восьми одинаковых кубиков. Определите расположение букв на развертке кубика.

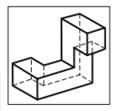№4 (40 баллов). На каком(их) рисунке(ах) снизу изображена та же фигура, что и на рисунке А?

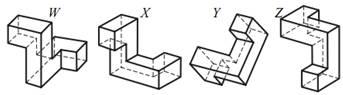
Рисунок А

№5 (50 баллов). Объемная фигура собрана из одинаковых кубиков, соединенных между собой гранями. Какое минимальное количество кубиков необходимо добавить, чтобы соединить концы фигуры таким же способом?

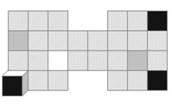
№6 (60 баллов). Определите путь, по которому необходимо перекатить по полю кубик с исходного положения в правую верхнюю ячейку поля. Противоположные грани кубика имеют одинаковый цвет. Перекатываясь по полю, кубик должен по одному разу коснуться своими гранями всех ячеек, которые закрашенные под цвет граней кубика. Заштрихованных ячеек кубик может касаться любой своей гранью, но также один раз. По всем заштрихованным ячейкам кубик перекатывать не обязательно.

Ответы :