Линейной функцией называется функция вида 
В уравнении функции число  , которое мы умножаем на
, которое мы умножаем на  называется коэффициентом наклона.
называется коэффициентом наклона.
Например, в уравнении функции 
 ;
;
в уравнении функции 
 ;
;
в уравнении функции 
 ;
;
в уравнении функции 
 .
.

Графиком линейной функции является прямая линия.
1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции.
Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции  , удобно взять
, удобно взять  и
и  , тогда ординаты эти точек будут равны
, тогда ординаты эти точек будут равны  и
и  .
.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции  :
:

2. В уравнении функции  коэффициент
коэффициент  отвечает за наклон графика функции:
отвечает за наклон графика функции:
- если

 , то график наклонен вправо
, то график наклонен вправо
- если

 , то график наклонен влево
, то график наклонен влево
Коэффициент  отвечает за сдвиг графика вдоль оси
отвечает за сдвиг графика вдоль оси  :
:
- если

 , то график функции
, то график функции  получается из графика функции
получается из графика функции сдвигом на
сдвигом на  единиц вверх вдоль оси
единиц вверх вдоль оси 
- если
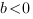
 , то график функции
, то график функции  получается из графика функции
получается из графика функции  сдвигом на
сдвигом на  единиц вниз вдоль оси
единиц вниз вдоль оси 
На рисунке ниже изображены графики функций  ;
;  ;
; 


Заметим, что во всех этих функциях коэффициент  больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение
больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение  , тем круче идет прямая.
, тем круче идет прямая.
Во всех функциях  - и мы видим, что все графики пересекают ось OY в точке (0;3)
- и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций  ;
;  ;
; 


На этот раз во всех функциях коэффициент  меньше нуля, и все графики функций наклонены влево.
меньше нуля, и все графики функций наклонены влево.
Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций  ;
;  ;
; 

Теперь во всех уравнениях функций коэффициенты  равны. И мы получили три параллельные прямые.
равны. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции  (b=3) пересекает ось OY в точке (0;3)
(b=3) пересекает ось OY в точке (0;3)
График функции  (b=0) пересекает ось OY в точке (0;0) - начале координат.
(b=0) пересекает ось OY в точке (0;0) - начале координат.
График функции  (b=-2) пересекает ось OY в точке (0;-2)
(b=-2) пересекает ось OY в точке (0;-2)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции  .
.
Если k<0 и b>0, то график функции  имеет вид:
имеет вид:

Если k>0 и b>0, то график функции  имеет вид:
имеет вид:

Если k>0 и b<0, то график функции  имеет вид:
имеет вид:

Если k<0 и b<0, то график функции  имеет вид:
имеет вид:

Если k=0 , то функция  превращается в функцию
превращается в функцию  и ее график имеет вид:
и ее график имеет вид:

Ординаты всех точек графика функции  равны
равны 
Если b=0, то график функции  проходит через начало координат:
проходит через начало координат:

Это график прямой пропорциональности.
3. Отдельно отмечу график уравнения  . График этого уравнения представляет собой прямую линию, параллельую оси
. График этого уравнения представляет собой прямую линию, параллельую оси  все точки которой имеют абсциссу
все точки которой имеют абсциссу  .
.
Например, график уравнения  выглядит так:
выглядит так:
Внимание! Уравнение  не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

4. Условие параллельности двух прямых:
График функции  параллелен графику функции
параллелен графику функции  , если
, если 
5. Условие перпендикулярности двух прямых:
График функции  перпендикулярен графику функции
перпендикулярен графику функции  , если
, если  или
или 
6. Точки пересечения графика функции  с осями координат.
с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда  . То есть точка пересечения с осью OX имеет координаты (
. То есть точка пересечения с осью OX имеет координаты ( ;0):
;0):

Рассмотрим решение задач.
1. Постройте график функции  , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.
, если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.
В уравнении функции  два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.
два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.
а) Из того, что график функции  параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид
параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид 
б) Нам осталось найти b. Известно, что график функции  проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:
проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:
 отсюда b=-10
отсюда b=-10
Таким образом, нам надо построить график функции 
Точка А(-3;2) нам известна, возьмем точку B(0;-10)
Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).
Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой  . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.
. То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение  и получим систему линейных уравнений.
и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим  . Подставим значение k в первое уравнение системы, и получим b=-2.
. Подставим значение k в первое уравнение системы, и получим b=-2.
Итак, уравнение прямой  .
.
Просмотр содержимого документа
«Математика. Построение графика линейной функции вида y = kx + b.»

Тема «Построение графика
линейной функции вида
у= kx + b »
Обучающее задание:
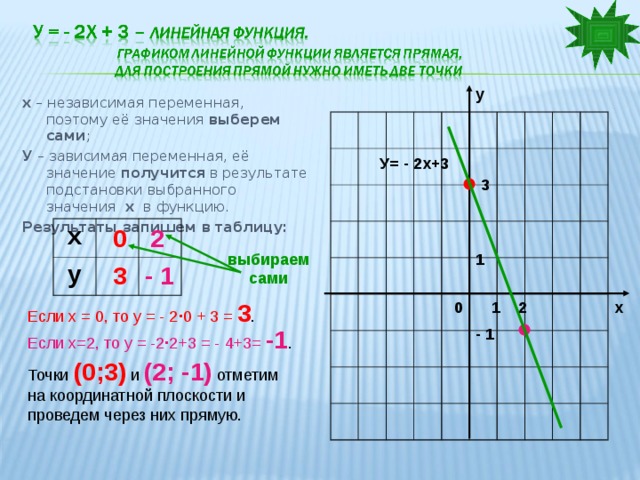
«Построить график функции у = - 2х + 3 »
у= kx + b
Автор презентации:
Хартон М.
у
х – независимая переменная, поэтому её значения выберем сами ;
У – зависимая переменная, её значение получится в результате подстановки выбранного значения х в функцию.
Результаты запишем в таблицу:
У= - 2х+3
3
2
0
х
у
1
выбираем
сами
- 1
3
х
0
Если х = 0, то у = - 2 · 0 + 3 = 3 .
2
1
Если х=2, то у = -2 · 2+3 = - 4+3= -1 .
- 1
Точки (0;3) и (2; -1) отметим
на координатной плоскости и
проведем через них прямую.

Задания для самостоятельного решения: построить графики функций (выполнять в тетради)
1. у = 2х – 2
Ответ:
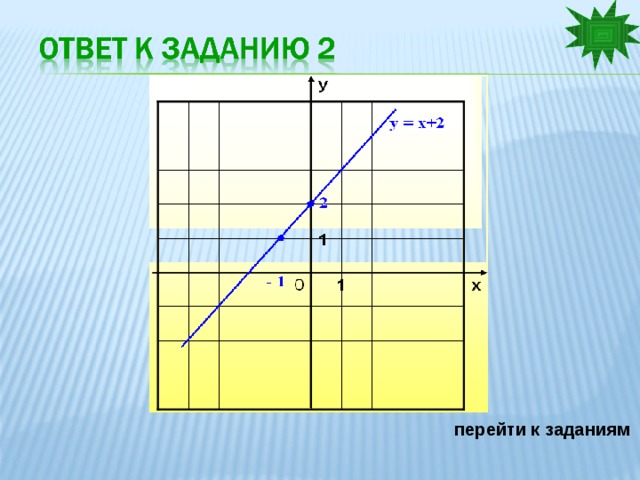
2. у = х + 2
Ответ:
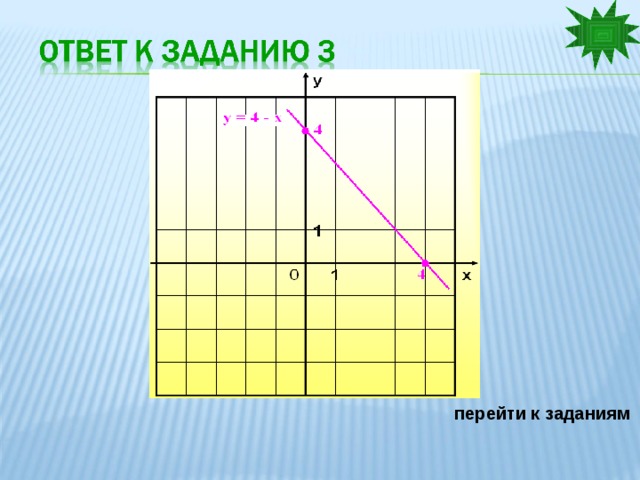
3. у = 4 – х
Ответ:
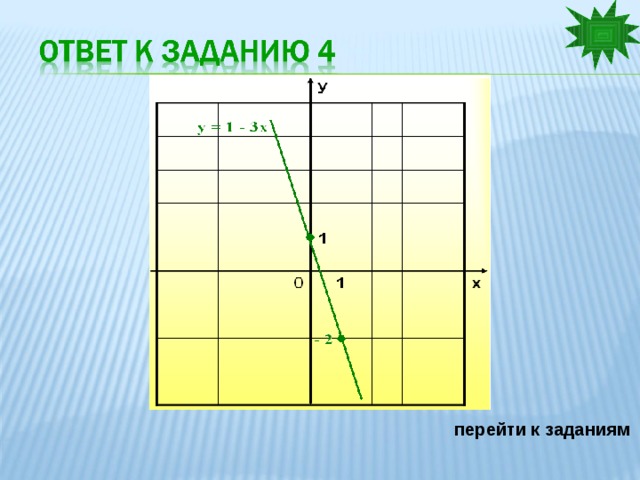
4. у = 1 – 3х
Ответ:
5. Тест
При сверке ответов обратите внимание:
точки, выбранные вами для построения прямой, могут быть другими,
но расположение графиков обязательно должно совпадать
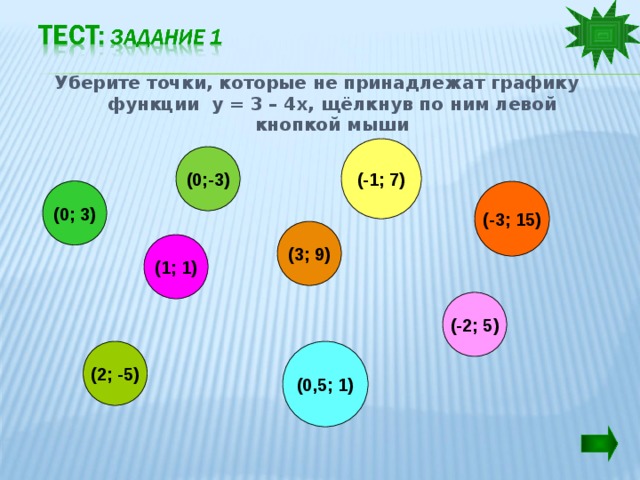
Уберите точки, которые не принадлежат графику функции у = 3 – 4х, щёлкнув по ним левой кнопкой мыши
(-1; 7)
(0;-3)
(0; 3)
(-3; 15)
(3; 9)
(1; 1)
(-2; 5)
(2; -5)
(0,5; 1)
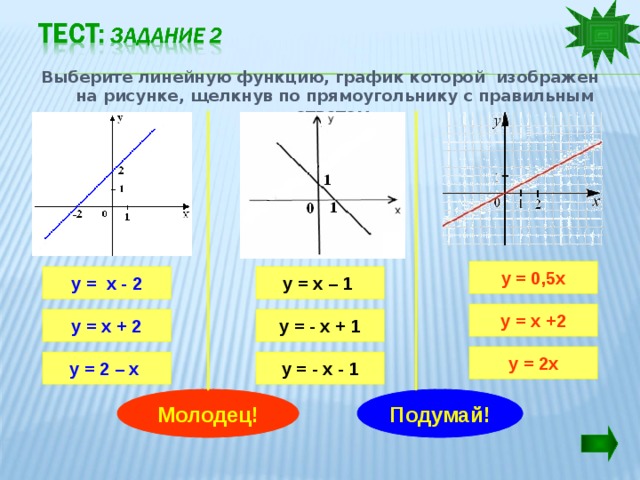
Выберите линейную функцию, график которой изображен на рисунке, щелкнув по прямоугольнику с правильным ответом
у = 0,5х
у = х - 2
у = х – 1
у = х +2
у = - х + 1
у = х + 2
у = 2х
у = - х - 1
у = 2 – х
Молодец!
Подумай!

- Функция вида у = kx + b называется линейной .
- Графиком функции вида у = kx + b является прямая .
- Для построения прямой необходимы только две точки , так как через две точки проходит единственная прямая.


перейти к заданиям
перейти к заданиям
перейти к заданиям
перейти к заданиям









 , которое мы умножаем на
, которое мы умножаем на  называется коэффициентом наклона.
называется коэффициентом наклона.
 ;
;
 ;
;
 ;
;
 .
.
 , удобно взять
, удобно взять  и
и  , тогда ординаты эти точек будут равны
, тогда ординаты эти точек будут равны  и
и  .
.
 отвечает за наклон графика функции:
отвечает за наклон графика функции:

 отвечает за сдвиг графика вдоль оси
отвечает за сдвиг графика вдоль оси  :
:
 сдвигом на
сдвигом на 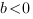
 ;
;  ;
; 

 - и мы видим, что все графики пересекают ось OY в точке (0;3)
- и мы видим, что все графики пересекают ось OY в точке (0;3) ;
; 

 ;
; 





 и ее график имеет вид:
и ее график имеет вид:

 . График этого уравнения представляет собой прямую линию, параллельую оси
. График этого уравнения представляет собой прямую линию, параллельую оси  выглядит так:
выглядит так:
 параллелен графику функции
параллелен графику функции  , если
, если 
 или
или 
 . То есть точка пересечения с осью OX имеет координаты (
. То есть точка пересечения с осью OX имеет координаты ( ;0):
;0):

 отсюда b=-10
отсюда b=-10


 . Подставим значение k в первое уравнение системы, и получим b=-2.
. Подставим значение k в первое уравнение системы, и получим b=-2. .
.





















