Материал к неделе математики

Разбор и решение любого рода математических задач, а в особенности нестандартных, помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам. Я рассмотрю два типа математических софизмов: алгебраические, геометрические

Алгебраические софизмы.

1. «Два неодинаковых натуральных числа равны между собой»

решим систему двух уравнений: х+2у=6, (1)

у=4- х/2 (2)

подстановкой у из 2-го ур-я в 1 по-

лучаем х+8-х=6, откуда 8=6

где ошибка???

Уравнение (2) можно записать как х+2у=8, так что исходная система запишется в виде:

Х+2у=6,

Х+2у=8

В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Графически это означает, что прямые у=3-х/2 и у=4-х/2 параллельны и не совпадают.

Перед тем, Как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

2. «Сочетательное и переместительное свойства алгебраической суммы не имеют места»

Рассмотрим сумму бесконечного числа слагаемых, поочередно равных плюс единице и минус единице, т.е.

S=1-1+1-1+1-1+1-1+1-1+…….. ,(1)

И попробуем найти значение этой суммы.

Сначала поступим следующим образом. Будем объединять слагаемые в пары, начиная со второго слагаемого, ставя перед каждой парой «минус», т.е.

S=1-(1-1)-(1-1)-….=1-0-0-…=1.

Теперь переставим каждое положительное слагаемое той же суммы (1) на место отрицательного и обратно, тогда

S=-1+1-1+1-1+1-…=-1+(1-1)+(1-1)+…=-1+0+0+…=-1.

Итак, по-разному переставляя слагаемые суммы(1), мы пришли к различным значениям этой суммы: 1 и –1, в итоге сумма слагаемых изменяется от перегруппировки слагаемых ,а сочетательное и переместительное свойства алгебраической суммы не имеют места.

Где ошибка?

3. «Дважды два равно пяти».

Обозначим 4=а, 5=b, (a+b)/2=d. Имеем: a+b=2d, a=2d-b, 2d-a=b. перемножим два последних равенства по частям. Получим: 2da-a*a=2db-b*b. Умножим обе части получившегося равенства на –1 и прибавим к результатам d*d. Будем иметь: a ²-2da+d²=b² -2bd+d², или (a-d)(a-d)=(b-d)(b-d), откуда a-d=b-d и a=b, т.е. 2 2=5

Где ошибка?

Из равенства квадратов двух чисел не следует, что сами эти числа равны.

4. «Отрицательное число больше положительного».

Возьмем два положительных числа а и с. Сравним два отношения:

а -а

-с с

Они равны, так как каждое из них равно –(а/с). Можно составить пропорцию:

а -а

-с с

Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае а-с, следовательно, должно быть –ас, т.е. отрицательное число больше положительного.

Где ошибка?

Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны.

Геометрические софизмы.

1. «Через точку на прямую можно опустить два перпендикуляра»

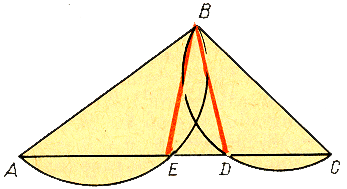Попытаемся "доказать", что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра. С этой целью возьмем треугольник АВС. На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках Е и Д. Соединим точки  Е и Д прямыми с точкой В. Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВДС также прямой. Следовательно, ВЕ  перпендикулярна АС и ВД перпендикулярна АС. Через точку В проходят два перпендикуляра к прямой АС.

Где ошибка?

Рассуждения, о том, что из точки на прямой можно опустить два перпендикуляра, опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ совпадает с ВD. Значит, из одной точки на прямой нельзя опустить два перпендикуляра.

2. « Спичка вдвое длиннее телеграфного столба»

 Пусть  а дм- длина спички и b дм - длина столба. Разность между b и  a  обозначим через c .

Имеем  b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b² - ab = ca + c². Вычтем из обеих частей bc. Получим: b²- ab - bc = ca + c² - bc, или b(b - a - c) = - c(b - a - c), откуда

b = - c, но c = b - a, поэтому b = a - b, или a = 2b.    

Где ошибка?

В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

3. «Катет равен гипотенузе»

Угол С равен 90^о, ВД - биссектриса угла СВА, СК = КА, ОК перпендикулярна СА, О - точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС. Имеем: треугольник LВО равен треугольнику МВО, ВL = ВМ, ОМ = ОL = СК = КА, треугольник КОА равен треугольнику ОМА (ОА - общая сторона, КА = ОМ, угол ОКА и угол ОМА - прямые), угол ОАК = углу МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС.

Где ошибка???

Рассуждения, о том, что катет равен гипотенузе опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного  перпендикуляра к катету АС, находится вне треугольника АВС.