Материал к уроку "Параллелограмм и его свойства"

Параллелограмм (от греч parallelos – параллельный и gramma – начертание).

Параллелограмм (от греч parallelos – параллельный и gramma – линия).

Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

A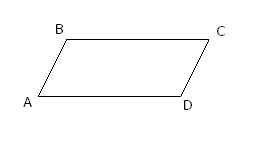 BІІCD

BCІІAD

С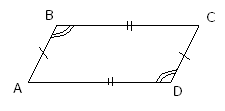 войство параллелограмма.

1. В параллелограмме противоположные стороны равны и противоположные углы равны.

AB=CD

BC=AD

B=

2. Диагонали параллелограмма точкой пересечения делятся пополам.

BO=OD

AO=OC

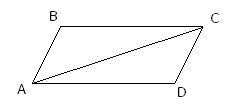
3. Диагональ делит параллелограмм на два равных треугольника.

∆ABC=∆ACD

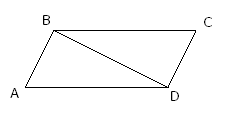
∆ABD=∆BCD

4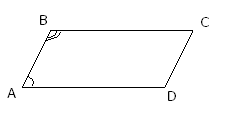 . Сумма соседних углов параллелограмма равна 180⁰.

A+B=180⁰

B+C=180⁰

C+D=180⁰

D+A=180⁰

Дополнительные свойства параллелограмма.

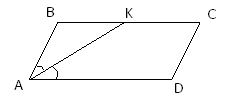
1. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

АК – биссектриса

∆АВК – равнобедренный

2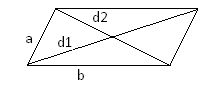 . Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырех сторон.

d₁²+d₁²=2a²+2b²

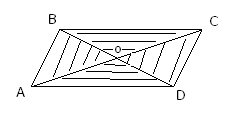
3. Диагонали параллелограмма делят его на четыре равновеликих треугольника.

4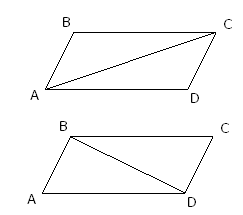 .Каждая диагональ делит параллелограмм на два равных треугольника

5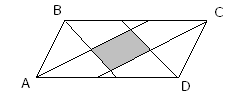 . Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник.

6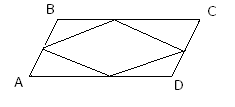 . Середины сторон параллелограмма являются вершинами нового параллелограмма.

7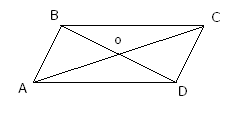 . Параллелограмм – центрально – симметричная фигура. Центром его симметрии является точка пересечения его диагоналей.

Признаки параллелограмма.

1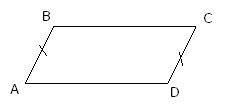 . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

AB=CD

ABIICD

2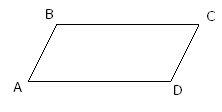 . Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

AB=CD

B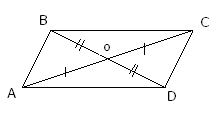 C=AD

3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Частные виды параллелограмма.

1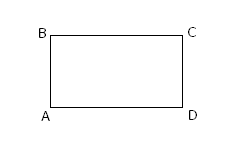 . Прямоугольник.

Прямоугольником называется параллелограмм, у которого все углы прямые.

A=B=C=D=90⁰

Свойства

Д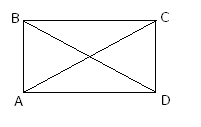 иагонали прямоугольника равны.

AC=BD

Признак

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

2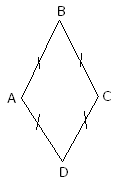 . Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

AB=BC=CD=DA

С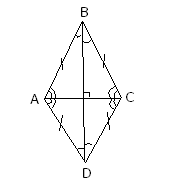 войство

Диагонали ромба взаимно перпендикулярны и делят его пополам.

3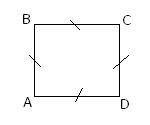 . Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

AB=BC=CD=DA

Свойства

1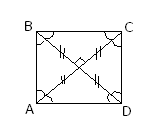 ) Все углы у квадрата прямые.

2) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

AC=BD

С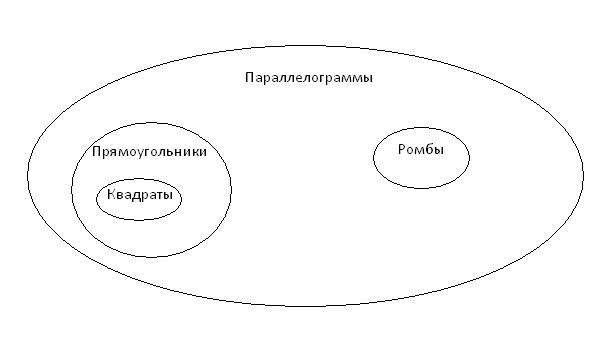 оотношение между рассмотренными видами параллелограмма можно изобразить так.

Периметр и площадь параллелограмма.

Р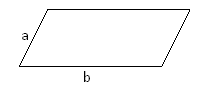 =2а+2b

S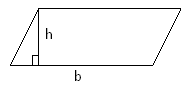 =b·h_b

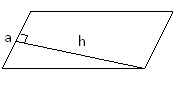
S=a·h_a

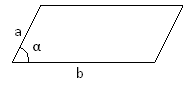
S=a·b·sinα

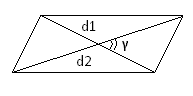
S=½d₁·d₂·sinγ