"Математика в литературных произведениях"

Математика в литературных произведениях

План занятия

1. Вступление.

2. Герои Жюля Верна.

3. Геометрия Гулливера

4. Ошибка Джека Лондона.

5. Башня Гоголя.

6. Холм Пушкина.

7. Домашнее задание: задача Льва Толстого.

8. Заключение.

«В математике есть своя красота, как в живописи и поэзии»

Н. Е. Жуковский

Математика известна с древних времён.

Все архитектурные и художественные шедевры создавались с использованием математики.

Знания математики требовались не только при строительстве, но и при создании литературно – художественных произведений.

Не даром А.С.Пушкин говорил: « Вдохновение нужно в геометрии не меньше, чем в поэзии » .

Грамотное использование математических фактов делает художественное произведение достоверным

и реальным.

Герои Жуля Верна

В романе Жюля Верна «Таинственный остров» описан один из способов измерения высоких предметов .

Прочитаем отрывок .

Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам ,

большее – 500 футам .

По окончании измерений инженер составил следующую запись:

15 : 500 = 10 : х ;

500  10 = 5000;

5000 : 15 = 333,3.

Значит, высота гранитной стены равнялась 333 футам

Свойство подобных

треугольников

Герои Жуля Верна

Один из героев Жюля Верна подсчитывал, какая часть его тела прошла более длинный путь за время кругосветных странствований – голова или ступни ног.

Задача.

Вообразите, что вы обошли земной шар по экватору. Насколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги?

Решение:

Ноги прошли путь 2  R , где R – радиус земного шара.

Верхушка же головы прошла 2  ( R + 1,7) ,

где 1,7 м – рост человека.

Разность путей равна

2  ( R + 1,7) - 2  R = 2   1,7  10, 7 (м).

Голова прошла путь на 10,7 м больше , чем ноги.

Любопытно: в окончательный ответ не входит величина радиуса земного шара.

Результат получится одинаковый и на Земле, и на Юпитере, и на самой маленькой планете.

Геометрия Гулливера

Автор «Путешествия Гулливера» Джонатан Свифт с большой осмотрительностью избежал опасности запутаться в геометрических отношениях.

В стране лилипутов футу соответствовал дюйм , а в стране великанов , наоборот, дюйму – фут .

У лилипутов все люди, все вещи, все произведения природы в 12 раз меньше нормальных, у великанов – во столько же раз больше.

Приходилось решать вопросы:

1. Во сколько раз Гулливер съедал за обедом больше, чем лилипут?

2. Во сколько раз Гулливеру требовалось больше сукна на костюм, нежели лилипуту?

3. Сколько весило яблоко в стране великанов?

• 1. Во сколько раз Гулливер съедал за обедом больше, чем лилипут? 2. Во сколько раз Гулливеру требовалось больше сукна на костюм, нежели лилипуту? 3. Сколько весило яблоко в стране великанов?

Автор «Путешествия» справился с этими задачами .

Раз лилипут ростом меньше Гулливера в 12 раз , то объём его тела меньше в 12  12  12, т. е. в 1728 раз .

Следовательно, для насыщения тела Гулливера нужно в 1728 раз больше пищи, чем для лилипута.

Правильно рассчитал Свифт и количество материала на костюм Гулливеру .

Поверхность его тела больше, чем у лилипута, в 12  12 = 144 раза; во столько же раз нужно ему больше материала.

Ошибка Джека Лондона

Однако в литературных произведениях математические рассуждения не всегда бывают верными.

Роман Джека Лондона «Маленькая хозяйка большого дома» даёт следующий материал для геометрических расчётов:

прочитать отрывок.

Решение

Расчёт неверен: теряется меньше, чем 0,3 всей земли.

Пусть, а - сторона квадрата. Площадь такого квадрата S  = а 2 . Диаметр вписанного круга равен также а , а его площадь S  = .

Пропадающая часть квадратного участка составляет:

S  - S  = а 2 - = (1 - ) а 2 = 0,22 а 2 .

Необработанная часть квадратного поля составляет не 30% , как полагали герои американского романиста, а только 22%.

Башня Гоголя

Что увеличивается быстрее: высота поднятия или дальность горизонта?

Многие думают, что с возвышением наблюдателя горизонт возрастает необычайно быстро. Так думал и Н.В. Гоголь , писавший в статье «Об архитектуре нашего времени».

Прочитать отрывок

«Башни огромные, колоссальные, необходимы в городе…У нас обыкновенно ограничиваются высотой, дающей возможность оглядеть один только город, между тем как для столицы необходимо видеть, по крайне мере на полтораста вёрст во все стороны, и для этого, может быть, один только или два этажа лишних, - и всё изменяется. Объём кругозора по мере возвышения распространяется необыкновенною прогрессией» (1 верста составляет 1,0668 км, 150 верст – 160 км)

Так ли в действительности?

Решение

Рассмотрим формулу:

где l – дальность горизонта,

R – радиус земного шара (  6400км),

h – возвышение глаза наблюдателя над земной поверхностью.

Дальность горизонта растёт

медленнее, чем высота поднятия: она пропорциональна квадратному корню из высоты . Когда возвышение наблюдателя увеличивается в 100 раз, горизонт отодвигается всего только в 10 раз дальше.

Идея сооружения башни, с которой можно было бы видеть, «по крайне мере, на полтораста вёрст», т.е. на 160 км, совершенно несбыточна. Такая башня должна иметь огромную высоту, равную 2 км.

Холм Пушкина

Ошибку делает и А.С.Пушкин , говоря в «Скупом рыцаре» о далёком горизонте, открывающемся с вершины «гордого холма»:

«И царь мог с высоты с весельем озирать

И дол, покрытый белыми шатрами,

И море, где бежали корабли…»

Холм Пушкина

Даже полчища Атиллы не могли бы воздвигнуть холм выше 4,5 м.

Глаз наблюдателя, поместившегося на вершине холма, возвышался бы над почвой на 4,5 + 1,5, т.е. на 6 м, и, следовательно, дальность горизонта равна была бы

Это всего на 4 км больше того, что можно видеть,

стоя на ровной земле .

Задача Льва Толстого

Великий русский писатель Лев Николаевич Толстой проявлял особый интерес к математике и её преподаванию.

Он много лет преподавал начала математики в основанной им же знаменитой Яснополянской школе, написал оригинальную «Арифметику» и «Руководства для учителя».

Своим гостям Л.Н.Толстой нередко предлагал интересные задачи .

Подумайте и решите

«Косцы должны выкосить два луга. Начав косить с утра большой луг, они после полудня разделились: одна половина осталась на первом лугу и к вечеру его докосила, а другая перешла косить на второй луг площадью вдвое меньше первого. Сколько косцов, если известно, что в течение следующего дня оставшуюся часть работы выполнил один косец?».

Прочитайте и найдите

Есть математические рассуждения и в рассказе Л.Н.Толстого

«Много ли человеку земли нужно».

Прочитайте этот рассказ и найдите эти рассуждения.

Обзор литературы показал, что знания по математике нужны не только математикам, но и писателям и поэтам.

«Математика … выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного» (Аристотель)

«- Сегодня нам надо измерить высоту площадки Дальнего Вида, - сказал инженер. 

- Вам понадобится для этого инструмент? – спросил Герберт. - Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.

Взяв прямой шест, футов 12 длиной, инженер измерил его возможно точнее, сравнивая со своим ростом,

который был ему хорошо известен. Герберт же нёс за ним отвес: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса.

Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно пометил колышком.

- Тебе знакомы начатки геометрии? – спросил он Герберта, поднимаясь с земли.

- Да.

- Помнишь свойства подобных треугольников?

- Их сходные стороны пропорциональны.

- …Если мы измерим два расстояния: расстояние от колышка до основания шеста и расстояние от колышка до основания

стены, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены.»

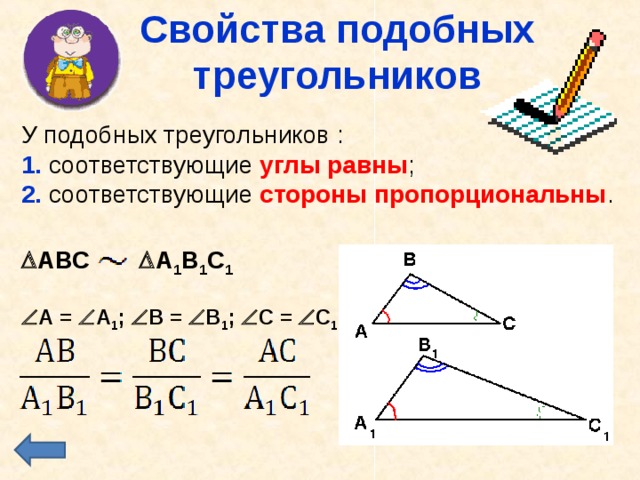
Свойства подобных треугольников

У подобных треугольников :

1. соответствующие углы равны ;

2. соответствующие стороны пропорциональны .

 АВС  А 1 В 1 С 1  А =  А 1 ;  В =  В 1 ;  С =  С 1

«Посреди поля возвышался стальной шест, врытый глубоко в землю. С верхушки шеста к краю поля тянулся трос., прикреплённый к трактору. Механики нажали рычаг – и мотор заработал.

Машина сама двинулась вперёд, описывая окружность вокруг шеста, служившего его центром.

- Чтобы окончательно усовершенствовать машину, - Грэхем, - вам остаётся превратить окружность, которую она описывает, в квадрат.

- Да, на квадратном поле пропадает при такой системе очень много земли.

Грэхем произвёл некоторые вычисления, затем заметил: - Теряем примерно три акра из каждых десяти.

- Не меньше.»

Жюль Верн

1828 - 1905

Это писатель, предвосхитивший возможности современного технического прогресса.

Из 108 гипотез писателя 64 были реализованы.

Увлекавшийся идеями технического прогресса, Ж.Верн был поэтом природы .

Джонатан Свифт

1667 – 1745

Джонатан Свифт прославился как смелый обличитель пороков аристократическо – буржуазного общества Англии начала XVIII в.

Джек Лондон

1876 – 1916

Замечательный американский писатель начала прошлого века Джек Лондон (его настоящее имя - Джон Гриффит) писал о судьбах простых людей своей страны.

В книгах Лондона раскрывается его свободолюбие, уважение к творческой энергии, мужеству, силе человека, видна страстная любовь автора к величественной и неиссякаемой красоте природы.

Гоголь Николай Васильевич

1809 – 1852

Историческая заслуга Гоголя в том, что он «первый взглянул смело и прямо на русскую действительность».

Он хотел видеть русский народ свободным и счастливым.

Смех Гоголя и сегодня не утратил своего художественного обаяния и своей боевой силы.

Александр Сергеевич Пушкин

1799 – 1837

Пушкина по праву считают родоначальником нашей классической литературы, началом всех начал.

Оптимизм Пушкина – это

вера в творчество человеческого разума, в «младую жизнь», идущую на смену старому, отжившему, в победу света и жизни над силами мрака.

Лев Николаевич Толстой

1828 – 1910

Перед глазами Толстого прошло много больших и важных событий. На страницах его произведений запечатлены картины русской жизни за целое столетие – от кануна Отечественной войны 1812 г. до событий, последовавших за революцией 1905 – 1907 г.г.

Толстого сравнивали с горным хребтом, морем, могучим лесом. Поражала личность писателя, многогранная и противоречивая.