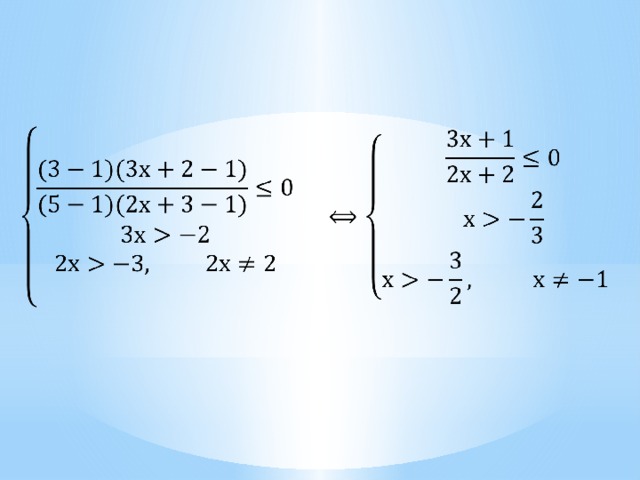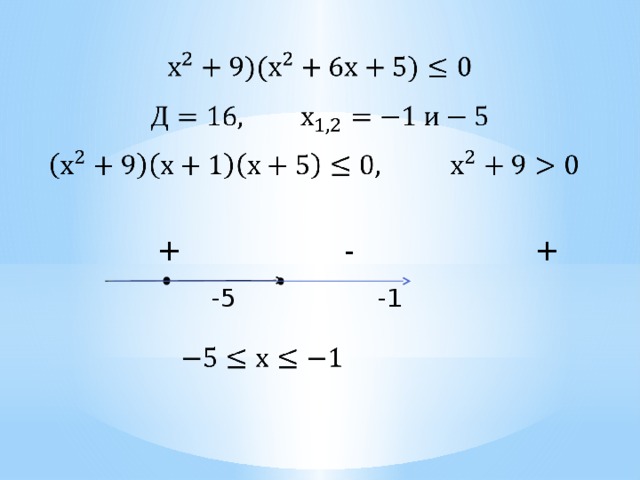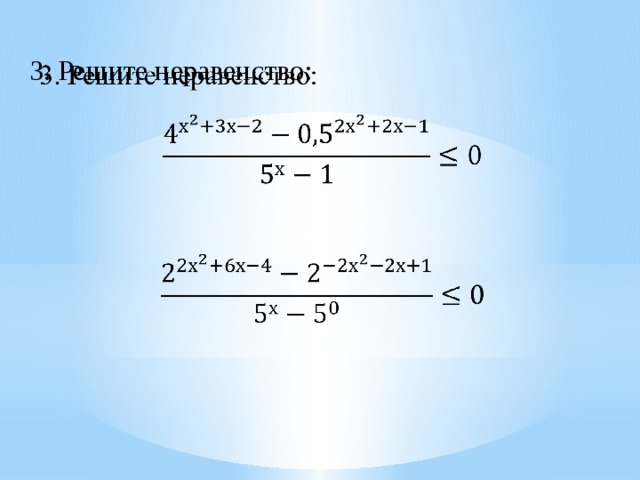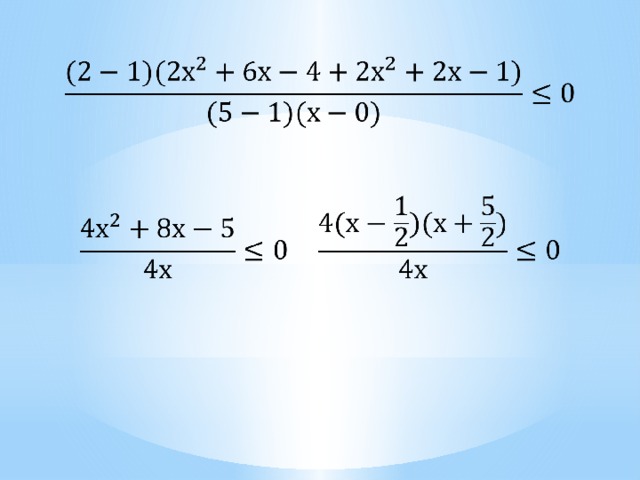Метод рационализации

Цель исследовательской работы:
Изучение теоретического обоснования метода рационализации.
Задачи:
1. Изучить теоремы, которые позволяют заменять сложные выражения на более простые;
2. Рассмотреть примеры применения метода рационализации при решении логарифмических, показательных неравенств;

История метода рационализации
Метод рационализации неравенств известен около 50 лет, встречался под названиями:
- метод декомпозиции,
- метод замены множителей,
- обобщение метода интервалов.

- Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные выражения к равносильному ему рациональному неравенству.
- Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.

Сведение логарифмического неравенства к системе рациональных неравенств
Рассмотрим логарифмическое неравенство вида
-некоторые функции.
где
Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства.
В первом случае , когда основания логарифмов удовлетворяют условию
знак неравенства меняется:
Во втором случае , когда основание удовлетворяет условию
знак неравенства сохраняется:
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь объединить, рационализировать?
Ответ на этот вопрос содержится в следующей теореме.

Теорема 1. Логарифмическое неравенство
равносильно следующей системе неравенств :
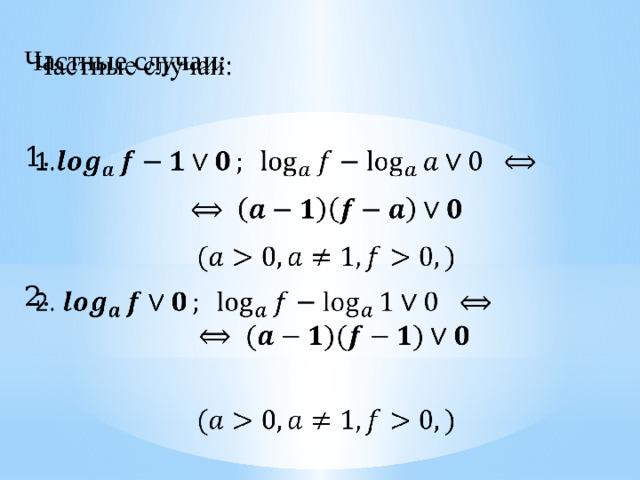
Частные случаи:
1.
2.
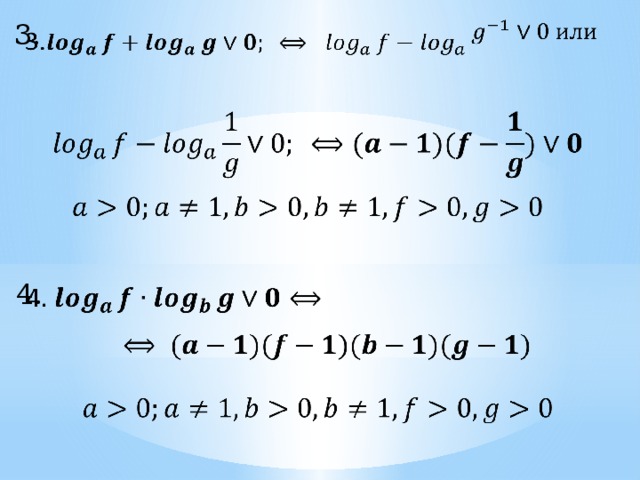
3.
4.
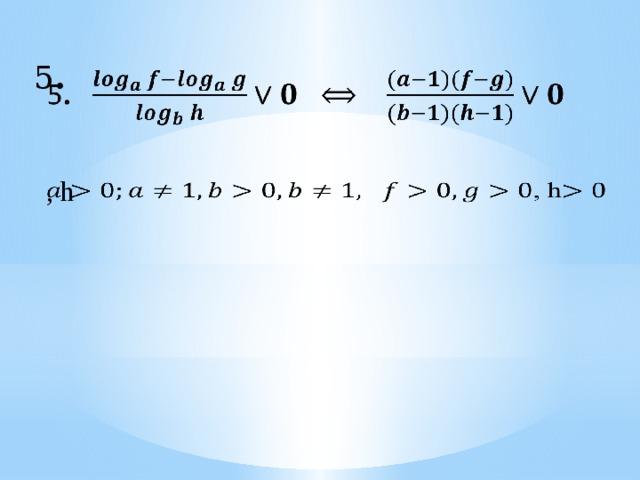
5 .
, h

Сведение показательного неравенства к системе рациональных неравенств
Теперь рассмотрим показательное неравенство вида
- некоторые функции.
И снова вспомним, что традиционное решение такого неравенства приводит к двум случаям . В первом основание степени положительно, но меньше единицы (знак неравенства меняется), во втором случае основание степени больше единицы (знак неравенства сохраняется).
Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.

Теорема 2. Показательное неравенство
равносильно следующей системе неравенств :
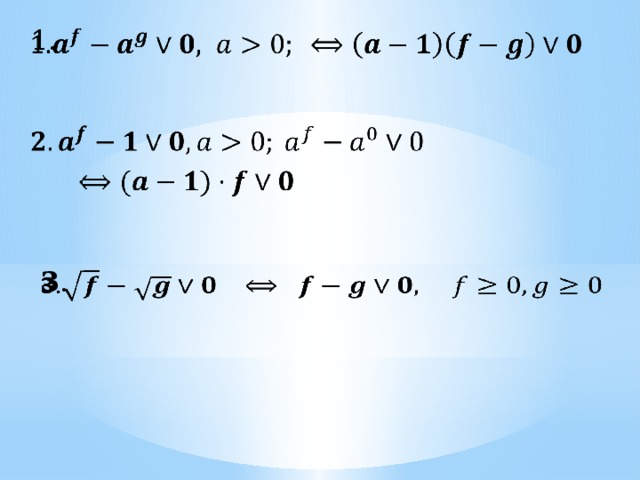
1.
3 .
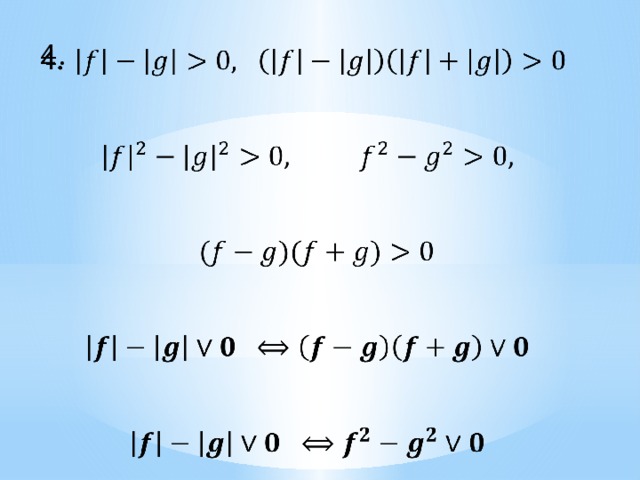
4.

 , Заметим также, вторая и третья строчки таблицы — следствия первой. " width="640"
, Заметим также, вторая и третья строчки таблицы — следствия первой. " width="640"
- где f и g— функции от х,
- h— функция или число,
- V— один из знаков ≤, ,
Заметим также, вторая и третья строчки таблицы — следствия первой.

Примеры решения неравенств
1. Решите неравенство:
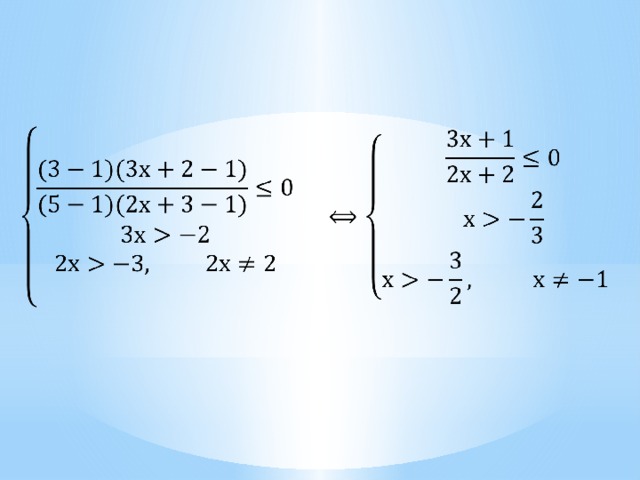


2. Решите неравенство:
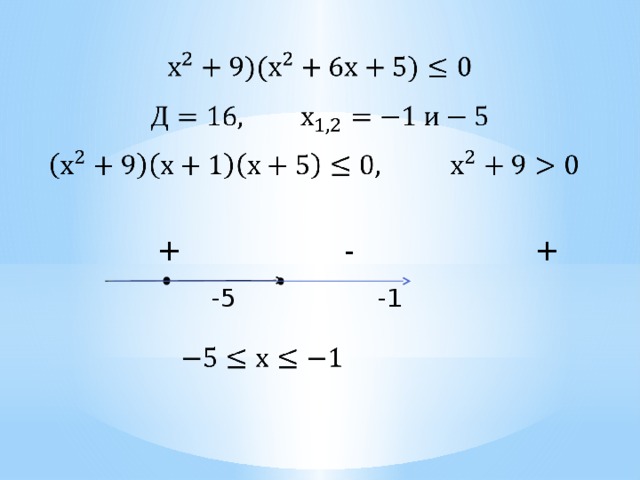
+ - +
-5 -1
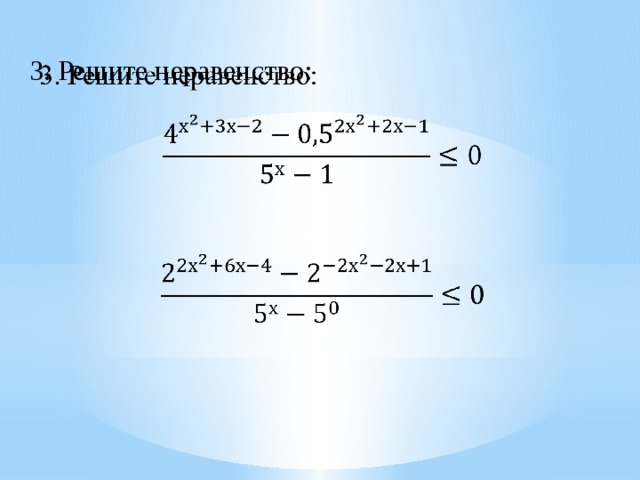
3. Решите неравенство:
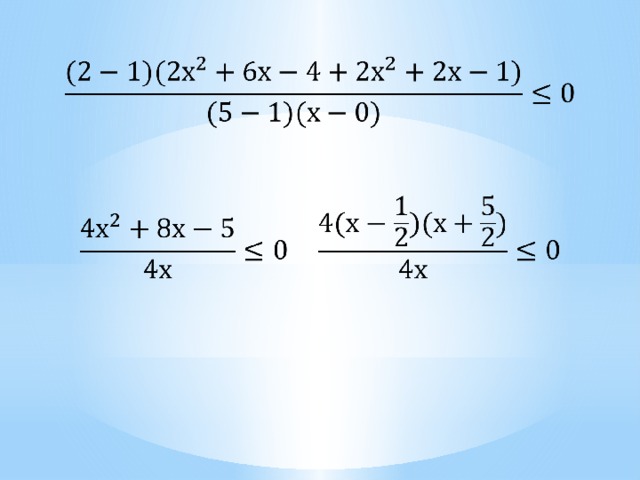
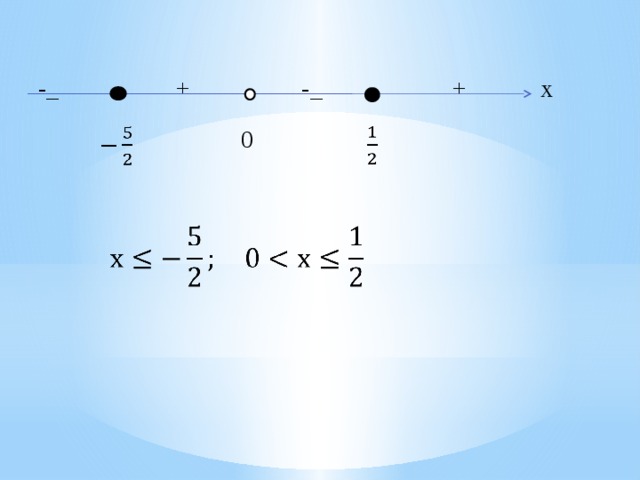
-_ + -_ + х
0













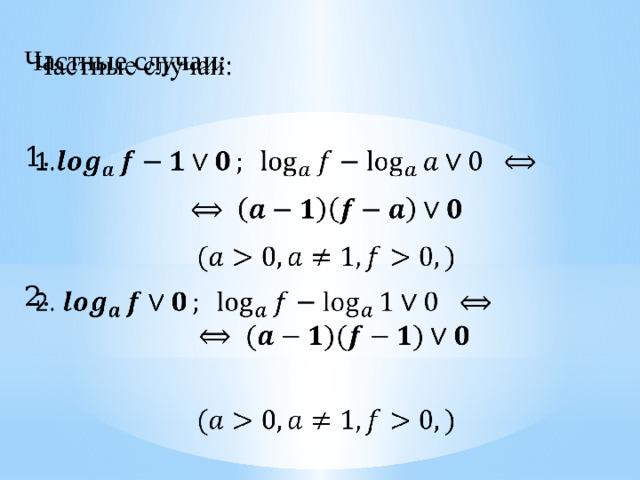
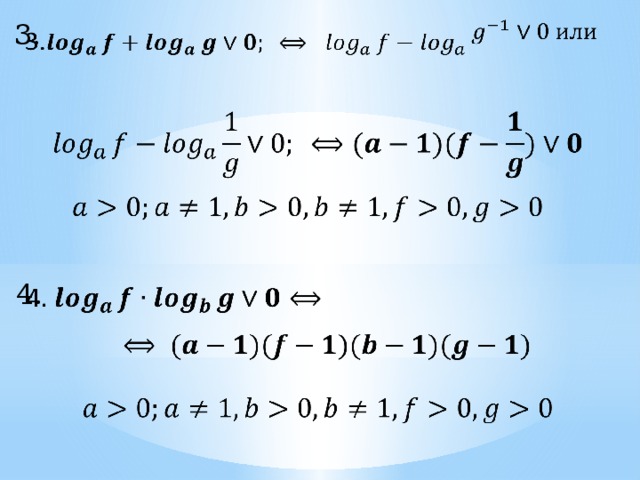
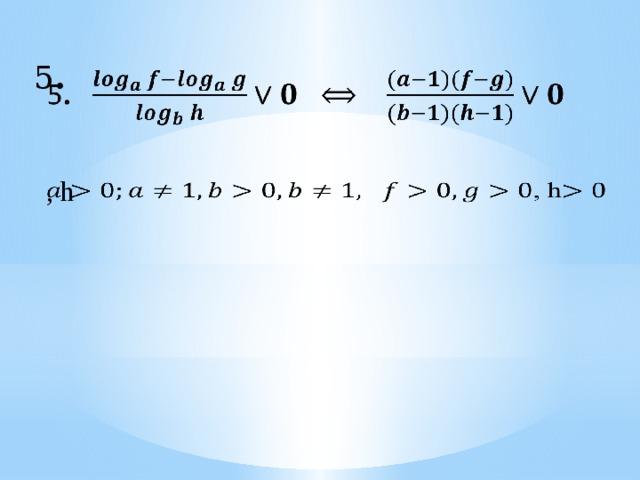


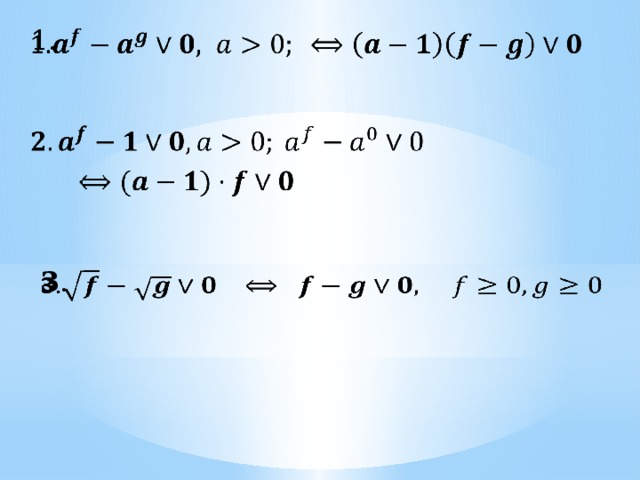
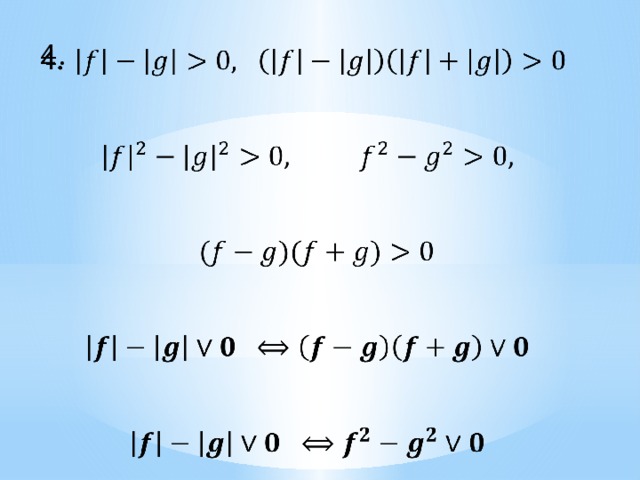

 , Заметим также, вторая и третья строчки таблицы — следствия первой. " width="640"
, Заметим также, вторая и третья строчки таблицы — следствия первой. " width="640"