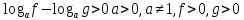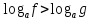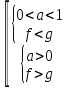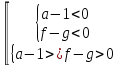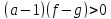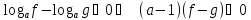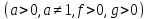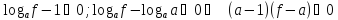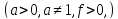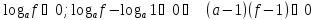Министерство образования и науки Республики Бурятия
Муниципальное автономное образовательное учреждение
«Средняя общеобразовательная школа №5 г.Закаменск»
Школьная научно-практическая конференция «Шаг в будущее»
Секция «Алгебра»
Метод рационализации
Выполнила: Злыгостева Виктория
Ученица 11 «б» класса
Руководитель: Дашеева С.С.
Г. Закаменск
2017год
Содержание
Введение...............................................................................................
Сведение логарифмического неравенства к системе рациональных неравенств............................................................................................
Сведение показательного неравенства к системе рациональных неравенств............................................................................................
. Примеры решения неравенств методом рационализации.........
Заключение..........................................................................................
Литература...........................................................................................
I. Введение
Решение неравенств - важный раздел в математике. Успешное изучение математики невозможно без умения решать разнообразные неравенства, поэтому я решила взять в качестве темы научно-исследовательской работы один из способов решения неравенств – метод рационализации. Разбирая решения сложных неравенств, я увидела, что при решении применяется способ, сильно облегчающий решение. Решив, изучить его подробнее, я выяснила, что этот метод известен уже около 50 лет и в разных источниках фигурирует под названиями «метод декомпозиции», «метод замены множителей», «обобщенный метод интервалов», «метод рационализации». В школьной программе он не изучается, но его применение значительно облегчает решение заданий ЕГЭ задания №15, в частности логарифмических, показательных неравенств.
Цель исследовательской работы:
Изучение теоретического обоснования метода рационализации.
Задачи:
1. Изучить теоремы, которые позволяют заменять сложные выражения на более простые;
2. Рассмотреть примеры применения метода рационализации при решении логарифмических, показательных неравенств;
3. Найти примеры неравенств, которые могут быть решены методом рационализации.
Актуальность работы заключается в том, что данный метод позволяет успешно решать логарифмические и показательные неравенства задания №15 ЕГЭ по математике.
Здесь будет выводиться история переписки.
В основе методов решения рациональных неравенств лежит очевидный факт: непрерывная функция на отрезке между двумя нулевыми значениями не изменяет знак (положительна или отрицательна). Некоторые элементарные свойства многочленов, связанные с понятием кратного корня, позволяют быстро установить знак дробно-рациональной функции на каждом таком интервале монотонности. Заметим, что в общем случае требуется вычислять значения функции в «пробных» точках на каждом интервале, что более трудоемко.
Я рассмотрю примеры логарифмических и показательных неравенств, у которых основание, выражение под знаком логарифма, степень – многочлены. Оказывается, такие неравенства эффективно сводятся к дробно-рациональным или рациональным, причем (что важно, например, на ЕГЭ) полученные решения будут более компактными по сравнению с традиционными.
II. Сведение логарифмического неравенства к системе рациональных неравенств
Рассмотрим логарифмическое неравенство вида
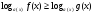 , (1)
, (1)
где 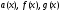 - некоторые функции.
- некоторые функции.
Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства.
В первом случае, когда основания логарифмов удовлетворяют условию
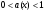 , знак неравенства меняется:
, знак неравенства меняется: 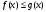 .
.
Во втором случае, когда основание удовлетворяет условию 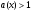 , знак неравенства сохраняется:
, знак неравенства сохраняется: 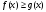 .
.
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь объединить, рационализировать?
Ответ на этот вопрос содержится в следующей теореме.
Теорема 1. Логарифмическое неравенство
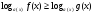
равносильно следующей системе неравенств:
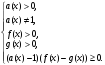 (2)
(2)
Доказательство. Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство. Если 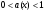 , то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство
, то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство 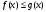 . Если же
. Если же 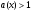 , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство
, то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство 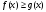 . Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана.
. Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана.
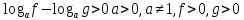
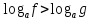
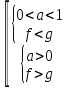
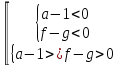

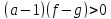
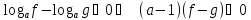
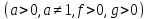
Частные случаи:
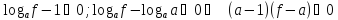
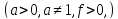
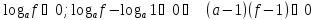
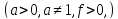

-
-
, h
III. Сведение показательного неравенства к системе рациональных неравенств
Теперь рассмотрим показательное неравенство вида
 (3)
(3)
Так же, как в предыдущем пункте, 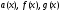 - некоторые функции.
- некоторые функции.
И снова вспомним, что традиционное решение такого неравенства приводит к двум случаям. В первом основание степени положительно, но меньше единицы (знак неравенства меняется), во втором случае основание степени больше единицы (знак неравенства сохраняется).
Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.
Теорема 2. Показательное неравенство

равносильно следующей системе неравенств:
(4)
Нетрудно заметить, что система (4) аналогична системе (2) из теоремы 1 (правда, в ней нет требования положительности степеней). Доказательство теоремы 2 легко получить теми же рассуждениями, что и в теореме 1.


IV. Примеры решения неравенств методом рационализации
1.Решите неравенство:
Ответ: 
2.Решите неравенство:



-5 -1


 + - +
+ - +

Ответ: 
2.Решите неравенство:
 0
0 




 -_ + -_ + х
-_ + -_ + х

Ответ: 
Заключение
В ходе проделанной работы мне удалось изучить нестандартные методы решения сложных логарифмических и показательных неравенств. Это: равносильные переходы и обобщённый метод интервалов, метод рационализации, нестандартная подстановка, задания с ловушками на ОДЗ. В школьной программе эти методы отсутствуют.
Литература.
Дорофеев Г.В. Обобщение метода интервалов. Математика в школе.1989г, №3.
Яковлев И.В. Материалы по математике. MathUs.ru
Интернет-ресурсы, сайт «Решу ЕГЭ».
Корянов А.Г., Прокофьев А.А. Интернет – ресурс: http://alexlarin.net/ege/2017/
ЕГЭ-2017: Математика: самое полное издание типовых вариантов / авт.-сост. И.В. Ященко, И.Р. Высоцкий; под ред. А.Л. Семенова, И.В. Ященко. – М.: АСТ: Астрель, 2016. -123 с. – (Федеральный институт педагогических измерений).
Экзаменационные задания: http://alexlarin.net







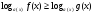 , (1)
, (1)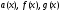 - некоторые функции.
- некоторые функции.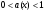 , знак неравенства меняется:
, знак неравенства меняется: 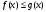 .
.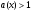 , знак неравенства сохраняется:
, знак неравенства сохраняется: 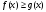 .
.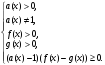 (2)
(2)