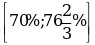Изучение понятия «концентрация».
Перед тем, как приступить к изучению различных способов решения задач на смеси, сплавы- рассмотрим некоторые основные допущения:
- все получающиеся сплавы или смеси однородны.
-при решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов, что отражает закон сохранения массы.
Определение. Процентным содержанием (концентрацией) вещества в смеси
называется отношение его массы к общей массе всей смеси.
Это отношение может быть выражено либо в дробях, либо в процентах. Например, если мы в 120 г воды добавим 30 г поваренной соли , то общая масса раствора станет 150 г, а концентрация соли в растворе 30:150= 0,2 - дробью или 20%. Оба ответа приемлемы.
Иногда концентрация может быть определена и по объёму. Например, если в смеси из 20 куб.м находится 5 куб.м вещества «а», то его объёмная концентрация равна 5:20=0,25 – в дробях или 25%. Но, как показывает практика, не всегда сумма объёмов смешиваемых веществ равна объёму их смеси. Поэтому чаще всего мы будем находить процентное содержание по массе.
Концентрация – это безразмерная величина. Сумма массовых долей всех компонентов, составляющих смесь, очевидно, равна единице.
Этапы решения задач:
Для начала определим, что такое задача:
-
Задача – это требование или вопрос, на который надо найти ответ, опираясь или учитывая те условия, которые в ней указаны.
-
Любая задача состоит из трёх частей: условие, объект, требование (вопрос) задачи.
-
Приступая к решению какой-либо задачи, надо её внимательно изучить, установить, в чем состоят её требования, каковы условия, исходя из которых надо её решать. Всё это называется - анализом задачи.
Весь процесс решения задачи можно разделить на восемь этапов:
1-й этап: анализ
2-й этап: схематическая запись
3-й этап: поиск способа решения
4-й этап: осуществление решения
5-й этап: проверка решения
6-й этап: исследование задачи
7-й этап: формулировка ответа
8-й этап: анализ решения.
Но чтобы решить задачу, нужно определить её вид и тип. По отношению к теории существует два вида задач: стандартные и нестандартные.
Сначала рассмотрим стандартный вид. Это задачи, для которых имеются общие правила и положения, определяющие точную программу их решения. Сам процесс решения имеет следующие особенности:
-
Анализ сводится к установлению вида, к которому относится задача.
-
Поиск решения состоит в составлении последовательности шагов решения задач этого вида.
-
Само решение стандартной задачи состоит в применении этой общей программы к её условиям.
Но всё-таки, чтобы правильно решать такие задачи, в первую очередь надо определить её вид.
Теперь рассмотрим нестандартные задачи. Исходя из определения стандартных задач, для них не имеется общих правил и положений. Процесс решения любой нестандартной задачи состоит в последовательном применении двух основных операций:
1) переформулировка нестандартной задачи к другой, ей эквивалентной, но уже стандартной.
2) разбиение нестандартной задачи на несколько стандартных подзадач.
Подробнее рассмотрим задачи на смеси и сплавы.
Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты.
Задача 1. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Изобразим каждый из сплавов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Кроме того, на модели отобразим характер операции – сплавление, поставим знак «+» между первым и вторым прямоугольниками. Поставив знак «=» между вторым и третьим прямоугольниками, мы тем самым показываем, что третий сплав получен в
результате сплавления первых двух. Полученная схема имеет следующий вид:

Теперь заполняем получившиеся прямоугольники в соответствии с условием задачи:
-
Над каждым прямоугольником («маленьким») указываем соответствующие компоненты сплава. При этом обычно бывает достаточно использовать первые буквы их названия (если они различны). Удобно сохранять порядок соответствующих букв.
-
Внутри прямоугольников вписываем процентное содержание (или часть) соответствующего компонента. Понятно, что если сплав состоит из двух компонентов, то достаточно указать процентное содержание одного из них.
-
В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.
-
Под прямоугольником записываем массу (или объем) соответствующего сплава (или компонента).
Рассматриваемый в задаче процесс можно представить в виде следующей модели- схемы:






медь
свинец
медь
свинец
свинец
медь











65%
=
+
30%
15%


200г
Решение.
1-й способ. Пусть хг – масса первого сплава. Тогда, (200-х)г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:

Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):
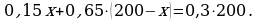
Решив это уравнение, получаем х=140. При этом значении х выражение 200-х=60. Это означает, что первого сплава надо взять140г, а второго-60г.
Ответ:140г. 60г.
2-й способ. Пусть х г и у г – масса соответственно первого и второго сплавов, то есть пусть исходная схема имеет вид:
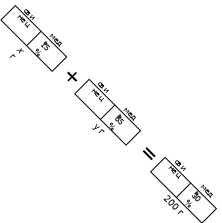
Легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:
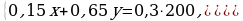
Решение системы приводит к результату: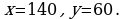 Значит, первого сплава надо взять 140 г, а второго-60 г.
Значит, первого сплава надо взять 140 г, а второго-60 г.
Ответ: 140г,60г.
Задача 2. В 4кг сплава меди и олова содержится 40% олова. Сколько килограммов олова надо добавить к этому сплаву, чтобы его процентное содержание в новом сплаве стало равным 70%?
Решение: Пусть х кг – искомое количество олова. Тогда масса полученного
сплава равна ( 4+х) кг. Составим схему и внесем эти выражения на схему:
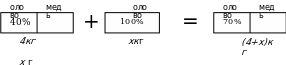
Составим уравнение, подсчитав массу олова слева и справа от знака равенства на схеме. Получаем уравнение: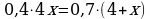 (1), корнем которого служит
(1), корнем которого служит 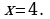
Отметим, что уравнение можно составить и на основе подсчета массы меди слева и справа от знака равенства. Для этого понадобится знать процентное содержание меди в данном и полученном сплавах. Внесем эти данные в схему:

В этом случае получаем следующее уравнение:
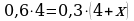 (2).
(2).
Уравнение (1) равносильно уравнению (2). В этом легко убедиться, решив последнее уравнение. Его корень равен 4. Обычно решают то уравнение, которое проще. В нашем случае разница не так заметна. Вместе с тем, второе уравнение содержит переменную только в одной (правой) части, и его обе части сразу можно разделить на 0,3. Поэтому предпочтение можно отдать второму уравнению.
Ответ:4кг.
Задача 3. К некоторому количеству сплава меди с цинком, в котором эти металлы находятся в отношении 2:3, добавили 4 кг чистой меди. В результате получили новый сплав, в котором медь и цинк относятся как 2:1. Сколько килограмм нового сплава получилось?
Решение.
Прежде чем составлять схему, уточним, что в первом сплаве медь составляет 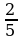 , а в полученном сплаве -
, а в полученном сплаве - 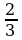 . Обозначим массу полученного сплава х кг, и, внеся указанные части в соответствующие фрагменты схемы, получаем:
. Обозначим массу полученного сплава х кг, и, внеся указанные части в соответствующие фрагменты схемы, получаем:
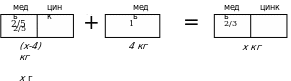
Нетрудно составить уравнение, подсчитав количество меди слева от знака
неравенства, и приравняв его к количеству меди, справа от него. Получаем
уравнение: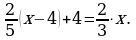 Решив его, получаем искомое значение: х=9.
Решив его, получаем искомое значение: х=9.
Замечание. Можно было составить уравнение на основе подсчета массы
цинка в обеих частях неравенства. Для этого внесем в схему необходимые данные:
1)если в первом сплаве медь составляет часть 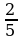 , то цинк –
, то цинк – 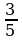 ;
;
 2) если в полученном сплаве медь составляет часть
2) если в полученном сплаве медь составляет часть 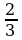 , то цинк –
, то цинк – 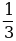 .
.
Уравнение в этом случае имеет вид: 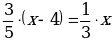 Это уравнение равносильно предыдущему.
Это уравнение равносильно предыдущему.
Ответ х=9кг.
Задача 4. Имеются три смеси, составленные из трех элементовA, B и С. В первую смесь входят только элементы А и В в весовом отношении 1:2, во вторую смесь входят только элементы В и С в весовом отношении 1:3, в третью смесь входят только элементы А и С в весовом отношении 2:1. В каком отношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в весовом отношении 11:3:8?
Решение.
Предшествующая работа позволяет школьникам без проблем составить одну из схем, где за х единиц веса, у единиц веса и z единиц веса обозначены соответственно вес первой, второй и третьей смеси.
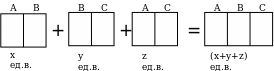
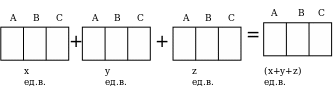 Вторая схема может иметь вид:
Вторая схема может иметь вид:
Подсчет и уравнивание веса любых двух из трех компонентов рассматриваемых смесей приводит к системе двух уравнений с тремя переменными. Если рассмотрим компоненты А и В, то система имеет вид:
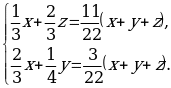

Решение этой системы может вызвать затруднения у школьников: количество уравнений (их два) меньше числа переменных (их три). Навести на решение поможет правило: составить выражение, значение которого надо найти по вопросу задачи. Это выражение имеет вид: x:y:z. Значит, для ответа на вопрос задачи совсем не обязательно находить значение каждой из переменных. Достаточно найти два отношения x:y и y:z или x:y и z:y. Для нахождения двух последних отношений разделим левую и правую части каждого уравнения на у (у≠0).Получаем систему:
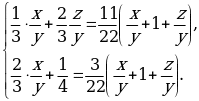
Теперь система имеет два уравнения и две переменных: 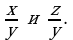 Целесообразно для удобства записей ввести новые переменные:
Целесообразно для удобства записей ввести новые переменные: 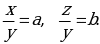 Теперь система принимает вид:
Теперь система принимает вид:
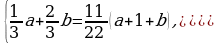
В результате решения системы получаем: 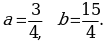 это означает,
это означает,
что 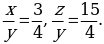 следовательно, искомое отношение имеет вид: x:y:z=3:4:15.
следовательно, искомое отношение имеет вид: x:y:z=3:4:15.
Ответ:3:4:15.
Задача 5. Имеется два сплава золота и серебра: в одном массы этих металлов находятся в отношении 2:3, а в другом – в отношении 3:7. Сколько килограммов нужно взять от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро находились бы в отношении 5:11?
Решение:
Золото серебро Золото серебро золото серебро

Х кг ( 8-х) кг 8 кг
Условно разделим сплав на золото и серебро.
Пусть х кг масса куска, взятого от первого сплава. Тогда масса куска, взятого от
второго сплава (8 – х) кг.
Масса золота в первом куске 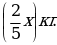
Масса золота во втором куске 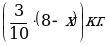
Масса золота в новом сплаве 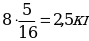
Получим уравнение
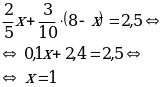
1 кг нужно взять от первого сплава.
8 – 1 = 7 (кг) – от второго сплава.
Ответ: 1кг; 7 кг.
Задача 6. Имеются два слитка сплава серебра и олова. Первый слиток содержит 360г серебра и 40г олова, а второй слиток – 450г серебра и 150г олова. От каждого слитка взяли по куску, сплавили их и получили 200г сплава, в котором оказалось 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка.
Решение:
Серебро олово серебро олово серебро олово

Х 200-х 200
Первый слиток имеет вес 400 г, второй – 600 г.
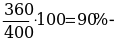 серебра в первом слитке (соответственно и в первом куске).
серебра в первом слитке (соответственно и в первом куске).
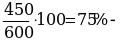 серебра во втором слитке (соответственно и во втором куске).
серебра во втором слитке (соответственно и во втором куске).
Пусть х г масса куска, взятого от первого слитка, а (200-х)г – от второго.
0,9х (г) – серебра в первом куске;
0,75(200-х) (г)- серебра во втором, тогда получим уравнение
0,9х +0,75(200-х)=0,81*200
0,9х+150-0,75х=162
0,15х=12
Х=80г от первого куска, тогда 200-80=120 г от второго.
Ответ: 120 грамм.
Задача 7. Для консервирования 10 кг баклажан необходимо 0,5 л столового уксуса (10 % раствор уксусной кислоты). У хозяйки имеется уксусная эссенция (80 % раствор уксусной кислоты), из которой она готовит уксус, добавляя в нее воду. Сколько миллилитров уксусной эссенции понадобится хозяйке для консервирования 20 кг баклажан?
Решение.
Для консервирования 20кг баклажан понадобится 1л или 1000мл столового уксуса (10% раствор уксусной кислоты). Для получения его из х мл уксусной
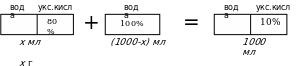 эссенции (80% раствор уксусной кислоты) необходимо добавить воду, тогда схема для решения задачи имеет вид:
эссенции (80% раствор уксусной кислоты) необходимо добавить воду, тогда схема для решения задачи имеет вид:
Составим уравнение, подсчитав количество уксусной кислоты слева от знака неравенства, и приравняем его к количеству уксусной кислоты справа от него. Получаем уравнение 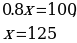
Значит, для приготовления 500мл маринада понадобится 125мл уксусной эссенции (80% раствор уксусной кислоты).
Ответ:125мл.
Задача 8. Свежие абрикосы содержат 80 % воды по массе, а курага (сухие
абрикосы) – 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?
Решение.
При высыхании абрикос испаряется вода, количество сухого вещества не меняется. Схема для решения такой задачи имеет вид:
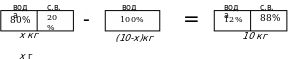
Составим уравнение, подсчитав количество сухого вещества в левой и правой части схемы:
0,2х=8,8
х=44.
Ответ:44кг.
Задача 9. Влажность сухой цементной смеси на складе
составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
Вода с.в вода вода с.в

400 кг х кг
Решение:
400*0,82= 0,8*х
328=0,8х
Х=410 кг
Ответ: 410 кг.
Анкетирование
В ходе научного исследования мной было проведено анкетирование учащихся 9-11 классов МБОУ «Гимназия №25» . Всего опрошено 92 человека. Всем предлагалось ответить на следующие вопросы:
1.Вызывают ли у Вас затруднения решение задач на концентрацию и совместную работу?
2.Знаете ли Вы способы решения данных задач?
Цель данного опроса:
Узнать степень подготовки учащихся по теме: «Решение текстовых задач на концентрацию, смеси, сплавы».
Результаты анкетирования:
- Все участники опроса испытывают затруднения при рассмотрении решений задач данного типа;
- Лишь 33 % из 92 опрошенных ознакомлены со способами решения данных задач.
Проанализировав результаты анкетирования, я пришла к выводу, что большая часть учащихся 9-11 класса, а именно 67 %, не может решать задачи на концентрацию , смеси и сплавы, и поэтому при встрече таких задач на ЕГЭ они могут потерять драгоценные для себя балы. По этой причине были проведены несколько ознакомительных занятий в 9-11х классах по теме: «Решение текстовых задач части «В» на ЕГЭ на концентрацию, смеси и сплавы». На данных занятиях учащимся были предложены задачи по этой теме, с помощью которых мной были раскрыты основные понятия, встречающиеся в задачах, и представлены основные формулы, необходимые для их решения, был проиллюстрирован общий алгоритм решения, а также наиболее наглядный и удобный способ записи условий таких задач.
Анкетирование учащихся-выпускников (Сентябрь 2012г).
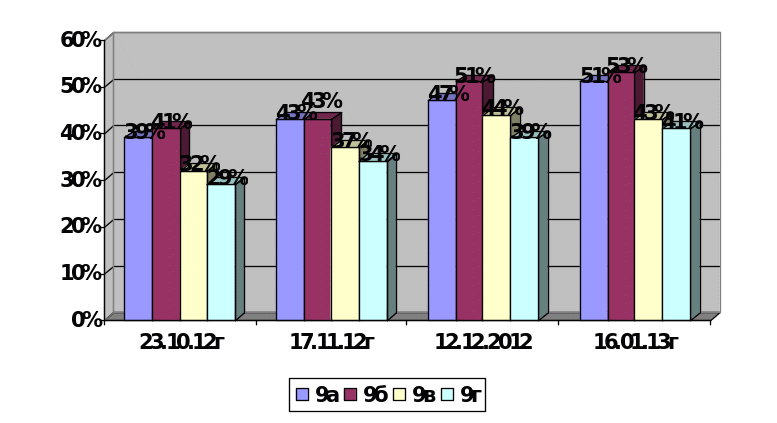
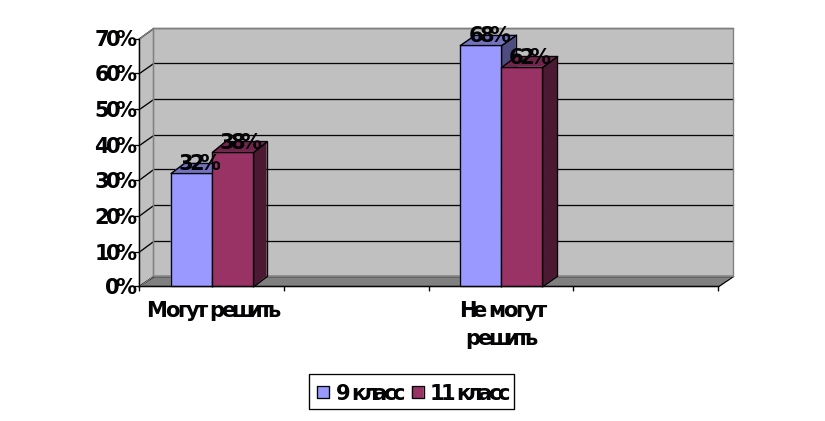 Итоги тестирования учащихся 9-х классов в октябре-декабре 2012 и январь 2013 г по теме: «Задачи на смеси, сплавы»
Итоги тестирования учащихся 9-х классов в октябре-декабре 2012 и январь 2013 г по теме: «Задачи на смеси, сплавы»
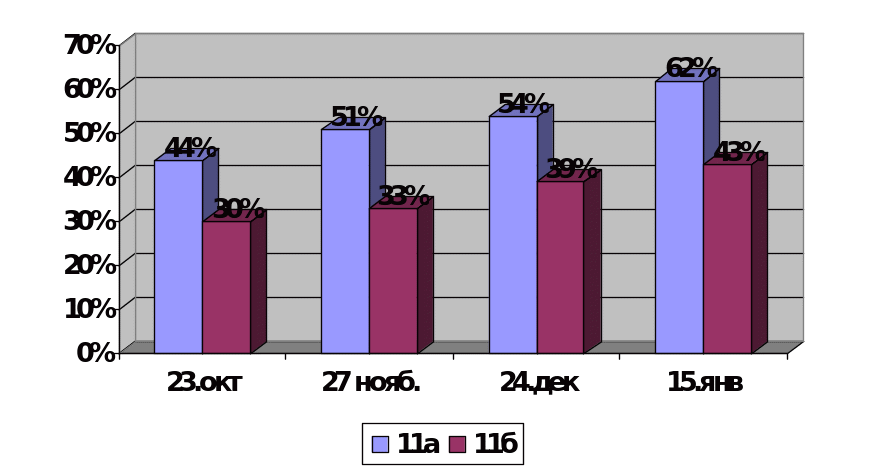
Итоги тестирования учащихся 11-х классов в октябре-декабре 2012 и январь 2013 г по теме: «Задачи на смеси, сплавы»
Выводы
В ходе научного исследования мной были решены следующие цели и задачи:
1.Ознакомила учащихся со способами решений задач;
2.Провела выборочный анкетный опрос среди учащихся «Гимназия №25»;
3.Рассмотрела методы решения задач на смеси и сплавы ;
4.Выработала следующий алгоритм решения задач на смеси и сплавы:
1.Изучить условия задачи.
2.Выбрать неизвестные величины (их обозначают буквами х, у и т.д.), относительно которых составить уравнение или систему уравнений, этим, мы создаем математическую модель ситуации, описанной в условии задачи.
3.Используя условия задачи, определить все взаимосвязи между данными величинами.
4.Составить математическую модель задачи и решить ее.
5.Изучить полученное решение, провести критический анализ результата.
Таким образом, данная научная работа имеет практическое значение, так как может служить одним из способом решения задач на смеси и сплавы при подготовке к сдаче экзаменов.
Список литературы:
1.Галицкий М.Л Сборник задач по алгебре
2.Говоров В.М. Сборник задач для поступающих в вузы
3.Сикарский К.П. дополнительные главы по курсу математики.
4.Шабунин М.И. Математика для поступающих в Вузы
5.Шарыгин И.Ф. Решение задач. Факультативный курс по математики.
6. uztest.ru(сайт для подготовки к ЕГЭ)
7..Типовые тестовые задания/ Под ред. А. Л. Семенова, И. В. Ященко – Москва: Экзамен, 2012.
8. Алгебра 7класс. В двух частях.
Часть 1:Учебник для общеобразовательных учреждений.
Часть 2:Задачник для общеобразовательных учреждений.
Авторы: А.Г.Мордкович, Т.Н Мишустина, Е.Е.Тульчинская. М.Мнемозина, 2008год.
9. Алгебра 8класс. В двух частях.
Часть 1:Учебник для общеобразовательных учреждений.
Часть 2:Задачник для общеобразовательных учреждений.
Авторы: А.Г.Мордкович, Т.Н Мишустина, Е.Е.Тульчинская. М.:Мнемозина, 2008год.
10. Часть 1 Алгебра. Углубленное изучение. 8 класс.Учебник.
Автор: А.Г. Мордкович М.:Мнемозина, 2006год.
Часть 2 Алгебра. Углубленное изучение. 8 класс Задачник к учебнику А.Г.Мордковича.
Авторы: Л.И.Звавич, А.Р.Рязановский М.:Мнемозина, 2006год.
11. Алгебра 9 класс. В двух частях. Часть 1:Учебник для общеобразовательных
учреждений
Часть 2:Задачник для общеобразовательных учреждений.
Список Интернет ресурсов:
1."http://festival.1september.ru/"http://festival.1september.ru
2. "http://schoolmathematics.ru/"http://schoolmathematics.ru
3. "http://uztest.ru/"http://uztest.ru
http://www.alhimikov.net
4. "http://www.integral.edusite.ru/"http://www.integral.edusite.ru
ПРИЛОЖЕНИЕ.
-
Бронза – сплав меди и олова. В древности из бронзы отливали колокола, если в ней содержалось 75% меди. К куску бронзы 500кг и содержащему 72% добавили некоторое количество бронзы, содержащей 80% меди и получили бронзу, необходимую для изготовления колокола. Определите сколько добавили 80% бронзы.
Ответ:300кг.
-
В лаборатории изготовили 1кг 16% солевого раствора. Через неделю из этого раствора испарилось 200г воды. Какова стала концентрация соли в растворе?
Ответ:20%.
3.. Имеются два сплава, в одном из которых содержится 10%, а в другом – 20% меди. Сколько нужно взять первого и второго сплавов, чтобы получить 15 кг нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.
4.Имеется 600г сплава золота и серебра содержащего золото и серебро в отношении 1:5 соответственно. Сколько грамм золота необходимо добавить к этому сплаву чтобы получить новый сплав содержащий 50% серебра.
Ответ:400г.
5.Имелось два слитка меди. Процент содержания меди в первом слитке на 40% меньше, чем во втором. После того как оба слитка сплавили, получился слиток, содержащий 36% меди. Найдите процентное содержание меди в каждом слитке, если в первом было 6 кг меди, а во втором — 12 кг.
Ответ:20% и 60%
6. Сколько чистого спирта нужно добавить к 735 г 16%-ного раствора йода и спирта, чтобы получить 10%-ный раствор?
Ответ:441г.
7. Смешали 30%-ный раствор соляной кислоты с ее 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов 30 % -ного раствора было взято?
Ответ:150г.
-
Имеются два слитка, состоящие из цинка, меди и олова. Известно, что первый слиток массой 150 кг содержит 40% олова, а второй массой 250 кг — 26% меди. Процентное содержание цинка в обоих слитках одинаково. Сплавив первый и второй слитки, получили сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в полученном сплаве?
Ответ:170 кг.
9.Имеются два сплава, состоящие из меди, цинка и олова. Известно, что первый сплав содержит 25% цинка, а второй — 50% меди. Процентное содержание олова в первом сплаве в 2 раза меньше, чем во втором. Сплавив 200 кг первого сплава и 300 кг второго, получили новый сплав, в котором оказалось 28% цинка. Определите, сколько килограммов меди содержится в получившемся новом сплаве.
Ответ: 280 кг.
10. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра составляет 14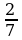 % веса меди. Сколько серебра в данном сплаве?
% веса меди. Сколько серебра в данном сплаве?
Ответ:0,25 кг.
11. Имелись два разных сплава меди, причем процент содержания меди в первом сплаве был на 40% меньше, чем во втором. После того как их сплавили вместе, получили сплав, содержащий 36% меди. Определите процентное содержание меди в обоих сплавах, если известно, что в первом ее 6 кг, а во втором — вдвое больше.
Ответ:20% и 60%.
12.Два раствора, первый из которых содержал 800 г, а второй 600 г безводной серной кислоты, смешали и получили 10 кг нового раствора серной кислоты. Определите массу первого и второго растворов, вошедших в смесь, если известно, что процент содержания безводной серной кислоты в первом растворе на 10% больше, чем во втором.
Ответ:4кг и 6 кг.
13.Свежие грибы по весу содержат 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 22 кг свежих?
Ответ:2,5 кг
14. Один сплав меди с оловом содержит эти металлы в отношении 2:3, другой — в отношении 3 : 7. В каком количестве надо взять эти сплавы, чтобы получить 12 кг нового сплава, в котором медь и олово были бы в
отношении 3:5?
Ответ: 9кг и 3кг.
15. 40% раствор серной кислоты разбавили 60% раствором, после чего добавили 5кг воды и получили раствор 20% концентрации. Если бы вместо 5кг воды добавили 5 кг 80% раствора серной кислоты, то получился бы 70% раствор. Сколько было 40% и 60% раствора серной кислоты?
Ответ: 1кг 40% и 2кг 60%..
16. В сосуд, содержащий 5 литров 12 процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация
получившегося раствора?
Ответ: 5%
17.Сколько литров воды нужно добавить в 2 л водного раствора, содержащего 60% кислоты, чтобы получить 20 процентный раствор кислоты?
Ответ: 4 л.
18. Смешали 4 литра 15 процентного водного раствора
с 6 литрами 25 процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Ответ: 21%
19. Сколько надо взять 5 процентного и 25 процентного раствора кислоты, чтобы получить 4 л 10 процентного раствора кислоты?
Ответ: 1 л, 3 л.
20. В сосуд емкостью 6л налито 4л 70% раствора серной
кислоты. Во второй сосуд той же емкости налито 3л 90% раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился 74% раствор серной кислоты? Найдите все допустимые значения процентного содержания раствора серной кислоты в 6л раствора в первом сосуде.
Ответ: 1; 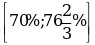
21. Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Ответ: 9 кг.
22. Имеется два сплава золота и серебра: в одном массы этих металлов находятся в отношении 2:3, а в другом – в
отношении 3:7. Сколько килограммов нужно взять от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро находились бы в
отношении 5:11?
Ответ: 1кг; 7 кг.
23. Имеется два сплава. Первый содержит 10% никеля, второй- 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Ответ: на 100 кг.
24. При смешивании 30 процентного раствора серной кислоты с10 процентным
раствором серной кислоты получилось 400 г 15 процентного раствора. Сколько граммов 30 процентного раствора было взято?.
Ответ:100 г.
25. Имеются два слитка сплава серебра и олова. Первый слиток содержит 360г серебра и 40г олова, а второй слиток – 450г серебра и 150г олова. От каждого слитка взяли по куску, сплавили их и получили 200г сплава, в котором оказалось 81% серебра. Определите массу (в граммах) куска, взятого от второго слитка.
Ответ: 120 г.
26. Первый раствор содержит 40% кислоты, а второй - 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 процентного раствора, то получился бы 70 процентный раствор. Сколько литров 60 процентного раствора кислоты было первоначально?
Ответ: 2 л.















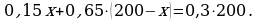

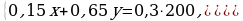
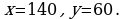 Значит, первого сплава надо взять 140 г, а второго-60 г.
Значит, первого сплава надо взять 140 г, а второго-60 г.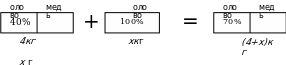
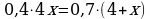 (1), корнем которого служит
(1), корнем которого служит 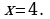

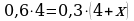 (2).
(2).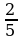 , а в полученном сплаве -
, а в полученном сплаве - 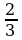 . Обозначим массу полученного сплава х кг, и, внеся указанные части в соответствующие фрагменты схемы, получаем:
. Обозначим массу полученного сплава х кг, и, внеся указанные части в соответствующие фрагменты схемы, получаем: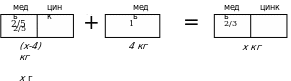
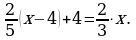 Решив его, получаем искомое значение: х=9.
Решив его, получаем искомое значение: х=9.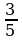 ;
; 2) если в полученном сплаве медь составляет часть
2) если в полученном сплаве медь составляет часть 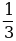 .
.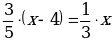 Это уравнение равносильно предыдущему.
Это уравнение равносильно предыдущему.
 Вторая схема может иметь вид:
Вторая схема может иметь вид: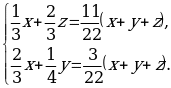

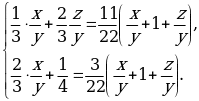
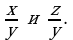 Целесообразно для удобства записей ввести новые переменные:
Целесообразно для удобства записей ввести новые переменные: 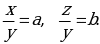 Теперь система принимает вид:
Теперь система принимает вид: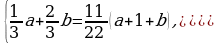
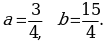 это означает,
это означает, 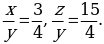 следовательно, искомое отношение имеет вид: x:y:z=3:4:15.
следовательно, искомое отношение имеет вид: x:y:z=3:4:15.
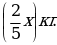
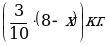
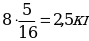
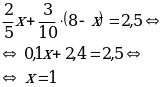

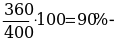 серебра в первом слитке (соответственно и в первом куске).
серебра в первом слитке (соответственно и в первом куске).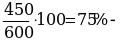 серебра во втором слитке (соответственно и во втором куске).
серебра во втором слитке (соответственно и во втором куске).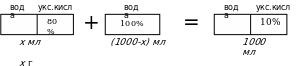 эссенции (80% раствор уксусной кислоты) необходимо добавить воду, тогда схема для решения задачи имеет вид:
эссенции (80% раствор уксусной кислоты) необходимо добавить воду, тогда схема для решения задачи имеет вид: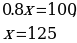
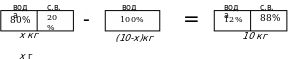

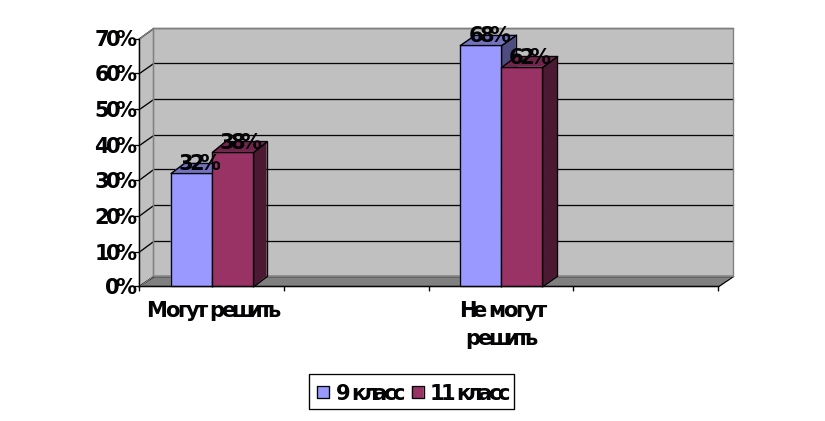 Итоги тестирования учащихся 9-х классов в октябре-декабре 2012 и январь 2013 г по теме: «Задачи на смеси, сплавы»
Итоги тестирования учащихся 9-х классов в октябре-декабре 2012 и январь 2013 г по теме: «Задачи на смеси, сплавы»
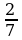 % веса меди. Сколько серебра в данном сплаве?
% веса меди. Сколько серебра в данном сплаве?