Методическая разработка курса
«ТРИГОНОМЕТРИЯ»
Программа курса:
1. Историческая справка.
2. Определение тригонометрических функций.
3. Свойства тригонометрических функций и их графики.
4. Квадранты единичной окружности. Знаки тригонометрических функций.
5. Вычисление значений тригонометрических функций без таблиц. Нахождение одних тригонометрических функций по значениям других.
6. Тождественные преобразования тригонометрических выражений.
7. Обратные тригонометрические функции и их графики.
8. Простейшие соотношения между обратными тригонометрическими функциями.
1. ВВЕДЕНИЕ
Слово "тригонометрия" составлено из греческих слов "тригонон" — треугольник и "метрезис" — измерение.
Тригонометрия — математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.
Углы произвольного треугольника нельзя связать непосредственно с его сторонами с помощью алгебраических соотношений. Поэтому тригонометрия вводит в рассмотрение, кроме самих углов, тригонометрические величины (синус, косинус, тангенс, котангенс). Эти величины уже можно связать со сторонами треугольника простыми
алгебраическими соотношениями. С другой стороны, по значению тригонометрической величины можно определить угол, и обратно. Правда, эти вычисления требуют длительных и утомительных расчетов, но эта работа проделана раз и навсегда и закреплена в таблицах.
Значение каждой тригонометрической величины изменяется с изменением угла, которому она соответствует; другими словами, тригонометрическая величина есть функция угла. Отсюда название тригонометрические функции.
Казалось бы, тригонометрию можно считать лишь частью геометрии, однако тригонометрические функции — это объект изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.
Основные формулы тригонометрии задаются теоремой синусов и теоремой косинусов.
Кроме них, часто применяется теорема тангенсов, открытая в XV в. немецким математиком И. Региомонтаном,
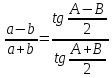
где a, b, с — стороны треугольника, а А, В, С — противоположные им углы, р — полупериметр треугольника.
Площадь треугольника помимо формулы Герона может быть выражена через стороны и тригонометрические величины углов еще несколькими способами:
 ,
, 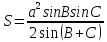 ,
, 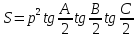 .
.
Тригонометрия возникла из практических нужд человека. С её помощью можно определить расстояние до недоступных предметов, существенно упрощать процесс геодезической съемки местности для составления географических карт.
Потребность в решении треугольников раньше всего возникла в астрономии, и в течение долгого времени тригонометрия развивалась как раздел астрономии.
Древнегреческие ученые разработали "тригонометрию хорд", изложенную Птолемеем (II в.). Он вывел соотношения, между хордами в круге, которые равносильны современным формулам для синуса половинного и двойного угла, синуса суммы и разности двух углов.
Дальнейший шаг в развитии тригонометрии сделали индийские ученые, которые заменили хорды синусами.
Общепринятые понятия тригонометрии сформулировались в процессе долгого исторического развития. Если, например, при введении основных понятий представляется естественным принимать радиус тригонометрического круга равным единице, то эта простая идея появилась только в X - XI вв.
Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры).
Буквенные обозначения утвердились в тригонометрии лишь в середине XVIII в. благодаря Л. Эйлеру Этот великий математик придал всей тригонометрии ее современный вид. Величины sin x, cos x и т.д. он рассматривал как функции числа х — радианной меры соответствующего угла. Эйлер давал числу х всевозможные значения: положительные, отрицательные, комплексные. Он ввел и обратные тригонометрические
функции.
2. Углы и их измерение
Определение 2.1. Угол — это часть плоскости, ограниченная двумя
лучами, выходящими из одной точки, вершины угла.
Угол разбивает плоскость на две части. Каждая из них называется плоским углом.
Плоские углы с общими сторонами называются дополнительными.
В качестве единицы измерения углов принят градус — 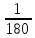 часть развернутого угла (прямой).
часть развернутого угла (прямой).
Зафиксируем не только вершину угла, но и один из образующих его лучей. Поместим вершину yгла в начало координат, а одну сторону направим по оси ОХ
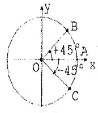
Проведем окружность с центром в О (рис.1). Радиус ОА называется начальным радиусом.
Если повернуть начальный радиус против часовой стрелки, то угол поворота — положительный; если повернуть по часовой стрелке, то угол поворота отрицательный.
На рис.1 начальный радиус перешел в ОВ, угол поворота положительный и равен 45°,
и начальный радиус перешел в ОС — угол поворота отрицательный и равен (–45°).
Наряду с градусной мерой угла употребляется радианная мера угла.
Из геометрии известна следующая теорема.
Теорема 2.1. Отношение длины окружности к ее диаметру не
зависит от окружности, т.е. одно и то же для любых окружностей.
Отношение длины окружности (l) к диаметру (2R) принято обозначать греческой буквой π: 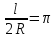 .
.
Число π — иррациональное.
Приближенное значение π ≈ 3,1416.
Длина окружности вычисляется по формуле 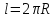 .
.
Определение 2.2. Центральным углом в окружности называется плоский угол с. вершиной в ее центре.
Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (рис.2)
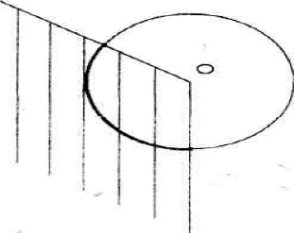
Рис.2
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Развернутому углу (прямой) соответствует длина полуокружности πR.
Углу в 1° соответствует дуга 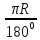 . Углу в п° соответствует дуга
. Углу в п° соответствует дуга 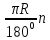 .
.
Определение 2.3. Радианной мерой утла называется отношение длины соответствующей дуги к радиусу окружности, т.е.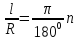 .
.
Радианная мера угла получается из градусной умножением на 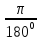 .
.
В частности, радианная мера угла 180° равна π.
ПРИМЕР 2.1. Найти площадь сектора радиуса 10см, если дуга сектора содержит 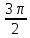 радиан.
радиан.
Решение. Площадь круга равна π R², где R — радиус круга.
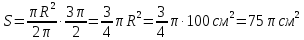
3. Тригонометрические функции острого угла
Решение всяких треугольников в конечном счете сводится к решению прямоугольных треугольников. В прямоугольном треугольнике отношение двух сторон не зависит от длин, а полностью зависит от величины одного из углов.
Теорема 3.1. Отношение сторон прямоугольного треугольника зависит только от градусной меры угла.
Доказательство. Пусть ABC и А'В'С' — два прямоугольных треугольника с одним и тем же углом а при вершинах А и А'.
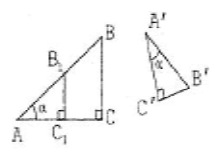 Рис. 3
Рис. 3
Требуется доказать, что 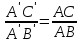 ,
, 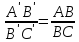 и т.д.
и т.д.
Отложим на луче АВ отрезок 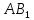 , равный А'В', на луч АС — отрезок
, равный А'В', на луч АС — отрезок 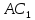 , равный А'С'.
, равный А'С'.
Треугольники 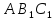 и А'В'С' равны по первому признаку. Поэтому угол
и А'В'С' равны по первому признаку. Поэтому угол 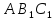 прямой, Значит, прямые
прямой, Значит, прямые  и ВС, перпендикулярные прямой АС, параллельны.
и ВС, перпендикулярные прямой АС, параллельны.
По обобщенной теореме Фалеса: 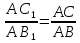 , а так как
, а так как 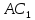 = А'С',
= А'С', 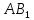 = А'В', то
= А'В', то
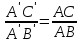 .
.
Аналогично 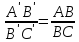 , что и требовалось доказать
, что и требовалось доказать
Отношения различных пар сторон в прямоугольном треугольнике называются тригонометрическими функциями его острого угла (рис. 4).
1. Синус угла А — это отношение противолежащего катета к гипотенузе, т.е.
sin A =  .
.
2. Косинус угла А — это отношение прилежащего катета к гипотенузе, т.е.
cos A =  .
.
3. Тангенс угла А — это отношение противолежащего катета к прилежащему, т.е.
tgA =  .
.
4. Котангенс угла А — это отношение прилежащего катета к противолежащему, т.е. ctgA =  .
.
5. Секанс угла А — отношение гипотенузы к прилежащему катету, т.е.
sec A =  .
.
6. Косеканс угла А — отношение гипотенузы к противолежащему катету, т.е.
cosecA =  .
.
По отношению к углу В названия меняются: sin B =  ,cos B =
,cos B =  , tgB =
, tgB =  , ctgB =
, ctgB =  и.т.д.
и.т.д.
Для некоторых углом можно найти точные выражения их тригонометрических величин. Занесем их в таблицу.
Таблица 1
4. Основные соотношения между тригонометрическими функциями одного и того же угла
Из определения синуса, косинуса, тангенса, котангенса и теоремы Пифагора следуют основные тождества:
Пример 4.1. Вычислить sin 18°.
Рассмотрим равнобедренный треугольник ABC с углом при вершине 36°. Тогда углы при основании но 72°.
Проведем биссектрисы углов А и В, обозначив их AM и ВК.
Треугольники ABC и MAC подобны по трем углам.
Пусть АВ = ВС = а, АС = b, обозначим МС = х, ВМ = а – х.
Тогда из подобия треугольников следует  (1). Так как биссектриса {AM) внутреннего угла треугольника делит сторону (ВС) которую она пересекает, на отрезки, пропорциональные прилежащим сторонам, то имеем
(1). Так как биссектриса {AM) внутреннего угла треугольника делит сторону (ВС) которую она пересекает, на отрезки, пропорциональные прилежащим сторонам, то имеем  . (2)
. (2)
ВК — является высотой треугольника ABC. Тогда ВКС прямоугольный, а угол КВС = 18°. sin 18°=  .
.
Итак, из (1) и (2) надо найти  .
.
Из (1) получаем  , подставим в (2)
, подставим в (2)
 или
или  .
.
Обозначим  , получаем
, получаем  ,
,  , откудa
, откудa  . Так как по геометрическому смыслу
. Так как по геометрическому смыслу , то выбираем
, то выбираем  .
.
Отсюда sin 18° =  .
.
Используя основные формулы, можно найти cos 18°, tg l8°, ctg 18°.
Пример 4.2. Доказать тождество:
.
Решение. Тождество будет доказано, если установить, что разность между выражениями, стоящими в левой и правой частях этого тождества, равна нулю.
3







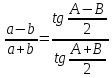
 ,
, 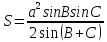 ,
, 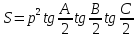 .
.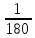 часть развернутого угла (прямой).
часть развернутого угла (прямой).
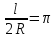 .
.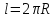 .
.
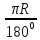 . Углу в п° соответствует дуга
. Углу в п° соответствует дуга 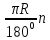 .
.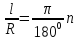 .
.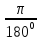 .
.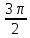 радиан.
радиан.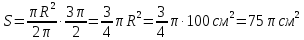
 Рис. 3
Рис. 3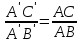 ,
, 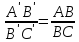 и т.д.
и т.д.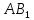 , равный А'В', на луч АС — отрезок
, равный А'В', на луч АС — отрезок 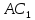 , равный А'С'.
, равный А'С'.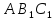 и А'В'С' равны по первому признаку. Поэтому угол
и А'В'С' равны по первому признаку. Поэтому угол  и ВС, перпендикулярные прямой АС, параллельны.
и ВС, перпендикулярные прямой АС, параллельны.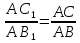 , а так как
, а так как 




















