Методическая разработка урока "Движение по воде. Решение задач."

?

1

.

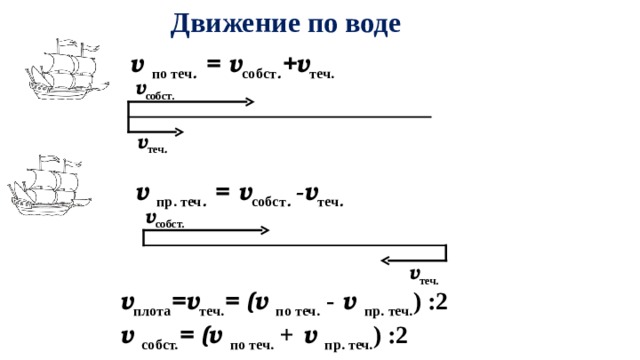
Движение по воде

v по теч . = v соб c т . + v теч.

v собст.

v теч .

v пр. теч . = v собст . - v теч .

v собст.

v теч.

v плота = v теч. = ( v по теч. - v пр. теч. ) :2

v собст. = ( v по теч. + v пр. теч. ) :2

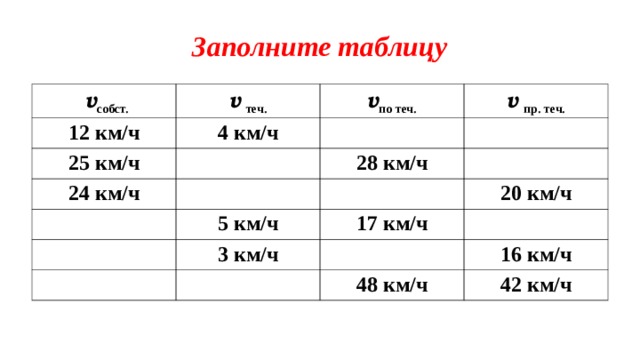
Заполните таблицу

v собст.

v теч.

12 км/ч

v по теч.

4 км/ч

25 км/ч

24 км/ч

v пр. теч.

28 км/ч

5 км/ч

20 км/ч

17 км/ч

3 км/ч

16 км/ч

48 км/ч

42 км/ч

Заполните таблицу

v собст.

v теч.

12 км/ч

v по теч.

4 км/ч

25 км/ч

24 км/ч

v пр. теч.

16 км/ч

3 км/ч

12 км/ч

4 км/ч

28 км/ч

8 км/ч

22 км/ч

28 км/ч

5 км/ч

19 км/ч

20 км/ч

17 км/ч

3 км/ч

45 км/ч

7 км/ч

21км/ч

3 км/ч

16 км/ч

48 км/ч

42 км/ч

Задача 1

На путь по течению реки катер затратил 3 часа, а на обратный путь 4,5 часа. Какова скорость течения реки, если скорость катера относительно воды 25 км/ч?

Решение(1 способ): п усть v теч. = x , согласно условию задачи заполним

v соб = 25 км/ч

v соб = 25км/ч

v теч

таблицу. Составим уравнение:

3(25+ х )=4,5(25- х );

7,5 х =37,5;

х= 5

Ответ: 5 км/ч

v (км/ч)

По течению

25+ х

t (ч)

Против течения

S( км)

3

25- х

3(25+ х )

4,5

4,5(25- х )

3 ч

4,5 ч

Глава III , 9 класс. 9.2 Физика . Задача 9. 2 . 1

Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с.

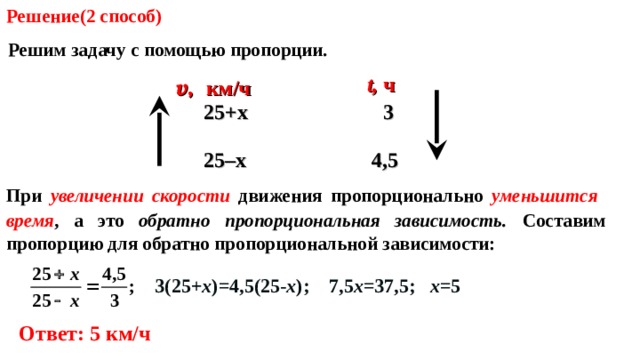
Решение( 2 способ)

Решим задачу с помощью пропорции.

v , км/ч

t, ч

3

25+ х

4,5

25–x

При увеличении скорости движения пропорционально уменьшится время , а это обратно пропорциональная зависимость. Составим пропорцию для обратно пропорциональной зависимости:

3(25+ х )=4,5(25- х ); 7,5 х =37,5; х= 5

Глава III , 9 класс. 9.2 Физика Задача 9. 2 . 1

Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с.

Ответ: 5 км/ч

Задача 2 Теплоход плывёт из А в В двое суток, из В в А трое суток. Сколько суток плывет из А в В плот?

Решение: пусть S – путь из А в В, х – собственная скорость теплохо-

да, у – скорость течения реки, тогда S = ( х + у ) · 2 и S = ( х - у ) · 3 .

Составим уравнение:

2 х +2 у = 3 х -3 у ;

-х = -5 у ; х = 5 у;

Значит, S = 2 х +2 у = 2 · 5 у +2 у = 12 у , тогда суток.

Ответ: 12 суток

Задача 3 Лодка прошла по течению реки расстояние между двумя пристанями за 6 ч, а обратный путь она совершила за 8 ч. За сколько времени пройдет это расстояние плот, пущенный по течению реки?

Решение: пусть S - расстояние между двумя пристанями , х – собствен-

ная скорость лодки, у – скорость течения реки, тогда S = ( х + у ) · 6 и

S = ( х - у ) · 8 . Составим уравнение:

6 х +6 у = 8 х -8 у ;

2 х = 14 у ; х = 7 у;

Значит S = 6 х +6 у = 6 · 7 у +6 у = 48 у , тогда часов.

Ответ: 48 часов

Задача 5

Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?

Решение: пусть S км – расстояние до стоянки. Согласно усл6вию задачи скорость теплохода по течению равна 25+3=28 км/ч, против течения –

25-3=22 км/ч. В исходный пункт теплоход возвращается через 30 часов после отплытия из него. Составим уравнение.

22 S+28S-25∙28 ∙22=0 ;

50 S = 25∙28 ∙22 ; S= 28 ∙11=308 ; 308∙2=616 км- путь туда и обратно.

Ответ: 616 км

Задача 6

Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.

Решение: пусть х - скорость течения реки, согласно условию задачи

заполним таблицу.

v (км/ч)

По течению

11+ х

Против течения

S( км)

112

11- х

t (ч)

112

112(11-х)+6(11+х)(11-х)=112(11+х)

Задача 7

Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.

0 по условию Ответ: 16 км/ч " width="640"

Решение

Пусть х км/ч - скорость лодки в неподвижной воде, против течения скорость уменьшается на 1 км/ч, т.е. ( х- 1) км/ч - скорость против течения. По течению скорость увеличивается на 1 км/ч, т.е. ( х + 1) км/ч - скорость по течению. Составим таблицу.

Т.к. на обратный путь лодка затратила времени меньше на 2 часа, то получим уравнение:

v (км/ч)

По течению

х +1

Против течения

S (км)

х -1

255

t (ч)

255

255 х +255-255 х +255=2( х -1)( х +1) ;

2 х 2 – 512 = 0; х 1 =16, х 2 = - 16 х 0 по условию

Ответ: 16 км/ч

Задача 8 Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.

Решение: пусть х - собственная скорость лодки. Согласно условию задачи заполним таблицу. На весь путь лодка потратила 5 часов. Составим

уравнение.

v (км/ч)

По

течению

х +3

Против течения

S (км)

х - 3

t (ч)

36

36

х 1 =15 ; х 2 =-0,6 (посторонний корень)

Ответ: 15 км/ч

Задача 9 Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.

Решение:

Пусть х км/ч - собственная скорость лодки (в неподвижной воде), тогда ( х +4) км/ч – скорость лодки по течению реки, ( х- 4) км/ч – скорость лодки против течения реки.

ч – время движения лодки против течения реки, ч – время движения лодки по течению реки, что на 2 ч меньше времени против течения. Составим уравнение: 2( х 2 -16)=77( х +4)-77( х -4); х 2 =324;

х =-18 (посторонний корень)

Ответ: 18 КМ/Ч

Домашнее задание Решите задачи

1. Моторная лодка прошла путь от А до В по течению реки за 2,4 ч, а обратный путь за 4 ч. Найти скорость течения реки, если известно, что скорость лодки относительно воды 16 км/ч.

2. Катер прошел по течению реки 36 км и возвратилась обратно, затратив на весь путь 5 ч. Найдите скорость катера в стоячей воде, зная, что скорость течения равна 3 км/ч.

3. Моторная лодка и парусник, находясь на озере в 30 км друг от друга, движутся навстречу и встречаются через 1 ч. Если бы моторная лодка находилась в 20 км от парусника и догоняла его, то на это потребовалось бы 3 ч 20 мин. Определить скорости лодки и парусника, полагая, что они постоянны и неизменны в обоих случаях.∙