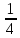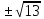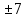Муниципальное бюджетное общеобразовательное учреждение
«Ликино-Дулевская гимназия»
Методическая разработка урока по алгебре в 8 классе:
«Решение квадратных уравнений»
Автор:
Барышникова Марина Александровна,
учитель математики преподаватель математики
2017 г.
Введение
Предмет: алгебра Класс - 8
Тема – «Решение квадратных уравнений»
Учебно-методическое обеспечение: Никольский С. М., Потапов М. К., Решетников Н.Н., Шевкин А. В. Алгебра 8. – М.: Просвещение, 2016.
Время реализации занятий – 45 минут
Оборудование и материалы для урока: компьютер, проектор, презентация для сопровождения урока, карточки-задания для учащихся.
Пояснительная записка
При решении многих задач на старшей ступени обучения, например, тригонометрических, показательных, логарифмических уравнений и неравенств, приходиться обращаться к нахождению корней квадратного трехчлена, области значений квадратичной функции, разложению трехчлена на множители, определению знака квадратного трехчлена.
В последнее время в материалах итоговой аттестации, ЕГЭ по математике и на вступительных экзаменах в высшие учебные заведения, предлагаются уравнения и неравенства второй степени. Урок предназначен для ликвидации пробелов в знаниях некоторых учащихся закрепление знаний и умений по данной теме.
Тема: «Решение квадратных уравнений», 8 класс
Тип урока: урок обобщения и систематизации знаний.
Цель урока: обобщить и систематизировать знания и умения по решению квадратных уравнений.
Задачи урока:
Образовательные: выработать умение выбирать рациональный способ решения квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
Развивающие: развивать логическое мышление, внимание, общеучебные умения;
Воспитательные: воспитывать интерес к математике, активность, мобильность, взаимопомощь, умение общаться.
План урока:
Организационный момент – 2 мин.
Устная работа – 5 мин.
Математическая разминка – 10 мин.
Математический диктант – 5 мин.
Физкультминутка – 3 мин.
Буквоград – 10 мин.
Повторение теоремы Виета – 3 мин.
Самостоятельная работа – 5 мин.
Подведение итогов – 2 мин.
Ход урока:
1.Организационный момент (2 мин.).
Цель нашего урока: обобщить и систематизировать знания и умения по решению квадратных уравнений.
Задачи урока:
Образовательные: выработать умение выбирать рациональный способ решения квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
Развивающие: развивать логическое мышление, внимание, общеучебные умения;
Воспитательные: воспитывать интерес к математике, активность, мобильность, взаимопомощь, умение общаться.
Сегодня на уроке мы систематизируем знания о методах решения квадратных уравнений, закрепим и усовершенствуем навыки решения квадратных уравнений.
2. Устная работа с классом (5 мин.).
На экране, записаны уравнения:
 +9x–12=0;
+9x–12=0;
4 +1=0;
+1=0;
 –2x+5=0;
–2x+5=0;
2 –5x+2=0;
–5x+2=0;
4 =1;
=1;
–2 –x+1=0;
–x+1=0;
 + 8x = 0;
+ 8x = 0;
2 =0;
=0;
– – 8x=1
– 8x=1
2x+ –1=0
–1=0
| Вопросы учащимся | Примерные ответы |
| 1. По какому признаку мы можем отнести квадратное уравнение к тому или иному виду? | В зависимости от коэффициентов уравнения. |
| 2. Назовите номера полных квадратных уравнений | 1, 3, 4, 6, 9, 10 |
| 3. Назовите номера приведенных квадратных уравнений | 1,3, 7, 10 |
| 4. Назовите номера неполных квадратных уравнений | 2, 5, 7, 8 |
| 5. Запишите квадратное уравнение, у которого свободный член равен 6, первый коэффициент равен 1, а второй, равен –12. Как оно называется? |  -12x+6=0 -12x+6=0
|
| 6. От чего зависит количество корней квадратного уравнения? | От знака дискриминанта. |
3. Математическая разминка (письменно) – 10 мин.
Ребята, 2011 год в Российской Федерации «Годом российской космонавтики», а из какого языка к нам пришло слово «космос»? Для ответа на этот вопрос решите уравнение и по таблице определите: 2 -7x+6=0
-7x+6=0
| Язык | Корни уравнения |
| Английский | -1,5;2 |
| Латинский | 3; 4 |
| Греческий | 1,5; 2 |
| Немецкий | -2; 1,5 |
| Французский | -3; 4 |
Теперь, когда вы узнали, что слово «космос» пришло к нам из греческого языка, давайте, определим, что оно означает в переводе на русский язык.
Для этого решите неполные квадратные уравнения и запишите в таблицу буквы, соответствующие найденным ответам и составьте из них слово, некоторые буквы можно использовать несколько раз, что у вас получилось?
3 +27=0; Н
+27=0; Н
2=7 +2; В
+2; В
4 +х=0; Е
+х=0; Е
9 –4=0; С
–4=0; С
0,5 – 32 =0; А
– 32 =0; А
(х–4)(2х+7)=0 Л
5 –125=0 Я
–125=0 Я
| 0 | +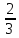 , - , -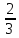 | 0; -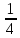 | -3,5; 4 | Нет действительных корней | 8 | ±5 |
| В | С | Е | Л | Н | А | Я |
Итак, «космос» - kosmos – это вселенная.
4. Математический диктант – 5 мин.
Сейчас я диктую вам уравнения, вы пишите решение самостоятельно в тетрадь. Кто не успел, тот ставит прочерк.
1. =13 x=
=13 x=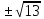
2.  = 49 x=
= 49 x=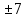
3.  = - 28 решений нет
= - 28 решений нет
4.  = 1 x=1
= 1 x=1
5.5 =20 x=
=20 x=
6.(х–2)(x+3)=0 x= ; х=-3
; х=-3
Взаимопроверка тетрадей. Каждый правильный ответ оценим 1 баллом.
Физкультминутка – 3 мин.
Буквоград – 10 мин.
А сейчас узнаем, какой российский космонавт 50 лет назад полетел в космос. Давайте проанализируем высказывания и определим фамилию космонавта.
Зачеркните в таблице буквы, обозначающие ложные высказывания (номер высказывания совпадает с порядковым номером буквы). Из оставшихся букв получите слово.
1. Уравнение  +9=0 имеет два корня.
+9=0 имеет два корня.
2.В уравнении  -2x+1=0 единственный корень.
-2x+1=0 единственный корень.
3. В уравнении  -5x+3=0 сумма корней равна - 5.
-5x+3=0 сумма корней равна - 5.
4. Уравнение  -8x-3=0 не имеет корней.
-8x-3=0 не имеет корней.
5. Корни уравнения  -4х =0 являются противоположными числами. 6. Корни уравнения
-4х =0 являются противоположными числами. 6. Корни уравнения  – 0,16 = 0 равны 0, 4 .
– 0,16 = 0 равны 0, 4 .
7. Уравнение  -9x+8=0 является неполным.
-9x+8=0 является неполным.
8. Произведение корней уравнения  -11x+9=0 равно - 9.
-11x+9=0 равно - 9.
9. . В уравнении  +8x=0 один из корней – отрицательное число. 10. Уравнение
+8x=0 один из корней – отрицательное число. 10. Уравнение  = – 4 имеет один корень.
= – 4 имеет один корень.
11. Корнями уравнения  -100x+99=0 являются числа 99 и 1.
-100x+99=0 являются числа 99 и 1.
12. В уравнении  =0 дискриминант равен 0.
=0 дискриминант равен 0.
13. Уравнение 3 + 9= 0 не имеет корней.
+ 9= 0 не имеет корней.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| М | Г | А | Т | Л | Г | Д | А | Р | П | И | У | Н |
В результате вычёркивания букв должно получиться: ГАГАРИН
7. Повторение теоремы Виета – 3 мин.
Давайте вспомним как, не производя вычислений, можно ответить на вопрос: «Чему равна сумма и произведение корней квадратного уравнения?» (По теореме Виета).
Устно найдем корни уравнений по теореме Виета:
 5x60
5x60
 9x200 (ответы:3 и 2; 4 и 5; -2 и -1)
9x200 (ответы:3 и 2; 4 и 5; -2 и -1)
 3x20
3x20
8. Самостоятельная работа – 5 мин.
Урок подходит к концу. Сегодня мы повторили все необходимые математические понятия, формулы и способы решения квадратных уравнений. Итогом нашего урока будет небольшая самостоятельная работа. Ребята, выполнившие работу быстро, могут решить дополнительно задание, написанное на доске.
| Вариант 1– А. | Вариант 2 – А. |
| Решите квадратные уравнения: | Решите квадратные уравнения: |
| 3 480 480 5 0 0  6x0 6x0  4x30 4x30
| 9 0 0  14x0 14x0 7 280 280  6x50 6x50
|
| Один из корней квадратного уравнения  xa0 равен 4. Найдите число a. xa0 равен 4. Найдите число a. | Один из корней квадратного уравнения  ax80 равен 4. Найдите число a. ax80 равен 4. Найдите число a. |
Дополнительные задания.
| Вариант 1-Б | Вариант 2-Б |
| Решить квадратные уравнения: 9x3 0 0  2x630 2x630 2 5x20 5x20
 4 4 x120 x120 | Решить квадратные уравнения: 8x2 0 0  18x650 18x650 2 3x20 3x20  2 2 x10 x10 |
| При каких значениях c уравнение  10xc0 не имеет корней. 10xc0 не имеет корней. Приведите пример. | При каких значениях c уравнение  8xc0 имеет два корня. 8xc0 имеет два корня. Приведите пример. |
Тетради с решением учащиеся сдают на проверку.
9. Подведение итогов – 2 мин.
Список литературы:
1. Никольский С. М., Потапов М. К., Решетников Н.Н., Шевкин А. В. Алгебра 8. – М.: Просвещение, 2016.
2. Потапов М. К., Шевкин А.В. Дидактические материалы по алгебре, 8 класс. – М.: Просвещение, 2017.
3. Потапов М. К., Шевкин А. В. Тесты по алгебре: 8 класс: к учебнику Никольский С. М., и др. Алгебра 8. – М.: Просвещение, 2016.







 +9x–12=0;
+9x–12=0; 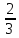 , -
, -