Сафоновский филиал областного государственного бюджетного профессионального образовательного учреждения
«Смоленская академия профессионального образования»
(Сафоновский филиал ОГБПОУ СмолАПО)
Цикловая комиссия общеобразовательных дисциплин
Методические указания по выполнению
внеаудиторных самостоятельных работ
по дисциплине «Математика»
преподавателя Поповой Л.М.
Уважаемые студенты!
Для успешного усвоения материала по дисциплине «Математика» необходимо не только ваше присутствие на учебных занятиях, но и выполнение дополнительных самостоятельных заданий. Для систематизации этой работы вам предлагаются «Методические указания по выполнению внеаудиторных самостоятельных работ по дисциплине «Математика».
В «Методических указаниях» представлен перечень самостоятельных работ, где отражены все разделы дисциплины, указан вид самостоятельной деятельности и примерное количество времени, отводимое на выполнение каждой работы.
В «Приложениях» формулируются конкретные задания по изучаемым раздела курса.
Перед тем как приступить к выполнению практических заданий, повторите материал изученной темы по учебникам и конспектам учебных занятий. Обратите внимание на перечисленные знания и умения, которыми должен овладеть студент после изучения темы.
Выполнение заданий для внеаудиторной самостоятельной работы поможет вам глубже овладеть практическими навыками в решении упражнений по математике.
В конце рекомендаций приведен список литературы, которая поможет не только повторить и закрепить знания, но и осмыслить их по-новому.
Контроль за эффективностью самостоятельных работ осуществляется:
через собеседование на практических занятиях;
через проверку письменных работ;
во время индивидуальных консультаций;
на проверочных работах.
Самостоятельная (внеаудиторная) работа
студентов I курсов по дисциплине «Математика» на I семестр
| № п/п | Раздел (Тема) | Вид работы | Кол-во часов | Приложение |
| Раздел 1. Развитие понятия о числе |
| 1.1. | Действительные числа. | Решение упражнений: «Вычисление значений числовых выражений» Подготовка сообщений на тему: «Непрерывные дроби» |
4 |
Приложение № 1 |
| 1.2. | Приближенные вычисления. | Решение упражнений: «Вычисление значения числового выражения с заданной точностью на инженерном калькуляторе» |
2 |
Приложение № 2 |
| 1.3. | Комплексные числа | Решение упражнений: «Выполнение действий над комплексными числами», «Переход от одной формы записи комплексного числа к другой» |
4 |
Приложение № 3 |
| Раздел 2. Координаты и векторы |
| 2.1.
| Координаты и векторы | Решение упражнений: «Решение практических задач с применением векторов» Выполнение тестовых заданий «Координаты и векторы в пространстве». Подготовка сообщений на тему «Векторное задание прямых и плоскостей в пространстве». |
6 |
Приложение № 4 |
| Раздел 3. Уравнения и неравенства. Системы уравнений |
| 3.1. | Уравнения и неравенства. Системы уравнений | Решение упражнений: «Решение уравнений и неравенств различных видов»; «Решение систем линейных уравнений»; «Решение текстовых задач». Подготовка сообщений « Исследование уравнений и неравенств с параметром»; «Решение неравенств, содержащих переменную под знаком модуля». |
10 |
Приложение № 5 |
| Раздел 4. Функции, их свойства и графики |
| 4.1. | Числовая функция, ее свойства и график | Решение упражнений «Нахождение области определения функций» «Построение графиков функций с помощью простейших преобразований» Составление таблицы «Основные элементарные функции, их свойства и графики»
|
6 |
Приложение № 6 |
| 4.2. | Предел функции | Решение упражнений «Вычисление пределов функций. Раскрытие неопределенностей» Выполнение тестовых заданий «Вычисление пределов функций» |
4 |
Приложение № 7 |
| Раздел 5. Показательная, логарифмическая и степенная функции |
| 5.1. | Корни, степени и логарифмы | Решение упражнений «Выполнение действий над степенными, показательными и логарифмическими выражениями» «Вычисление значений показательных и логарифмических выражений с помощью микрокалькуляторов» Выполнение тестовых заданий «Основные свойства логарифмов» |
6 |
Приложение № 8 |
| 5.2. | Показательная, логарифмическая и степенная функции, их свойства и графики | Решение упражнений «Графический способ решения уравнений» «Исследование показательных, логарифмических функций по их графикам» Выполнение тестовых заданий «Свойства показательной, логарифмической и степенной функций» |
6 |
Приложение № 9 |
| 5.3. | Показательные и логарифмические уравнения и неравенства | Решение упражнений «Решение показательных и логарифмических уравнений и неравенств» Подготовка сообщений «Графическое решение уравнений и неравенств» |
6 |
Приложение № 10 |
| Раздел 6. Основы тригонометрии |
| 6.1. | Тождественные преобразования тригонометрических выражений | Решение упражнений: «Тождественные преобразования тригонометрических выражений» Выполнение тестовых заданий «Формулы тригонометрии» |
4 |
Приложение № 11 |
| 6.2. | Свойства и графики тригонометрических функций | Решение упражнений: «Построение графиков тригонометрических функций с помощью геометрических преобразований» Подготовка сообщений «Сложение гармонических колебаний» |
4 |
Приложение № 12 |
| 6.3. | Тригонометрические уравнения и неравенства | Решение упражнений: «Решение тригонометрических уравнений и неравенств» |
4 |
Приложение № 13 |
Приложение № 1
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Действительные числа»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава1
А.А.Дадаян «Сборник задач по математике», глава 2
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Выполните действия:
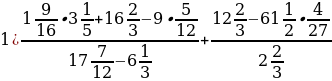
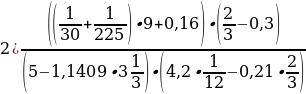
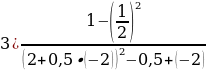
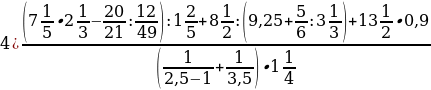
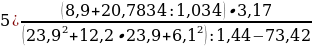
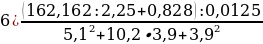
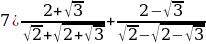
Задание 2. Освободиться от иррациональности в знаменателе:
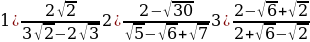
Задание 3. Подготовить сообщение на тему: «Непрерывные дроби»
Приложение № 2
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Приближенные вычисления»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 2
А.А.Дадаян «Сборник задач по математике», §2.7
Н.В. Богомолов «Практические занятия по математике», раздел 1
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Калькулятор студента показывает результат 123,123. Если студент решил, что это число в действительности имеет только три значащие цифры, то нужно оценить, каковы его абсолютная и относительная погрешности.
Задание 2. Решите упражнения:
Найдите периметр треугольника АВС, если АВ=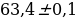 ; ВС=
; ВС=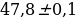 ; СА=
; СА=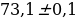 .
.
Найдите площадь прямоугольника ширины 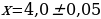 и длины
и длины 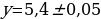 .
.
Найдите значение выражения 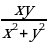 ,если
,если
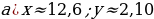
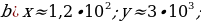
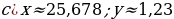
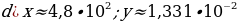
Для вычислений рекомендуется пользоваться инженерным калькулятором.
Задание 3. Используя правила подсчета погрешностей суммы, разности, произведения и частного, вычислите следующие выражения с оценкой погрешности
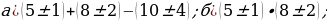
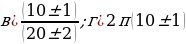
Приложение № 3
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Комплексные числа»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 16
А.А.Дадаян «Сборник задач по математике», глава 16
Н.В. Богомолов «Практические занятия по математике», глава 14
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Закончите определения:
а) Комплексным числом называется…
б) Числа 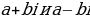 называются…
называются…
в) Два комплексных числа называют равными, если…
г) Модулем комплексного числа называется..
д) Аргументом комплексного числа называется…
е) Тригонометрическая форма комплексного числа-…
ж) Показательная форма комплексного числа-…
Задание 2. Выполните упражнения:
Найдите сумму, разность, произведение и частное следующих чисел:
а) 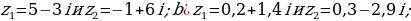
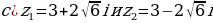
Выполните указанные действия:
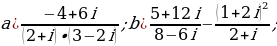
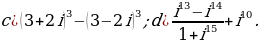
Решите уравнения:
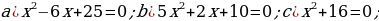
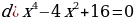 .
.
Представьте комплексные числа в тригонометрической и показательной формах:
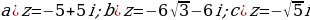
Представьте комплексные числа в алгебраической форме:
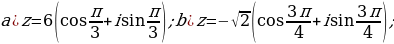
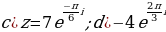
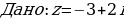 . Найдите
. Найдите 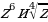 .
.
Приложение № 4
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Координаты и векторы»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 3
А.А.Дадаян «Сборник задач по математике»
Н.В. Богомолов «Практические занятия по математике», главы 17;21;22
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Решите упражнения:
Концы однородного стержня находятся в точках А(2;3) и В(-4;5). Найдите координаты центра тяжести этого стержня.
Найдите величину силы 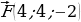 и углы, которые вектор
и углы, которые вектор 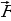 образует с осями координат.
образует с осями координат.
На реактивный самолет в вертикальном направлении действуют сила тяжести 600кН и подъемная сила 650кН, а в горизонтальном направлении- сила тяги 200кН и сила сопротивления воздуха 150кН. Найдите величину и направление равнодействующих сил.
Вычислите скалярное произведение 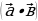 , если
, если 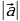 = 8,
= 8, 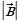 = 5 и
= 5 и 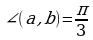 .
.
Найдите координаты вектора 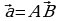 , если точки А и В имеют следующие координаты:
, если точки А и В имеют следующие координаты:
а) А (3; 1), В (5; 0)
б) А (-1; 3), В (-2; 1)
в) А (3; 1), В (-1; -3)
Даны векторы 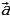 (3; 2;-3) и
(3; 2;-3) и 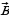 (-2; 6;-1). Найдите векторы:
(-2; 6;-1). Найдите векторы:
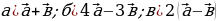
Найдите угол между векторами 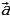 (-1; 2; -2) и
(-1; 2; -2) и 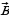 (6; 3; -6).
(6; 3; -6).
Задание 2. Подготовьте сообщение на тему «Векторное задание прямых и плоскостей в пространстве».
Приложение № 5
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Уравнения и неравенства. Системы уравнений»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 3
А.А.Дадаян «Сборник задач по математике»
Н.В. Богомолов «Практические занятия по математике», главы 17;21;22
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Решите уравнения:
3(1 + х) – 4 = 2(1 – 2х); 2) 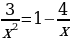 ; 3) 6х2 – х – 1 = 0;
; 3) 6х2 – х – 1 = 0;
4)(2х2 + 3х)2 – 7(2х2 + 3х) + 10 = 0; 5) 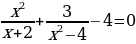 ;
;
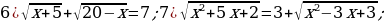
8) 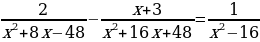
Задание 2. Решите неравенства:
1) 8х – 3(х – 2) 9х – 2; 2) 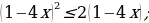 3) – х2 + 8х – 15 0;
3) – х2 + 8х – 15 0;
4) 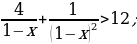 5)
5) 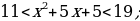 6)
6) 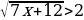 .
.
Задание 3. Решите системы уравнений:
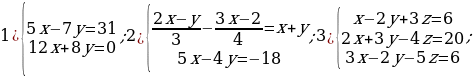
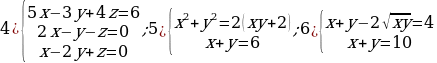
Задание 4. Решите следующие задачи:
Скорый поезд был задержан у семафора на 16 минут и нагнал опоздание на перегоне в 80 километров, идя со скоростью, на 10 км/ч большей, чем полагалось по расписанию. Какова скорость поезда по расписанию?
Моторная лодка спустилась по течению на 28 км и затем вернулась назад. На путь туда и обратно ей потребовалось 7ч. Найдите скорость движения лодки в стоячей воде, если известно, что вода в реке движется со скоростью 3км/ч.
Двое рабочих, работая вместе, выполняют некоторую работу за 8 часов. Первый из них, работая отдельно, может выполнить всю работу на 12 часов скорее, чем второй, если этот последний будет работать отдельно. За сколько часов каждый из них, работая отдельно, может выполнить всю работу?
Один сплав состоит из двух металлов А и В, входящих в отношении 1:2, а другой содержит те же металлы в отношении 2:3. Сколько частей каждого сплава нужно взять, чтобы получить третий сплав, содержащий те же металлы в отношении 17:27?
Из двух жидкостей, удельный вес которых 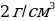 и
и 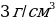 соответственно, составлена смесь. Сколько граммов взято каждой жидкости и каков удельный вес смеси, если 4
соответственно, составлена смесь. Сколько граммов взято каждой жидкости и каков удельный вес смеси, если 4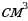 смеси весит в 10 раз меньше, чем вся вторая жидкость, а 50
смеси весит в 10 раз меньше, чем вся вторая жидкость, а 50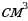 смеси весят столько же, сколько вся вторая жидкость, входящая в т же смесь? Предполагается, что объем смеси равен сумме объемов его составных частей.
смеси весят столько же, сколько вся вторая жидкость, входящая в т же смесь? Предполагается, что объем смеси равен сумме объемов его составных частей.
Задание 5. Подготовьте сообщения на темы:
« Исследование уравнений и неравенств с параметром»;
«Решение неравенств, содержащих переменную под знаком модуля».
Приложение № 6
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Числовая функция, ее свойства и графики»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», §5.1-5.10
А.А.Дадаян «Сборник задач по математике», §5.1-5.3
Н.В. Богомолов «Практические занятия по математике», глава 4,§1.
Рабочая тетрадь по математике (часть1), стр.4-14
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Закончите определения:
Функцией называется…
Переменную х называют … переменной или …, а переменную у- …
Значение у, соответствующее заданному значению х, называют …
Область определения функции- это …
Множество значений функции- …
Графиком функции y=f(x) называется …
Задание 2. Найдите область определения следующих функций:
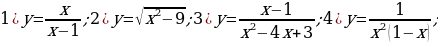
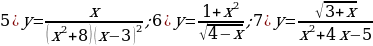
Задание 3. В одной и той же системе координат постройте графики
следующих функций:
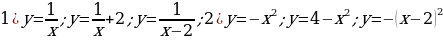
Используя преобразования, постройте графики следующих функций:
1) 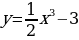 ; 2)
; 2) 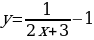 ;
; 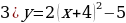
Задание 4. Для систематизации учебного материала по теме «Основные элементарные
функции, их свойства и графики» составьте таблицу:
| Название функции | Формула, задающая функцию | График функции | Основные свойства функции |
|
|
|
|
|
Приложение №7
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Предел функции»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 3
А.А.Дадаян «Сборник задач по математике»
Н.В. Богомолов «Практические занятия по математике», главы 17;21;22
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Закончите определения:
а) Число А называют пределом числовой последовательности 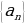 , если …
, если …
Записывают …
б) Пусть дана функция 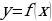 . Если аргумент х, изменяясь, стремится к некоторому числу а и при этом значение функции неограниченно приближается к числу А, тогда говорят, что…
. Если аргумент х, изменяясь, стремится к некоторому числу а и при этом значение функции неограниченно приближается к числу А, тогда говорят, что…
Записывают…
в) Величина, предел которой равен нулю, называется…
г) Величина, предел которой равен бесконечности, называется…
Задание 2. Сформулируйте теоремы о пределах.
Задание 3. Запишите формулы замечательных пределов.
Задание 4. Вычислите пределы функций:
Приложение № 8
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Корни, степени и логарифмы»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 6 §1; 4-5
А.А.Дадаян «Сборник задач по математике» глава 6 §1
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Закончите формулы:
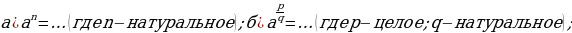

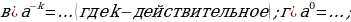

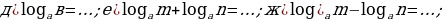
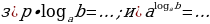
Задание 2. Вычислите:
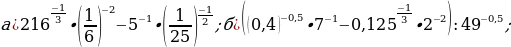
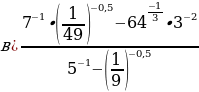
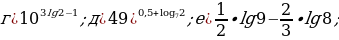
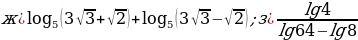
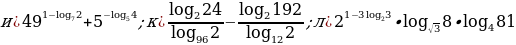
Задание 3. Вычислите значения х
1) 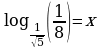 2)
2) 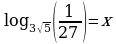 3)
3) 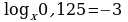 4)
4) 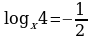
5) 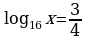 6)
6) 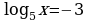 7)
7) 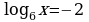 8)
8) 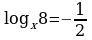
Приложение № 9
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Показательная, логарифмическая и степенная функции, их свойства и графики»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 6 §2-4
А.А.Дадаян «Сборник задач по математике» глава 6 §3
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Заполните таблицу:
| Название функции | Формула, задающая функцию | График функции | Основные свойства функции |
| 1. показательная |
|
|
|
| 2. логарифмическая |
|
|
|
| 3. степенная |
|
|
|
Задание 2. Решите уравнения графически:
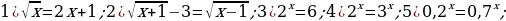
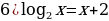
Задание 3.Постройте графики следующих функций и перечислите их основные свойства:
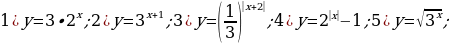
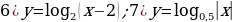
Приложение № 10
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Показательные и логарифмические уравнения и неравенства»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 6 §7
А.А.Дадаян «Сборник задач по математике» глава 6 §4-7
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Решите уравнения:
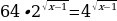
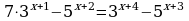
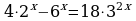
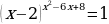
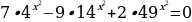
6) 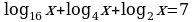
7) 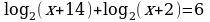
8) 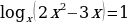
9) 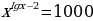
10) 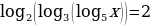
Задание 2. Решите неравенства:
1) 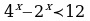 3)
3) 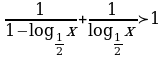
2) 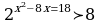 4)
4) 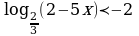
Задание 3. Решите системы:
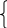
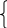 1)
1) 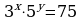 2)
2) 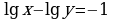
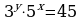
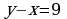
Задание 4. Подготовить сообщение на тему «Графическое решение уравнений и неравенств»
Приложение № 11
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Тождественные преобразования тригонометрических выражений»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 7 §1-12
А.А.Дадаян «Сборник задач по математике» глава 7 §1-3
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Закончите формулы:
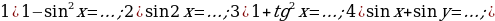
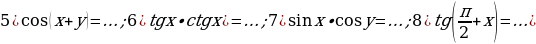
Задание 2. Вычислите:
1) sinα, tgα, ctgα, если 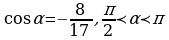
2) sin2α, cos2α, tg2α, если 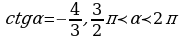
3) 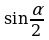 ,
, 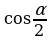 ,
, 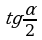 , если
, если 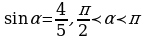
Задание 3. Упростите выражение:
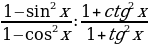
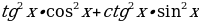
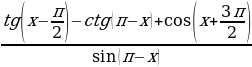
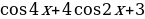
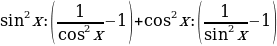
Задание 4. Определите знак выражения:
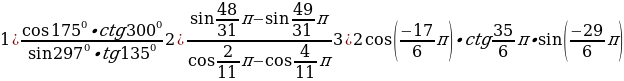
Задание 5. Докажите тождество:
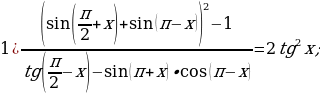
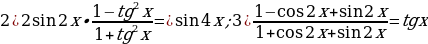
Приложение № 12
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Свойства и графики тригонометрических функций»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 7 §14
А.А.Дадаян «Сборник задач по математике» глава 7
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Заполните таблицу:
| Функция | График функции | Основные свойства функции |
| 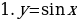
|
|
|
| 2.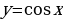 |
|
|
| 3. 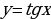 |
|
|
Задание 2. Постройте в одной системе координат графики функций:
y = sin x; y=3sinx; y= sin(x-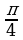 ); y = 3sin(x-
); y = 3sin(x-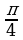 ); y=3 sin(2x-
); y=3 sin(2x-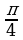 )
)
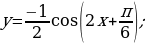
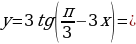
Задание 3. Подготовить сообщение на тему «Сложение гармонических колебаний»
Приложение № 13
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Тригонометрические уравнения и неравенства»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 7 §16-17
А.А.Дадаян «Сборник задач по математике» глава 7 §4-5
конспекты учебных занятий
и выполните следующие задания:
Задание 1. Заполните таблицу:
| Простейшие тригонометрические уравнения | решение |
| sin x=b |
|
| cos x=b
|
|
| tg x=b |
|
Задание 2. Решите уравнения
1) 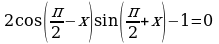
2) 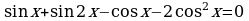
3) 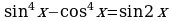
4) 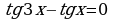
5) 
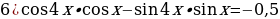
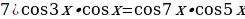
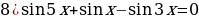
Задание 3. Решите неравенства
1) 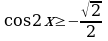
2) 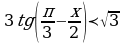
3) 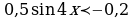
Самостоятельная (внеаудиторная) работа
студентов I курсов по дисциплине «Математика» I I семестр
| № п/п | Раздел (Тема) | Вид работы | Кол-во часов | Приложение |
|
Раздел 7.Прямые и плоскости в пространстве
|
|
7.1. |
Прямые и плоскости в пространстве
| Решение задач по темам: «Параллельность в пространстве» «Перпендикулярность в пространстве» «Изображение пространственных фигур на плоскости» Выполнение тестовых заданий «Взаимное расположение прямых и плоскостей в пространстве» Учебно-исследовательская работа «Параллельное проектирование» |
10 |
Приложение № 14 |
|
Раздел 8. Начала математического анализа
|
|
8.1. |
Производная функции
| Решение упражнений по темам: «Техника дифференцирования» «Нахождение скорости для процесса, заданного формулой и графиком» «Вычисление приближенных значений величин с помощью производной» Выполнение тестовых заданий «Нахождение производных функций» |
8 |
Приложение № 15 |
|
8.2. |
Исследование функций с помощью производной | Решение упражнений по темам: «Построение графиков функций с помощью производных» «Использование производной для нахождения наилучшего решения в прикладных задачах» Выполнение тестовых заданий «Приложение производной к исследованию свойств функции» Учебно-исследовательская работа «Применение производной к решению прикладных задач» |
10 |
Приложение № 16 |
|
8.3 |
Неопределенный интеграл | Решение упражнений по теме: «Вычисление неопределенных интегралов» Выполнение тестовых заданий «Неопределенный интеграл и его свойства» |
6 |
Приложение № 17 |
|
8.4. |
Определенный интеграл | Решение упражнений по темам: «Методы вычисления определенного интеграла»; «Приложения определенного интеграла». Составление таблицы для систематизации учебного материала «Вычисление площадей плоских фигур» Учебно-исследовательская работа «Применение определенного интеграла к решению физических и технических задач» |
10 |
Приложение № 18 |
|
Раздел 9.Геометрические тела и поверхности
|
|
9.1. |
Многогранники | Решение упражнений по теме: «Нахождение основных элементов призм и пирамид» «Построение сечений многогранников. Площади сечений» Учебно-исследовательская работа «Применение золотого сечения» |
6 | Приложение № 19 |
|
9.2. |
Тела вращения | Решение упражнений по теме: «Нахождение основных элементов цилиндра, конуса и шара» Учебно-исследовательская работа. «Построение сечений тел вращения» |
4 | Приложение № 20 |
|
Раздел 10. Измерения в геометрии
|
|
10.1. |
Измерения в геометрии | Решение упражнений по темам: «Вычисление площадей поверхностей и объемов геометрических тел» «Вычисление площадей поверхностей и объемов комбинированных тел» |
6 |
Приложение № 21 |
|
Раздел 11. Комбинаторика, статистика и теория вероятностей
|
|
11.1. |
Элементы комбинаторики | Решение упражнений по темам: «Доказательство утверждений с помощью метода математической индукции» «Элементы комбинаторики» Выполнение тестовых заданий «Размещения, перестановки, сочетания» |
6 |
Приложение № 22 |
|
11.2. |
Элементы теории вероятностей | Решение упражнений по теме: «Вычисление вероятностей событий». Выполнение тестовых заданий «Теория вероятностей» |
6 |
Приложение № 23 |
|
11.3. |
Элементы математической статистики
| Решение упражнений по теме: «Построение таблиц, диаграмм, графиков, представляющих статистические данные» Учебно-исследовательская работа. «Средние значения и их применение в статистике» |
7 |
Приложение № 24 |
Приложение 14.
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Прямые и плоскости в пространстве»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 8;
А.А.Дадаян «Сборник задач по математике», глава 8;
конспекты учебных занятий и выполните следующие задания:
Задание 1. Закончите определения:
Две прямые в пространстве называются параллельными, если…
Скрещивающиеся прямые- это…
Прямая и плоскость называются параллельными, если…
Две плоскости называются параллельными, если…
Две прямые в пространстве называются перпендикулярными, если…
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если…
Две пересекающиеся плоскости называются перпендикулярными, если…
Задание 2. Составьте схемы:
а) взаимного расположения двух прямых в пространстве
б) взаимного расположения прямой и плоскости
| Прямая а и плоскость  |
в) взаимного расположения двух плоскостей в пространстве
| Две плоскости 
|
Задание 3. Сформулируйте следующие теоремы:
а) признак параллельности прямой и плоскости в пространстве;
б) признак параллельности двух плоскостей в пространстве;
в) теорему о трех перпендикулярах;
г) свойства параллельных плоскостей.
Задания для самостоятельного решения:
«Параллельность в пространстве»
№1. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и если АА1=5см, ВВ1=7см.
№2. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найдите длину отрезка ВВ1, если АВ=6см; АС:СС1=2:5.
№3. Дана трапеция АВСД, основания- АД и ВС. Точка Р не принадлежит плоскости трапеции. Докажите, что прямая, проходящая через середины отрезков РВ и РС, параллельна средней линии трапеции.
№4. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС- в точке В1. Найдите длину отрезка А1В1, если а) АВ=15см, АА1:АС=2:3; б) В1С=10см, АВ:АС=4:5.
№5.через вершины параллелограмма АВСД, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие другую плоскость в точках А1, В1, С1 и Д1. Докажите , что четырехугольник А1В1С1Д1 тоже параллелограмм.
№6. Через вершины треугольника АВС, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие другую плоскость в точках А1, В1, С1. Докажите равенство треугольников АВС и А1 В1 С1.
№7. Три прямые, проходящие через одну точку, пересекают данную плоскость в точках А, В и С, а параллельную ей плоскость в точках А1, В1 и С1. Докажите подобие треугольников АВС и А1 В1 С1.
«Перпендикулярность в пространстве»
№1. Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от вершин треугольника.
№2. Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от сторон треугольника.
№3. Из точки к плоскости проведены две наклонные, равные 10см и 17см. разность проекций этих наклонных равна 9см. найдите проекции наклонных.
№4. Из точки к плоскости проведены две наклонные, равные 23см и 33см. найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
№5. Телефонная проволока длиной 15м протянута от телефонного столба, где она прикреплена на высоте 8м от поверхности земли, к дому, где ее прикрепили на высоте 20м. найдите расстояние между домом и столбом, предполагая, что проволока не провисает.
№6. Из вершины равностороннего треугольника АВС восставлен перпендикуляр АД к плоскости треугольника. Найдите расстояние от точки Д до стороны ВС, если АД=13см, ВС=6см.
№7. Из данной точки к плоскости проведены две равные наклонные длиной 2м. найдите расстояние от точки до плоскости, если наклонные образуют угол 600, а их проекции перпендикулярны.
№8. Два равнобедренных треугольника имеют общее основание, а их плоскости образуют угол 600. Общее основание равно 16м, боковая сторона одного треугольника 17м, а боковые стороны другого перпендикулярны. Найдите расстояние между вершинами треугольников.
№9. Равнобедренные треугольники АВС и АВД с общим основанием АВ лежат в разных плоскостях, угол между которыми равен 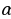 . Найдите
. Найдите 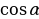 , если АВ=24м, АС=13м, АД=37м, СД=35м.
, если АВ=24м, АС=13м, АД=37м, СД=35м.
№10. Катеты прямоугольного треугольника равны 7м и 24м. найдите расстояние от вершины прямого угла до плоскости, которая проходит через гипотенузу и составляет угол 300 с плоскостью треугольника.
«Изображение пространственных фигур на плоскости»
№1. Постройте изображение произвольного треугольника, полученного путем параллельного проектирования, и изображение его биссектрис и высот.
№2. Постройте изображение окружности, описанной около правильного треугольника; равнобедренного треугольника; прямоугольника; правильного шестиугольника при параллельном проектировании.
№3. Постройте изображение окружности, вписанной в правильный треугольник; равнобедренный треугольник; квадрат; ромб; правильный шестиугольник.
Учебно-исследовательская работа: тема «Параллельное проектирование».
Приложение 15.
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Производная функции»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 9;
А.А.Дадаян «Сборник задач по математике», глава 9;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. а) Закончите определение
Производной функции 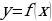 в точке
в точке 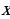 называется …
называется …
б)Сформулируйте основные правила дифференцирования:
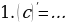
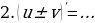
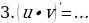
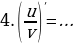
в)Закончите формулировку правила:
Производная сложной функции f(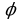 (x)) равна произведению …:
(x)) равна произведению …:
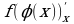 … .
… .
Производной n-ого порядка от функции 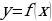 называется…
называется…
т.е. 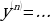
г) Раскройте геометрический смысл производной:
Производная функции 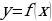 при заданном значении аргумента
при заданном значении аргумента 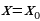 равна …
равна …
Уравнение касательной к графику функции 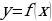 в точке
в точке 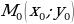 имеет вид…
имеет вид…
Уравнение нормали, т.е. прямой, проходящей через точку касания 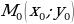 перпендикулярно касательной, записывается в виде…
перпендикулярно касательной, записывается в виде…
д) Раскройте механический смысл производной:
Производная от функции 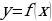 , вычисленная при значении аргумента
, вычисленная при значении аргумента 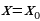 , представляет собой скорость изменения этой функции относительно независимой переменной
, представляет собой скорость изменения этой функции относительно независимой переменной 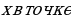
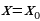 .
.
В частности, если зависимость между пройденным путем S и временем t при прямолинейном движении выражается формулой S=S(t), то 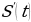 есть… ,а
есть… ,а 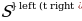 - …
- …
е)Закончите формулы:
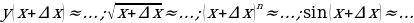
Задания для самостоятельного решения:
«Техника дифференцирования»
№1-№4. Найдите производные функций.
№1. 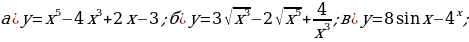
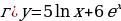 .
.
№2. 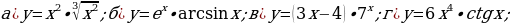
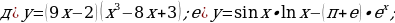
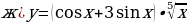 .
.
№3. 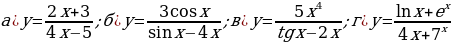 .
.
№4. 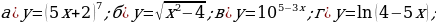
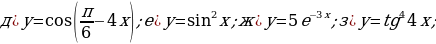
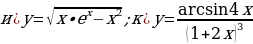 .
.
№5. Найдите производную функции в точке 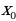 :
:
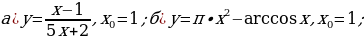
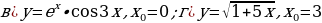 .
.
№6. Найдите производные второго и третьего порядков от следующих функций:
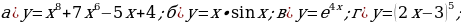
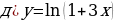 .
.
«Нахождение скорости для процесса, заданного формулой и графиком»
№1. 1) Уравнение движения точки по оси Ox есть 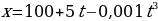 . Найдите
. Найдите
скорость и ускорение точки для моментов времени 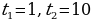 .
.
2) По оси Ох движутся две точки, имеющие законы движения
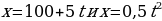 .
.
С какой скоростью будут двигаться эти точки в момент встречи?
3) С крыши дома высотой 20 м брошен вверх металлический шарик с начальной
скоростью 39,2 м/с. Определите: а) скорость шарика в конце 2-ой секунды;
б) наибольшую высоту подъема.
4) Докажите, что если тело движется прямолинейно по закону 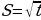 , то его
, то его
ускорение пропорционально кубу скорости.
«Вычисление приближенных значений величин с помощью производной»
№1. На сколько (приблизительно) увеличилось ребро куба, если его объем изменился
с 27 куб.м до 27,2 куб.м?
№2. На сколько приблизительно изменится сторона квадрата, если его площадь
уменьшить с 16 кв.м до 15,82 кв.м?
№3. В результате измерения радиуса круга допущена ошибка в 1%. По найденному
приближенному значению вычислена площадь круга. Какая при этом допущена
погрешность?
№4. Найдите приближенные значения заданных выражений:
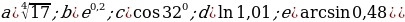
Приложение 16.
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Исследование функций с помощью производной»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 9;
А.А.Дадаян «Сборник задач по математике», глава 9;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. Закончите определения:
1) Функция называется возрастающей в некотором промежутке, если…
2) Функция называется убывающей в некотором промежутке, если…
3) Точка х=х0 называется точкой максимума функции f(x), если…
4) Точка х=х0 называется точкой минимума функции f(x), если…
5) Точками экстремума функции называются точки…
6) Экстремумом функции называется…
7) Функция y=f(x) называется выпуклой вверх на промежутке Х, если…
8) Функция y=f(x) называется выпуклой вниз на промежутке Х, если…
9) Точкой перегиба графика функции называется точка…
Задание 2. Закончите формулировки утверждений:
Для того чтобы функция 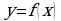 , имеющая на некотором промежутке
, имеющая на некотором промежутке 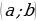 производную
производную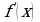 , возрастала на этом промежутке, необходимо и достаточно, чтобы для всех
, возрастала на этом промежутке, необходимо и достаточно, чтобы для всех 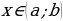 выполнялось неравенство
выполнялось неравенство 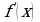 …0
…0
Для того чтобы функция 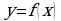 , имеющая на некотором промежутке
, имеющая на некотором промежутке 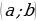 производную
производную 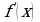 , убывала на этом промежутке, необходимо и достаточно, чтобы …
, убывала на этом промежутке, необходимо и достаточно, чтобы …
Пусть функция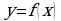 непрерывна в точке
непрерывна в точке 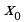 . Если
. Если 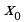 - точка экстремума функции
- точка экстремума функции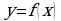 , то в этой точке необходимо одно из следующих условий:
, то в этой точке необходимо одно из следующих условий:
а) либо 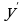 …; б) либо
…; б) либо 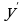 … .
… .
Точки 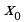 , в которых либо
, в которых либо 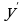 …, либо
…, либо 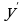 …, называются … точками.
…, называются … точками.
Пусть функция 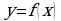 непрерывна на некотором промежуткe
непрерывна на некотором промежуткe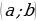 , содержащем критическую точку
, содержащем критическую точку 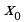 , и дифференцируема на
, и дифференцируема на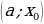 ,
, 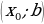 , тогда:
, тогда:
Достаточное условие экстремума по второй производной:
Пусть в точке х0 производная первого порядка равна … и существует производная второго порядка, тогда если 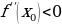 , то х0- точка … функции y=f(x), если
, то х0- точка … функции y=f(x), если 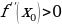 , то х0- точка … функции.
, то х0- точка … функции.
Задание 3. Сформулируйте:
Правило нахождения промежутков монотонности функции
Правило отыскания экстремумов функции с помощью первой производной
Правило нахождения наибольшего и наименьшего значения функции
Правило исследования функции на выпуклость и точки перегиба
Задания для самостоятельного решения:
«Построение графиков функций с помощью производных»
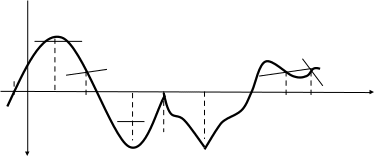
№1. На рисунке дан график функции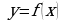 .
.
y
x
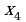
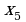
 0
0 
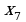
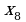
Заполните таблицу, указав знаки 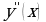 и
и 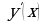 в отмеченных точках:
в отмеченных точках:
№2. Для нижеприведенных функций
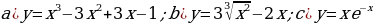
найдите точки экстремума и интервалы монотонности. Заполните таблицы и сделайте схематические чертежи, следуя указанной схеме:
Найдите 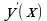 .
.
Определите критические (стационарные) точки.
Определите знаки 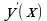 в достаточно малых окрестностях найденных критических точек и точек разрыва функции
в достаточно малых окрестностях найденных критических точек и точек разрыва функции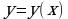 .
.
Заполните таблицу:
| x |
|
|
|
| 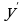
|
|
|
|
| y |
|
|
|
Сделайте чертеж
№3. Исследуйте нижеприведенные функции, а затем постройте их графики:
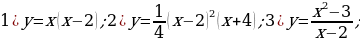
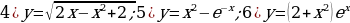
«Использование производной для нахождения наилучшего решения в прикладных задачах»
№1. (задача Дидоны) из имеющихся досок можно сделать забор длиной 1м. Как этим забором огородить прямоугольный двор наибольшей площади, используя в качестве одной стороны стену прилегающего здания?
№2. Из куска проволоки длиной 30см требуется согнуть прямоугольник наибольшей площади. Каковы размеры этого прямоугольника?
№3. Определите размеры открытого бассейна с квадратным дном объемом 100 куб.м, при котором на облицовку его дна и стен пойдет наименьшее количество материала.
№4. Окно имеет форму прямоугольника с полукругом сверху. Периметр окна равен 28м. Каковы должны быть его размеры (ширина и высота), чтобы окно пропускало наибольшее количество света?
№5. Требуется обтесать бревно с круглым сечением диаметром 40см, чтобы получилась балка с прямоугольным сечением наибольшей прочности. (В сопротивлении материалов установлено, что прочность прямоугольной балки пропорциональна 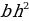 , где -основание прямоугольника в сечении балки,
, где -основание прямоугольника в сечении балки, 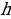 - его высота)
- его высота)
№6. Два тела движутся с постоянными скоростями V1(км/ч) и V2(км/ч) по двум прямым, образующим угол 900 в направлении к вершине этого угла. В начале движения первое тело находилось от вершины на расстоянии 5км, а второе- на расстоянии 8км. Через сколько минут после начала движения расстояние между телами будет наименьшим?
№7. Лодка находится на расстоянии а(км) от ближайшей точки А берега. Пассажир лодки должен попасть в точку В на берегу, находящуюся на расстоянии в(км) от точки А. известны скорость лодки V1(км/ч) и скорость пассажира V2(км/ч). К какому пункту на берегу должна прибыть лодка, чтобы пассажир добрался до точки В за кратчайшее время?
№8. На какой высоте нужно повесить фонарь над центром круглой площадки радиуса а, чтобы площадка была максимально освещена у ее границы?
Учебно-исследовательская работа: тема «Применение производной к решению прикладных задач»
Приложение 17
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Неопределенный интеграл»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 10 §1-5;
А.А.Дадаян «Сборник задач по математике», глава 10 §1-2;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. Закончите определения:
1) Функция F (x) называется первообразной функции f (x) на отрезке [a; b], если 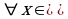 [a; b] справедливо равенство ... .
[a; b] справедливо равенство ... .
2) Если F (x) – первообразная f (x), то …, причём: а) выражение F (x) + C называется … функции … и б) обозначается символом … .
Задание 2. Заполните таблицу:
| Правила интегрирования | Простейшие интегралы |
| 1. 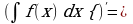 … . … . 2. 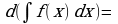 … . … . 3. 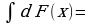 … . … . 4. 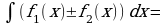 … . … . 5.  … . … . 6. 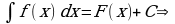 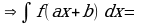 … . … .
| 1. 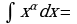 … …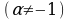 2. 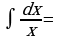 … . … . 3. 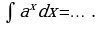 4. 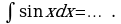
5. 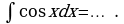 6. 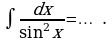 | 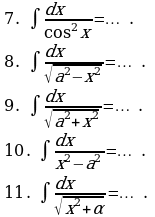
|
Задание 3. а) Закончите формулировку одного из важнейших правил интегрирования:
Пусть известно, что 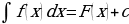 , тогда
, тогда 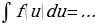 , где u(x) – произвольная дифференцируемая функция от х.
, где u(x) – произвольная дифференцируемая функция от х.
Например: 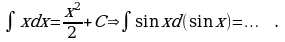
б)Закончите запись формулы интегрирования по частям:
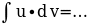
Упражнения для самостоятельного решения
«Нахождение неопределенных интегралов»
№1-№3 Найдите интегралы:
№1. 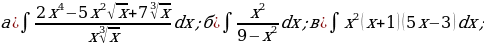
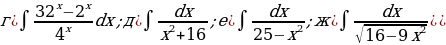
№2. 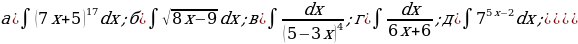
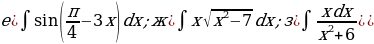
№3. 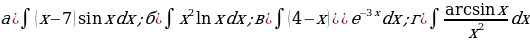
Приложение 18
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Определенный интеграл»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 10 §6-15;
А.А.Дадаян «Сборник задач по математике», глава 10 §3-4;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. Закончите определения:
1). Пусть функция f (x) непрерывна отрезке [a; b], который разбит произвольным образом на n элементарных непересекающихся отрезков 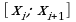 , таких, что
, таких, что 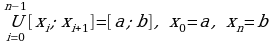 .
.
Пусть на каждом отрезке 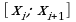 произвольным образом выбрана точка
произвольным образом выбрана точка 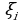 и для каждого значения i вычислено
и для каждого значения i вычислено 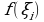 .
.

0 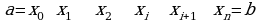 x
x
Тогда интегральной суммой для функции f(x) на отрезке [a, b] называется … .
Замечание. На рисунке рассмотрен случай 0a. Из определения следует, что знаки чисел a и b могут быть … .
2) Если при любых разбиениях отрезка [a, b], таких что 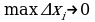 и при любом выборе точки
и при любом выборе точки 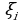 из отрезка
из отрезка 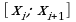 … к одному и тому же пределу, то этот предел называют определенным интегралом от функции f(x) на отрезке [a, b] и обозначают …, причем:
… к одному и тому же пределу, то этот предел называют определенным интегралом от функции f(x) на отрезке [a, b] и обозначают …, причем:
число a называют …;
число b - ….;
функцию f(x) -…;
отрезок [a, b] - ….;
х – … .
Задание 2. Закончите формулировку теоремы существования определенного интеграла:
Если функция f(x) … на отрезке [a, b], то она интегрируется на этом отрезке, т. е. … существует.
Задание 3. Перечислите основные свойства определенного интеграла:
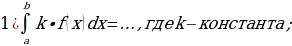
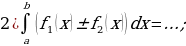
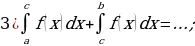
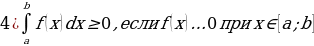
Задание 4. а)Закончите формулировку теоремы Ньютона – Лейбница:
Если F(x) есть какая-либо первообразная функции f(x), то справедлива формула 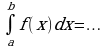
б)Сформулируйте геометрический смысл определенного интеграла.
в). Сформулируйте механический смысл определенного интеграла.
г). Запишите формулу замены переменной при вычислении определенного интеграла.
Упражнения для самостоятельного решения:
«Методы вычисления определенного интеграла»
№1-№3 Вычислите определенные интегралы:
№1.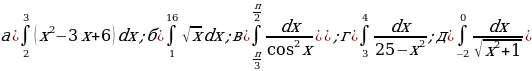
№2. 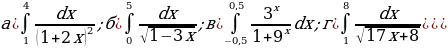
№3. 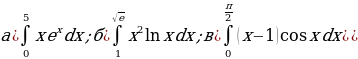
«Приложения определенного интеграла»
№1. Скорость движения задаётся формулой 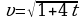 м/с. Найдите путь, пройденный точкой за первые 10 с от начала движения.
м/с. Найдите путь, пройденный точкой за первые 10 с от начала движения.
№2. Какую работу надо затратить, чтобы растянуть пружину на 6 см, если сила в 1 Н растягивает её на 1 см?
№3. Сила тока I в проводнике меняется во времени по закону 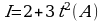 . Найти количество электричества, протекшее через поперечное сечение проводника за время от
. Найти количество электричества, протекшее через поперечное сечение проводника за время от 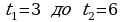 с.
с.
№4. Сила тока (городского), имеющего 50 колебаний в минуту, изменяется по закону 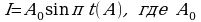 - его амплитуда. Найдите количество электричества, протекшего через поперечное сечение проводника за время от
- его амплитуда. Найдите количество электричества, протекшего через поперечное сечение проводника за время от 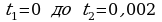 с.
с.
№5. Вычислите площадь:
а) фигуры, ограниченной кривой y = ln x, осью Ox и прямой x = e;
б) фигуры, ограниченной параболой 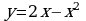 и прямой y = - x;
и прямой y = - x;
в) фигуры, ограниченной параболой 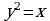 , гиперболой xy = 8 и отрезком прямой, соединяющим точку (8; 1) гиперболы с точкой
, гиперболой xy = 8 и отрезком прямой, соединяющим точку (8; 1) гиперболы с точкой 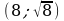 параболы;
параболы;
г) фигуры, ограниченной параболой 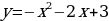 , осями координат и прямой х=2;
, осями координат и прямой х=2;
д) фигуры, ограниченной ветвью гиперболы 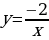 и прямыми х=1 и х=5.
и прямыми х=1 и х=5.
Учебно-исследовательская работа: тема «Применение определенного интеграла к решению физических и технических задач»
Приложение 19
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме «Многогранники»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 12;
А.А.Дадаян «Сборник задач по математике», глава12;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. Дайте определения:
а) многогранника;
б) многогранной поверхности;
в) призмы;
г) параллелепипеда;
д) пирамиды;
е) усеченной пирамиды.
Задание 2. Закончите определения:
Призма называется прямой, если…
Призма называется правильной, если…
Прямоугольным параллелепипедом называется…
Пирамида называется правильной, если…
Правильным называется многогранник, если…
Задание 3. Постройте изображения:
призмы(прямой, наклонной, правильной); пирамиды(обычной, правильной); параллелепипеда(прямого, наклонного, прямоугольного); куба; усеченной пирамиды.
На построенных изображениях укажите основные элементы этих многогранников.
Упражнения для самостоятельного решения:
№1. Боковое ребро прямоугольного параллелепипеда равно 10 см, стороны основания равны
12 см и 16 см, а одна из диагоналей основания равна 24 см. найдите диагонали параллелепипеда.
№2. Основанием прямой треугольной призмы служит прямоугольный треугольник с гипотенузой, равной 3 м, и острым углом 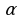 . Через гипотенузу проведена плоскость под углом
. Через гипотенузу проведена плоскость под углом 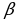 к плоскости основания. Эта плоскость пересекает боковое ребро призмы, выходящее из вершины прямого угла основания. Найдите площадь сечения.
к плоскости основания. Эта плоскость пересекает боковое ребро призмы, выходящее из вершины прямого угла основания. Найдите площадь сечения.
№3.В треугольной пирамиде стороны основания равны 13 см, 14 см, 15 см, все боковые ребра составляют с основанием углы, равные 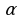 . Найдите высоту пирамиды.
. Найдите высоту пирамиды.
№4. Диагонали трех граней прямоугольного параллелепипеда, сходящиеся в одной вершине, равны 8 м, 10 ми 12 м. Найдите линейные размеры этого параллелепипеда.
№5. В правильной четырехугольной усеченной пирамиде сторона большего основания а, сторона меньшего b. Боковое ребро образует с большим основанием угол 600. Найдите длину бокового ребра.
№6. Построить сечения треугольной призмы АВСА1В1С1 плоскостями, проходящими через точки М, Р и К, лежащими соответственно:
а) на ребрах АА1; ВВ1 и стороне основания АС;
б) на ребрах АА1; ВВ1 и СС1;
в) на сторонах основания АВ; ВС и В1С1.
№7. Постройте сечение пирамиды SABC плоскостью, проходящей через точки M,N и P, лежащие соответственно на ребре AS и гранях ABS и BCS.
Учебно-исследовательская работа: тема «Применение золотого сечения».
Приложение № 20
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Тела вращения»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 13;
А.А.Дадаян «Сборник задач по математике», глава13;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. Дайте определения:
а) тела вращения;
б) цилиндра;
в) конуса;
г) усеченного конуса;
д) шара;
е) сферы.
Задание 2. Постройте изображения:
цилиндра; конуса; усеченного конуса; шара
На построенных изображениях укажите основные элементы этих тел вращения.
Упражнения для самостоятельного решения:
№1. В цилиндр вписана прямая призма, в основании которой – треугольник со сторонами 6 дм и 6 дм и углом 120° между ними. В осевом сечении цилиндра – квадрат. Найти площадь осевого сечения.
№2. Высота прямого кругового конуса равна радиусу основания R. Через вершину проведена плоскость сечения, отсекающая дугу 60°. Найти площадь сечения.
№3. Радиус сферы равен 2,6 дм. Найдите длину линии пересечения сферы плоскостью, находящейся на расстоянии 2,4 дм от ее центра.
№4. Найдите радиус шара, вписанного в правильную n-угольную пирамиду, по длине стороны основания а и плоскому углу 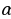 при вершине.
при вершине.
№5. В шар радиуса R вписана правильная четырехугольная пирамида, у которой двугранный угол при боковом ребре равен 2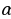 . Найдите длину стороны основания пирамиды.
. Найдите длину стороны основания пирамиды.
Учебно-исследовательская работа: тема «Построение сечений тел вращения»
Приложение № 21
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Измерения в геометрии»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 14;
А.А.Дадаян «Сборник задач по математике», глава14;
и конспекты учебных занятий и выполните следующие задания:
Задание 1. Заполните таблицу:
| Название геометрического тела | Изображение | Основные элементы геометрического тела | Формула для вычисления объема тела | Формула для вычисления площади поверхности |
|
|
|
|
|
|
Задание 2. Решите задачи:
Площади двух граней прямоугольного параллелепипеда равны 20 см2 и 45 см2, длина их общего ребра равна 5 см. Найдите объем параллелепипеда.
Боковое ребро правильной треугольной пирамиды равно 6 см, а плоский угол при вершине равен 60°. Найдите объем пирамиды.
Образующая усеченного конуса равна 15см, боковая поверхность его равна 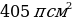 . Высота усеченного конуса в два раза меньше высоты соответствующего полного конуса. Вычислить объем усеченного конуса.
. Высота усеченного конуса в два раза меньше высоты соответствующего полного конуса. Вычислить объем усеченного конуса.
Основанием пирамиды служит равнобедренный треугольник, у которого равные стороны равны 39см, а третья сторона 30см. двугранные углы при основании равны между собой и составляют угол 450. Определить объем этой пирамиды.
В правильной усеченной 4-угольной пирамиде апофема равна 17см. Площадь верхнего основания в 4 раза меньше площади нижнего основания, а площадь боковой поверхности равна 1632см2. Вычислить объем этой усеченной пирамиды.
В полушар радиуса R вписан цилиндр, высота которого равна 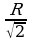 . Найдите объем этого цилиндра.
. Найдите объем этого цилиндра.
Пирамида, основание которой – прямоугольник со сторонами 6 дм и 7 дм, вписана в сферу. Высота пирамиды проходит через вершину основания и равна 6 дм. Найдите площадь сферы.
В цилиндр вписана правильная треугольная призма, сторона основания которого равна а, а боковое ребро – b. Найдите площадь боковой поверхности цилиндра.
Вокруг сферы радиуса 6 см описан усеченный конус, радиусы оснований которого относятся как 4:9. Найдите площадь боковой поверхности усеченного конуса.
Вычислить объем тела, образованного вращением вокруг оси Ох площади, ограниченной линиями: y2=x3; y=2x
Приложение № 22
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Элементы комбинаторики»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 15 §1-4;
А.А.Дадаян «Сборник задач по математике», глава15 §1;
и конспекты учебных занятий и выполните следующие задания:
Задание1. Ответьте на вопросы:
1) Что такое неполная математическая индукция? Приведите примеры.
2) Что такое полная математическая индукция? Приведите примеры.
3) Что называется обобщенным принципом математической индукции? Приведите примеры.
4) Какие множества называются упорядоченными?
5) Что называется перестановкой элементов множества? По какой формуле вычисляется число перестановок?
6) Что называется размещением? По какой формуле вычисляется число размещений?
7) Что называется сочетанием? По какой формуле вычисляется число сочетаний?
8) Перечислите свойства сочетаний.
9) Что такое треугольник Паскаля? Составьте строку треугольника Паскаля для n=6.
10) Напишите формулу бинома Ньютона.
Упражнения для самостоятельного решения:
№1. Методом математической индукции докажите следующие утверждения:
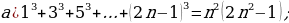
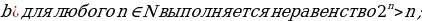
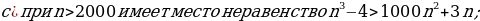
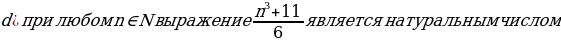 .
.
№2. Сколько существует трехзначных чисел, в записи которых используются лишь цифры 7, 2 и 1?
№3. Сколько существует четных четырехзначных чисел, в записи которых цифры 3, 4, 5 и 6 используются по одному разу?
№4. В автомашине 6 мест. Сколькими способами шесть человек могут сесть в эту машину, если место водителя могут занять только двое из них?
№5. На детской карусели есть 10 одинаковых посадочных мест, расположенных по кругу. Покататься на карусели пришли 9 детей. Сколькими способами их можно рассадить?
№6. Для участия в фотовыставке было отобрано 32 фотографии. На стендах можно разместить только 30 фотографий. Сколько существует различных вариантов размещения 30 фотографий на стендах?
№7. На замке с кодом 10 кнопок с цифрами от 0 до 9. Сколькими способами можно составить шифр из трех цифр, если все они различны?
№8. Имеется 10 различных книг и 15 различных журналов. Сколькими способами можно составить посылку из 3 книг и 5 журналов?
№9. В группе 6 сильных математиков. Сколькими способами из них можно составить команду для участия в районной олимпиаде, если от класса можно послать команду от 2 до 4 человек?
№10. Из 6 цветов краски, представленных в магазине, необходимо выбрать два различных цвета для стен в комнате и один, возможно, совпадающий с одним из них, для потолка. Сколькими способами это можно сделать?
Приложение № 23
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Элементы теории вероятностей»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 15 §5-11;
А.А.Дадаян «Сборник задач по математике», глава15 §1;
и конспекты учебных занятий и выполните следующие задания:
Задание 1.Ответьте на вопросы:
Что называется опытом или испытанием?
Что называется событием, случайным, достоверным и невозможным событием?
Какие события называют совместными и несовместными?
Какие события называют противоположными?
Что называют полной группой событий?
Сформулируйте теорему сложения двух несовместных событий.
Сформулируйте теорему умножения двух независимых событий.
Что называется условной вероятностью?
Запишите формулу полной вероятности. Запишите формулу Байеса.
Запишите формулу Бернулли.
Задание 2. Решите задачи:
№1. Какова вероятность того, что наугад выбранное целое число от 40 до 70 является кратным 6?
№2. Какова вероятность того, что при 5 подбрасываниях монеты она 3 раза упадет гербом кверху?
№3. В НИИ работает 120 человек, из них 70 знают английский язык, 60-немецкий, а 50-знают оба. Какова вероятность того, что выбранный наугад сотрудник не знает ни одного иностранного языка?
№4. Группа туристов, состоящая из 12 юношей и 8 девушек, выбирают по жребию хозяйственную команду в составе 4 человек. Какова вероятность того, что в числе выбранных окажется две девушки и два юноши?
№5. Два станка работают независимо друг от друга, причем вероятность бесперебойной работы первого станка в течение определенного времени равна 0,8, а второго- 0,85. Какова вероятность бесперебойной работы обоих станков в течение данного промежутка времени?
№6. В ящике находятся детали, из которых 12 изготовлены на первом станке, 20- на втором и 16- на третьем. Вероятность того, что детали, изготовленные на первом, втором и третьем станках стандартные, соответственно равны 0,9; 0,8 и 0,6. Найти вероятность того, что взятая наугад деталь окажется стандартной.
№7. Наудачу выбрана семья, имеющая пять детей. Вероятность рождения одного мальчика равна 0,5. Найти вероятность того, что в этой семье число мальчиков:
а) равно четырем;
б) не менее четырех;
в) не менее трех и не более четырех;
г) не менее трех;
д) хотя бы один.
№8. Вероятность попадания в мишень при одном выстреле равна 0,8. Произведено 100 выстрелов. Найти вероятность того, что мишень будет поражена:
а) ровно 85 раз; б) не менее 70 и не более 85 раз; в) не менее 85 раз; г) менее 85 раз.
Приложение № 24
САМОСТОЯТЕЛЬНАЯ РАБОТА
по теме: «Элементы математической статистики»
Повторите имеющийся материал по заданной теме, используя учебники:
А.А.Дадаян «Математика», глава 15 §12-15;
А.А.Дадаян «Сборник задач по математике», глава15 §6;
и конспекты учебных занятий и выполните следующие задания:
Задание 1.Ответьте на вопросы:
Что называется случайной величиной?
Что называется дискретной случайной величиной; непрерывной случайной величиной? Приведите примеры.
Что такое закон распределения случайной величины?
Что называется математическим ожиданием случайной величины?
Что называется дисперсией случайной величины?
Что называется средним квадратичным отклонением случайной величины?
Запишите неравенство Чебышева.
Сформулируйте теорему Чебышева (закон больших чисел).
Задание 2. Решите задачи:
№1. В учебной группе 25 студентов. Ниже приведены оценки, полученные этими студентами на экзамене по математике: 3;3;2;4;4;3;3;3;3;2;3;5;4;3;3;3;2;4;5;3;3;3;2;3;3. Составить статистическое распределение выборки, найти математическое ожидание, моду вариационного ряда и построить полигон частот статистического распределения.
№2. Получена выборка результатов измерения роста студентов-юношей, обучающихся на втором курсе (см): 179;167;181;183;166;177;173;178;164;172;169;177;173;176; 172;174;162;176;
173;179;181;166;182;161;167;174;171;181;175;175;186;176;176;165;173;174;172;170;170;173;172;176;174;174;170;178;185;183;172;176;180.
Составить интервальное распределение выборки с числом частичных интервалов, равным 5, и построить гистограмму частот статистического распределения.
№3. В результате измерения некоторой физической величины одним прибором получены следующие результаты: 11;12;15;20;22;18;17;21. Найти выборочную среднюю и выборочную дисперсию измерений.
№4. Найти доверительный интервал для оценки с надежностью 0,99 неизвестной генеральной средней в случае нормального распределения генеральной совокупности, если среднее квадратичное отклонение равно 3, выборочная средняя равна 5, объем выборки равен 36.
№5. Производятся последовательные независимые испытания пяти приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Построить ряд распределения случайного числа испытанных приборов, если вероятность выдержать испытания для каждого прибора равна 0,9.
Учебно-исследовательская работа по теме «Средние значения и их применение в статистике»
Литература:
(основная)
1. Дадаян А.А. Математика.- М.: «Форум», 2009.
2. Дадаян А.А. Сборник практических заданий по математике.- М.:«Форум»,
2009.
Дополнительная литература:
1.Башмаков М.И. Математика (базовый уровень). 10-11 кл. – М., 2005.
2.Башмаков М.И. Математика: 10-11 кл. Сборник задач по математике – М.,
2004.
3.Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа,
1990
4.Гусев В.А., Григорьев С.Г, Иволгина С.В. Математика.- М.: «Академия»,
2008
5.Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.
6.Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.
7.Луканкин Г.Л., Луканкин А.Г. Математика.– М., 2004.
8.Пехлецкий И.Д. Математика.– М., 2003.
Интернет-ресурсы:
http://mathworld.ru
http://www.exponenta.ru
http://www.mathtree.ru






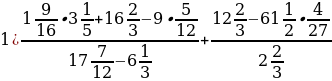
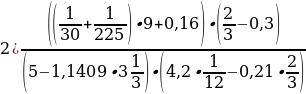
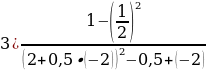
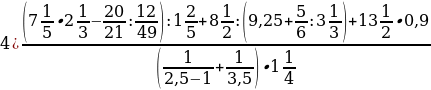
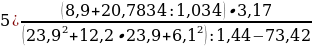
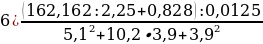
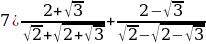
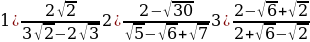
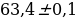 ; ВС=
; ВС=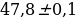 ; СА=
; СА=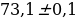 .
.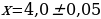 и длины
и длины 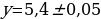 .
.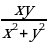 ,если
,если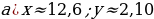
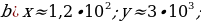
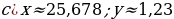
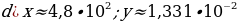
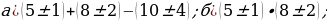
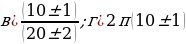
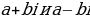 называются…
называются…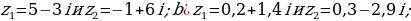
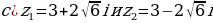
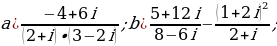
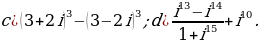
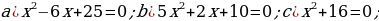
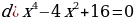 .
.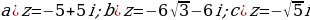
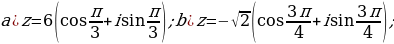
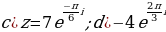
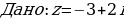 . Найдите
. Найдите 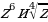 .
.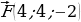 и углы, которые вектор
и углы, которые вектор 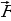 образует с осями координат.
образует с осями координат.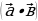 , если
, если 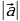 = 8,
= 8, 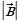 = 5 и
= 5 и 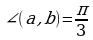 .
.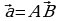 , если точки А и В имеют следующие координаты:
, если точки А и В имеют следующие координаты: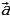 (3; 2;-3) и
(3; 2;-3) и 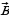 (-2; 6;-1). Найдите векторы:
(-2; 6;-1). Найдите векторы: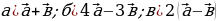
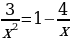 ; 3) 6х2 – х – 1 = 0;
; 3) 6х2 – х – 1 = 0;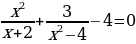 ;
;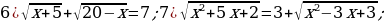
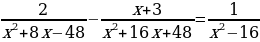
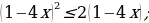 3) – х2 + 8х – 15 0;
3) – х2 + 8х – 15 0;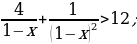 5)
5) 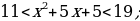 6)
6) 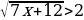 .
.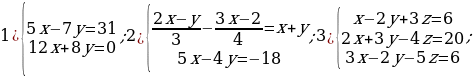
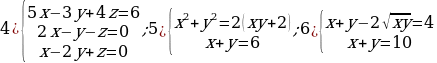
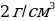 и
и 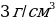 соответственно, составлена смесь. Сколько граммов взято каждой жидкости и каков удельный вес смеси, если 4
соответственно, составлена смесь. Сколько граммов взято каждой жидкости и каков удельный вес смеси, если 4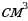 смеси весит в 10 раз меньше, чем вся вторая жидкость, а 50
смеси весит в 10 раз меньше, чем вся вторая жидкость, а 50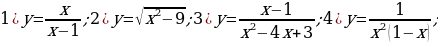
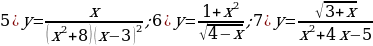
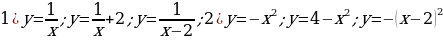
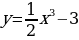 ; 2)
; 2) 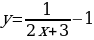 ;
; 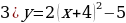
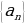 , если …
, если …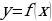 . Если аргумент х, изменяясь, стремится к некоторому числу а и при этом значение функции неограниченно приближается к числу А, тогда говорят, что…
. Если аргумент х, изменяясь, стремится к некоторому числу а и при этом значение функции неограниченно приближается к числу А, тогда говорят, что…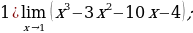
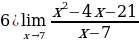
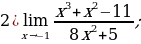
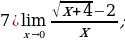
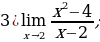
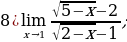
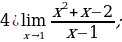
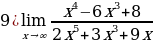
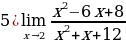
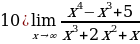
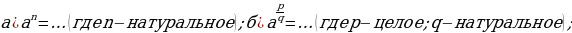

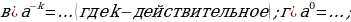
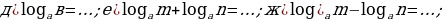
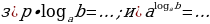
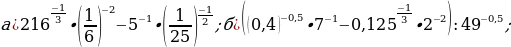
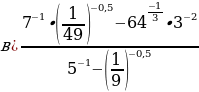
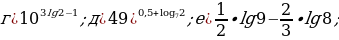
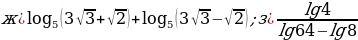
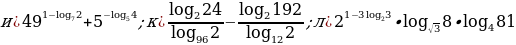
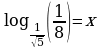 2)
2) 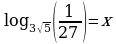 3)
3) 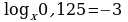 4)
4) 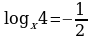
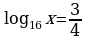 6)
6) 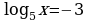 7)
7) 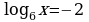 8)
8) 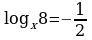
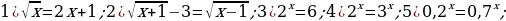
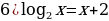
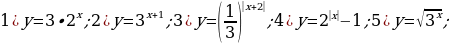
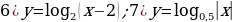
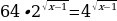
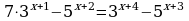
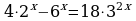
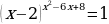
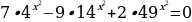
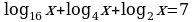
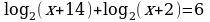
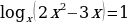
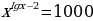
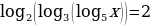
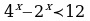 3)
3) 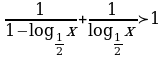
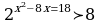 4)
4) 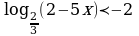
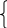
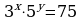 2)
2) 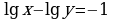
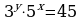
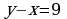
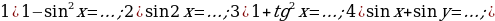
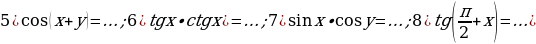
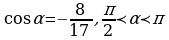
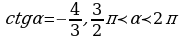
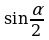 ,
, 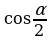 ,
, 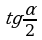 , если
, если 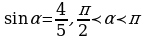
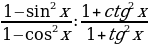
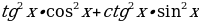
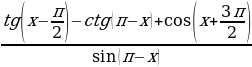
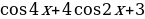
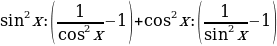
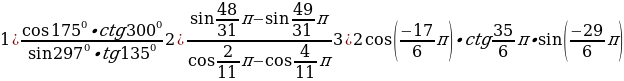
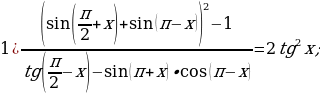
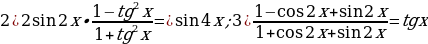
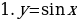
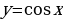
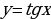
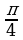 ); y = 3sin(x-
); y = 3sin(x-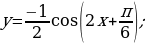
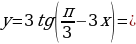
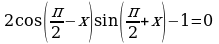
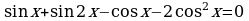
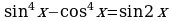
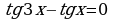

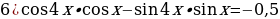
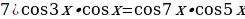
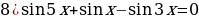
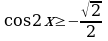
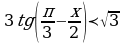
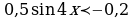
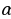
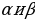
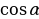 , если АВ=24м, АС=13м, АД=37м, СД=35м.
, если АВ=24м, АС=13м, АД=37м, СД=35м.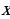 называется …
называется …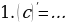
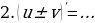
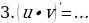
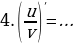
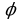 (x)) равна произведению …:
(x)) равна произведению …: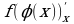 … .
… .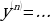
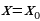 равна …
равна …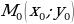 имеет вид…
имеет вид…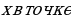
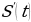 есть… ,а
есть… ,а 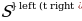 - …
- …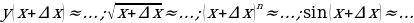
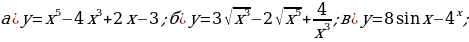
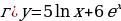 .
.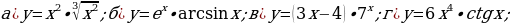
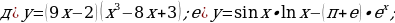
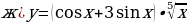 .
.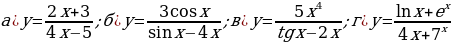 .
.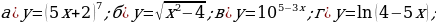
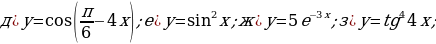
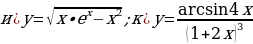 .
.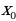 :
: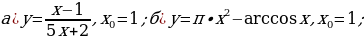
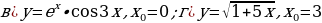 .
.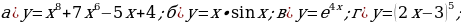
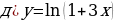 .
.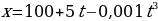 . Найдите
. Найдите 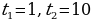 .
.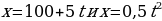 .
.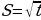 , то его
, то его 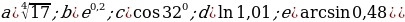
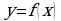 , имеющая на некотором промежутке
, имеющая на некотором промежутке 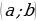 производную
производную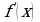 , возрастала на этом промежутке, необходимо и достаточно, чтобы для всех
, возрастала на этом промежутке, необходимо и достаточно, чтобы для всех 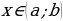 выполнялось неравенство
выполнялось неравенство 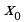 . Если
. Если 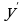 …; б) либо
…; б) либо 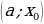 ,
, 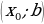 , тогда:
, тогда: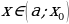 и б)
и б) 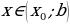
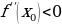 , то х0- точка … функции y=f(x), если
, то х0- точка … функции y=f(x), если 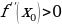 , то х0- точка … функции.
, то х0- точка … функции. .
.
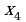
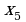
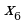
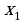 0
0 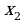
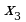
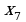
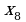
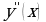 и
и 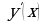 в отмеченных точках:
в отмеченных точках: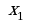
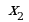
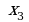
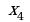
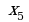
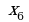
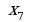
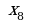
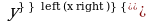
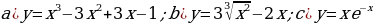
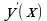 .
.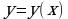 .
. 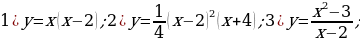
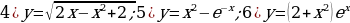
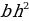 , где -основание прямоугольника в сечении балки,
, где -основание прямоугольника в сечении балки, 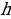 - его высота)
- его высота)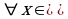 [a; b] справедливо равенство ... .
[a; b] справедливо равенство ... .
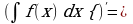 … .
… .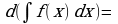 … .
… .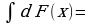 … .
… .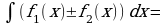 … .
… . … .
… .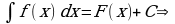
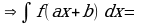 … .
… .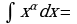 …
…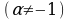
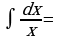 … .
… .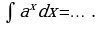
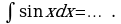
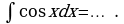
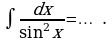
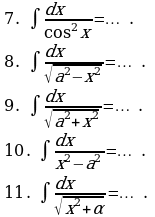
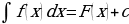 , тогда
, тогда 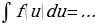 , где u(x) – произвольная дифференцируемая функция от х.
, где u(x) – произвольная дифференцируемая функция от х.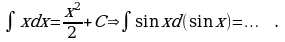
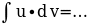
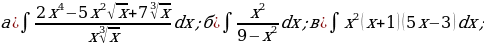
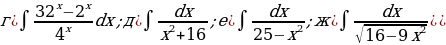
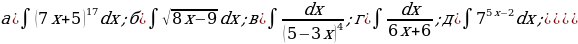
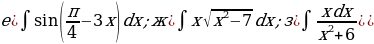
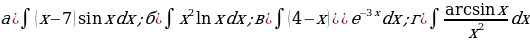
 , таких, что
, таких, что 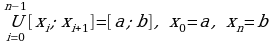 .
. 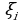 и для каждого значения i вычислено
и для каждого значения i вычислено 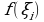 .
. 
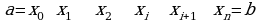 x
x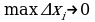 и при любом выборе точки
и при любом выборе точки 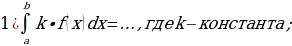
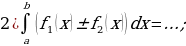
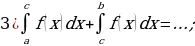
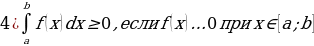
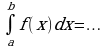
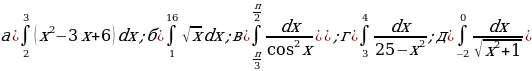
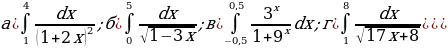
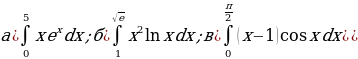
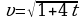 м/с. Найдите путь, пройденный точкой за первые 10 с от начала движения.
м/с. Найдите путь, пройденный точкой за первые 10 с от начала движения.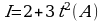 . Найти количество электричества, протекшее через поперечное сечение проводника за время от
. Найти количество электричества, протекшее через поперечное сечение проводника за время от 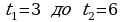 с.
с. 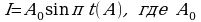 - его амплитуда. Найдите количество электричества, протекшего через поперечное сечение проводника за время от
- его амплитуда. Найдите количество электричества, протекшего через поперечное сечение проводника за время от 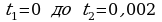 с.
с.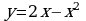 и прямой y = - x;
и прямой y = - x;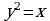 , гиперболой xy = 8 и отрезком прямой, соединяющим точку (8; 1) гиперболы с точкой
, гиперболой xy = 8 и отрезком прямой, соединяющим точку (8; 1) гиперболы с точкой 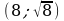 параболы;
параболы;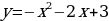 , осями координат и прямой х=2;
, осями координат и прямой х=2;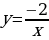 и прямыми х=1 и х=5.
и прямыми х=1 и х=5. 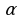 . Через гипотенузу проведена плоскость под углом
. Через гипотенузу проведена плоскость под углом 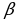 к плоскости основания. Эта плоскость пересекает боковое ребро призмы, выходящее из вершины прямого угла основания. Найдите площадь сечения.
к плоскости основания. Эта плоскость пересекает боковое ребро призмы, выходящее из вершины прямого угла основания. Найдите площадь сечения. 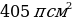 . Высота усеченного конуса в два раза меньше высоты соответствующего полного конуса. Вычислить объем усеченного конуса.
. Высота усеченного конуса в два раза меньше высоты соответствующего полного конуса. Вычислить объем усеченного конуса.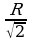 . Найдите объем этого цилиндра.
. Найдите объем этого цилиндра.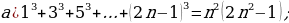
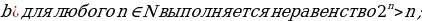
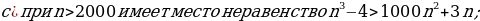
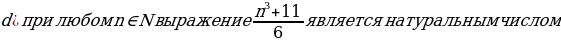 .
.









