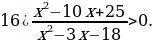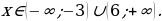| МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное АВТОНОМНОЕ образовательное учреждение высшего образования «Национальный исследовательский ядерный университет «МИФИ» |
| Московский областной политехнический колледж– филиал федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский ядерный университет «МИФИ» (МОПК НИЯУ МИФИ) |
Методическое пособие для студентов
«Непрерывность функции в точке и на множестве.
Решение неравенств методом интервалов».
Рассмотрено на заседании ПЦК
физико-математических дисциплин
Протокол № ____ от «____» ____________ 2021 г.
Председатель ЦК Л.А. Кувшинова___________
Разработал преподаватель математики
Е.Н. Лебедева ______________________________
г. Электросталь 2021 г.
Пояснительная записка
Настоящее пособие предназначено для студентов как дневных, так и заочных отделений колледжа, а также может быть использовано для самостоятельного изучения темы, овладения способами и методами решения задач в объеме действующей программы по математике для средних профессиональных учебных заведений.
Целью и основными задачами данной разработки являются пополнение знаний студентов основами математических знаний, умений и навыков в объеме, необходимом для их повседневной практической деятельности, для дальнейшей учебы и работы по специальности, для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путем самообразования, обеспечение выпускнику конкурентоспособности на рынке труда.
Изучение темы «Непрерывность функции в точке и на множестве. Решение неравенств методом интервалов» направлено на развитие гибкости мышления студентов, на привитие алгоритмической культуры.
Решение задач по математике у студентов колледжей часто сопряжено со многими трудностями. Помочь студентам преодолевать эти трудности, научить применять теоретические знания к решению задач – основное назначение настоящего пособия.
Пособие содержит программный материал. В данном пособии весь теоретический материал изложен кратко и, поэтому доступен для большинства учащихся. Это способствует решению важной педагогической задачи – научить работать с источником.
В работе представлены теоретические сведения, необходимые для усвоения материала и решения задач.
В пособии дан алгоритм решения типовых задач. Алгоритм – это совокупность четко определенных правил решения задач за конечное число шагов или последовательность выполняемых действий. Алгоритмы развивают логику, являются основой составления программ в работе с компьютером; алгоритмы используются в любой сфере деятельности человека.
Особенностью представленного пособия является усиление роли самостоятельной работы студентов.
Изучив, данное пособие студент должен уметь обобщать полученные знания, решать неравенства, используя метод интервалов.
Непрерывность функции в точке.
Р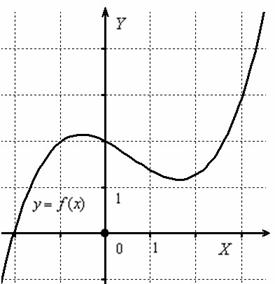 ассмотрим некоторую функцию
ассмотрим некоторую функцию 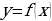 , непрерывную на всей числовой прямой:
, непрерывную на всей числовой прямой:
Или, говоря лаконичнее, наша функция непрерывна на 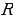 (множестве действительных чисел).
(множестве действительных чисел).
Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.
При этом следует чётко отличать два простых понятия: область определения функции и непрерывность функции. В общем случае это не одно и то же. Например,
Д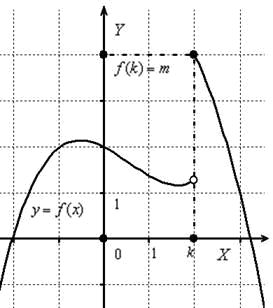 анная функция определена на всей числовой прямой, то есть для каждого значения
анная функция определена на всей числовой прямой, то есть для каждого значения 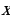 существует своё значение
существует своё значение 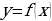 . В частности, если
. В частности, если 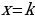 , то
, то 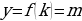 . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции:
. Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: 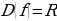 .
.
Однако. эта функция не является непрерывной на 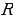 ! Совершенно очевидно, что в точке
! Совершенно очевидно, что в точке 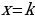 она терпит разрыв. Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги.
она терпит разрыв. Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги.
Определение: функция 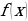 называется непрерывна в точке
называется непрерывна в точке 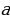 , если предел функции в данной точке равен значению функции в этой точке
, если предел функции в данной точке равен значению функции в этой точке
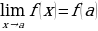 .
.
Из этого определения следует выполнение следующих условий:
1) Функция должна быть определена в точке 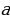 , то есть должно существовать значение
, то есть должно существовать значение 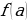 ;
;
2) Должен существовать предел функции 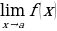 ;
;
3) Предел функции в данной точке должен быть равен значению функции в этой точке: 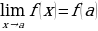 .
.
Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке 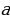 .
.
Свойства непрерывных функций:
Если функции 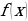 и
и  непрерывны в точке
непрерывны в точке 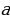 , то их сумма,
, то их сумма, 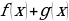 произведение
произведение 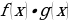 и частное
и частное 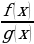 (если в знаменателе значение функции отлично от нуля) есть функция непрерывная в точке
(если в знаменателе значение функции отлично от нуля) есть функция непрерывная в точке 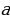 ;
;
Всякая рациональная функция непрерывна во всех точках, в которых она определена.
Непрерывность функции на множестве.
Определение. Функция 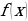 называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
Теорема. Если функция 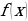 непрерывна на отрезке
непрерывна на отрезке 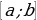 и на концах этого отрезка принимает значения разных знаков, то внутри этого отрезка найдется хотя бы одна точка в которой данная функция
и на концах этого отрезка принимает значения разных знаков, то внутри этого отрезка найдется хотя бы одна точка в которой данная функция 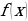 обращается в ноль.
обращается в ноль.
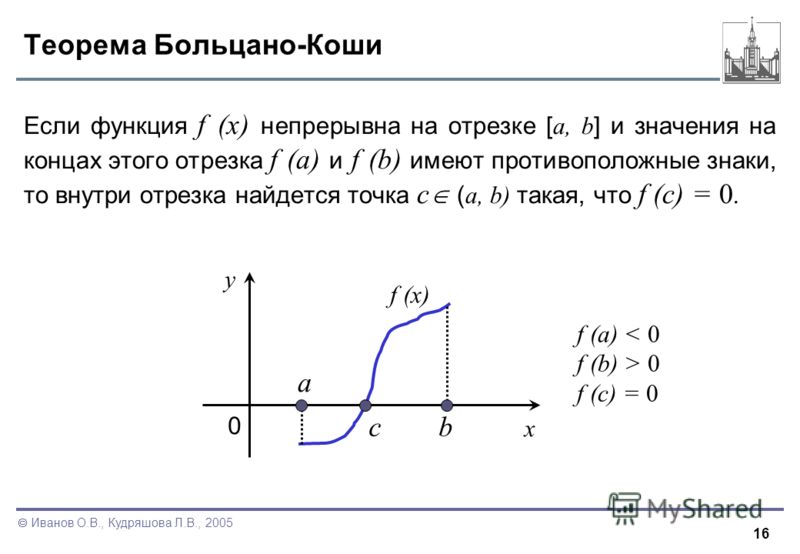
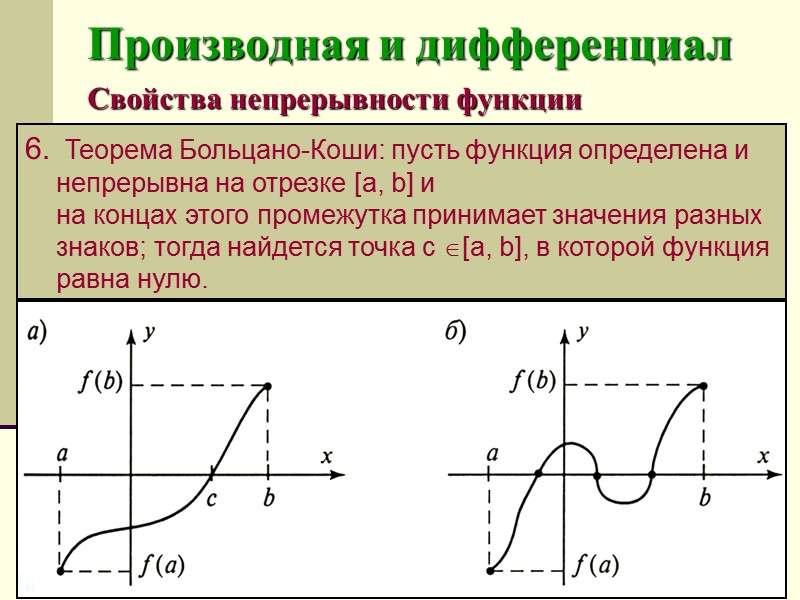
Геометрически это означает, что график функции пересекает ось  хотя бы один раз.
хотя бы один раз.
На факте этой теоремы основан метод решения неравенств с одной переменной, который называется методом интервалов.
Решение неравенств методом интервалов.
Пусть функция 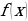 непрерывна на некотором промежутке и обращается в ноль в конечном числе точек этого промежутка. Этими точками этот промежуток разбивается на интервалы, в каждом из которых функция
непрерывна на некотором промежутке и обращается в ноль в конечном числе точек этого промежутка. Этими точками этот промежуток разбивается на интервалы, в каждом из которых функция 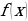 сохраняет постоянный знак.
сохраняет постоянный знак.
Чтобы определить знак неравенства достаточно вычислить значение функции 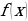 в какой либо точке каждого интервала.
в какой либо точке каждого интервала.
Алгоритм решения нелинейных неравенств:
Для начала необходимо привести неравенство к виду 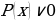 , где
, где 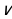 – знак неравенства , ≤ или ≥. Для этого необходимо перенести все слагаемые в левую часть неравенства;
– знак неравенства , ≤ или ≥. Для этого необходимо перенести все слагаемые в левую часть неравенства;
Найти корни получившегося выражения. Для этого надо решить уравнение 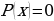 . Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Разложить левую часть неравенства на множители;
Одинаковые множители записать в виде степени (Внимание! Это действие необходимо сделать, чтобы не ошибиться с кратностью корней – если в результате получится множитель в четной степени, значит, соответствующий корень имеет четную кратность);
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов, в каждом из которых сохраняется постоянный знак;
Выяснить знак (плюс или минус) на самом правом интервале. Для этого достаточно подставить в 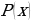 любое число, которое будет правее всех отмеченных корней;
любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. Исключения составляют неравенства, имеющие корни четной кратности. Важно! При переходе через точку, обозначающую корень четной кратности знак НЕ МЕНЯЕТСЯ.
Записать ответ.
Чертеж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать масштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами 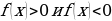 мы будем использовать обозначение точки в виде круга с выколотым (пустым) центром. В случае нестрогих неравенств
мы будем использовать обозначение точки в виде круга с выколотым (пустым) центром. В случае нестрогих неравенств 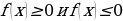 точки, которые соответствуют нулям в знаменателе (если дана рациональная функция) мы будем изображать выколотыми, а все остальные обычными черными.
точки, которые соответствуют нулям в знаменателе (если дана рациональная функция) мы будем изображать выколотыми, а все остальные обычными черными.
Рассмотрим, как решать неравенства методом интервалов, на конкретных примерах.
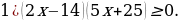
Решение.
Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:

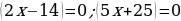
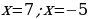
Полученные точки отмечаем на числовой прямой:
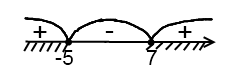
Для проверки знака берем 10 (из крайнего левого интервала). Подставляем 10 в данное неравенство, получим  . Таким образом, крайний левый интервал, из которого взяли 10, ставим знак «+» остальные знаки чередуем. Поскольку решаем неравенство нестрогое, то точки – закрашенные, выбираем промежутки со знаком «+» (
. Таким образом, крайний левый интервал, из которого взяли 10, ставим знак «+» остальные знаки чередуем. Поскольку решаем неравенство нестрогое, то точки – закрашенные, выбираем промежутки со знаком «+» (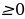 ) и записываем ответ.
) и записываем ответ.
Ответ: 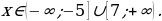
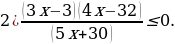
Решение.
П
 риравниваем к нулю левую часть:
риравниваем к нулю левую часть:

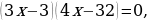
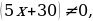
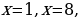

Полученные точки отмечаем на числовой прямой:
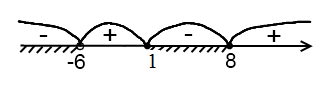
Для проверки знака берем 10 и подставляем его в данное неравенство. По знакам получаем:
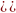
В промежуток, которому принадлежит 10, ставим «+», остальные знаки чередуем. Нам нужен «–», заштриховываем соответствующий промежуток. (Не забываем, когда точки закрашенные, а когда – выколотые. Те точки, в которых знаменатель обращается в нуль, выколотые всегда).
Ответ: 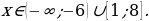
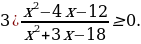
Решение.
П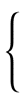
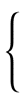 риравниваем к нулю левую часть:
риравниваем к нулю левую часть:
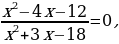
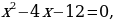
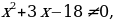
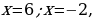
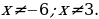
П олученные точки отмечаем на числовой прямой:
олученные точки отмечаем на числовой прямой:
Для определения знака берем 10 и подставляем его в данное неравенство.
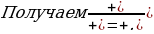
В промежуток, которому принадлежит 10, ставим «+», остальные знаки чередуем. Нам нужен «+», заштриховываем соответствующий промежуток. (Не забываем, когда точки закрашенные, а когда – выколотые и записываем ответ.
Ответ: 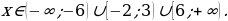
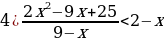
Переносим все слагаемые в левую часть, приводим к наименьшему общему знаменателю и упрощаем:
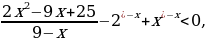
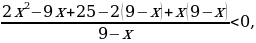
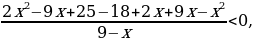
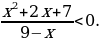
После упрощения решаем неравенство методом интервалов.
П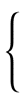
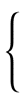 риравниваем к нулю левую часть:
риравниваем к нулю левую часть:
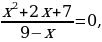
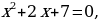
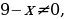
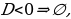
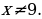
Т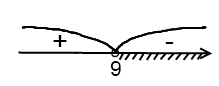 очек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку:
очек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку:
Для проверки берем 10. Подставляя его в последнее неравенство, получаем «–». На другом интервале – «+». Нам нужен интервал с «–».
Ответ: 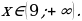
Рассмотрим решение неравенств, содержащих кратные корни четных степеней.
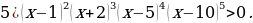
Решение.
Используем алгоритм решения неравенств методом интервалов. Приравниваем к нулю левую часть:
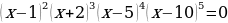
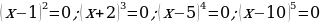
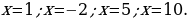
Полученные точки отмечаем на числовой прямой. Неравенство строгое, следовательно, все точки – выколотые. Корни 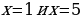 – кратные корни четной степени, поэтому в них – «петля»:
– кратные корни четной степени, поэтому в них – «петля»:
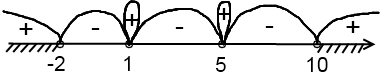
Для проверки знака берем 11 (из крайнего левого интервала) и подставляем его в данное неравенство. Получаем (+)∙(+)∙(+)∙(+), итого (+). Остальные знаки чередуем. Нам нужен знак «+», соответственно, выбираем промежутки с «+».
Ответ: 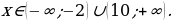
Рассмотрим еще три варианта решения этого же примера с разными знаками неравенства.
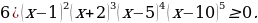
Решение.
В отличие от предыдущего примера, данное неравенство нестрогое, поэтому точки в этом случае – закрашенные:

Отдельно стоящие закрашенные точки включаем в решение!
Ответ: 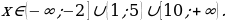
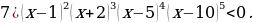
Решение.
Неравенство строгое, следовательно, точки и – выколотые. В этом неравенстве нам нужен знак «–»:
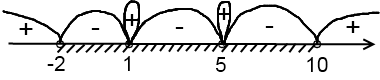
Ответ: 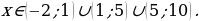
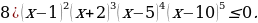
Решение.
От предыдущего неравенства это отличается только тем, что является нестрогим. Соответственно, точки в нем – закрашенные, и они входят в решение:
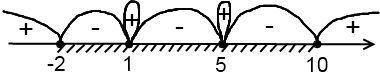
Ответ: 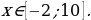
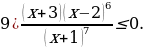
Решение.
Приравниваем к нулю левую часть:
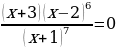
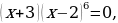
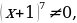
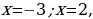

П
 олученные точки отмечаем на числовой прямой. Неравенство нестрогое, точки – закрашенные. Только точка, в которой знаменатель обращается в нуль, выколотая (всегда!).
олученные точки отмечаем на числовой прямой. Неравенство нестрогое, точки – закрашенные. Только точка, в которой знаменатель обращается в нуль, выколотая (всегда!).
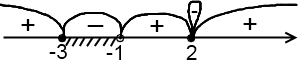
Для проверки знака берем 10. Подставляем его в данное неравенство. Получаем
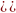
в итоге – «+». Нам нужен «–», заштриховываем соответствующий промежуток. Не забываем включить в ответ отдельно стоящую закрашенную точку.
Ответ: 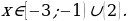
Рассмотрим примеры неравенств, в которых в ходе решения квадратного уравнения получаем дискриминант, равный нулю.
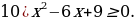
Решение.
Используем алгоритм решения неравенств методом интервалов. Приравниваем к нулю левую часть:
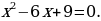
Найдем дискриминант:
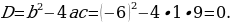
Поскольку дискриминант равен нулю, квадратное уравнение имеет один корень:
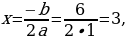
Т.е. левую часть данного неравенства можно представить в виде:
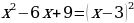 .
.
Корень 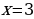 – кратный корень четной степени, поэтому на числовой прямой – «петля»:
– кратный корень четной степени, поэтому на числовой прямой – «петля»:
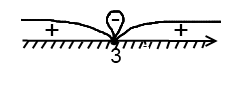
Неравенство нестрогое, точка – закрашенная. Знак неравенства 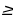 , поэтому нам нужны промежутки с «+» и не забываем включить в ответ закрашенную точку
, поэтому нам нужны промежутки с «+» и не забываем включить в ответ закрашенную точку 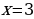 .
.
Ответ: 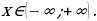
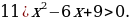
Решение.
От предыдущего неравенства это отличается только тем, что является строгим. Соответственно, точка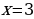 – выколотая, и в ответ ее не включаем:
– выколотая, и в ответ ее не включаем:
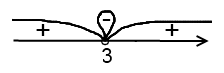
Ответ: 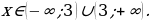
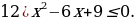
Решение.
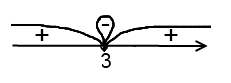
Поскольку знак неравенства 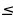 , то нам нужны промежутки со знаком
, то нам нужны промежутки со знаком
«–», а их нет. Отдельно стоящую закрашенную точку включаем в ответ. Здесь такая точка есть – 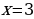 (напоминаю, знак в петле – «виртуальный», на самом деле при
(напоминаю, знак в петле – «виртуальный», на самом деле при 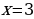 выражение, стоящее в правой части, равно нулю, а нуль не является ни положительным, ни отрицательным числом).
выражение, стоящее в правой части, равно нулю, а нуль не является ни положительным, ни отрицательным числом).
Ответ: 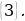
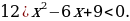
Решение.
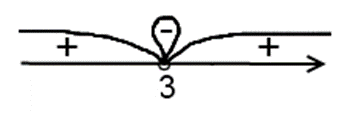
Здесь нет ни одной точки удовлетворяющей условию неравенства.
Ответ: 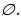
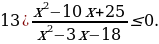
Решение.
П
 риравниваем к нулю левую часть. Получаем:
риравниваем к нулю левую часть. Получаем:
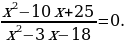
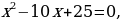
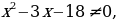
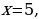
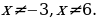
Поскольку в ходе решения уравнения 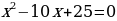 получили дискриминант, равный нулю, в соответствующей точке
получили дискриминант, равный нулю, в соответствующей точке 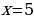 – «петля», т.к. это кратный корень. Отмечаем полученные точки на числовой прямой:
– «петля», т.к. это кратный корень. Отмечаем полученные точки на числовой прямой:
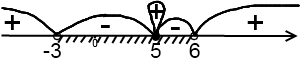
Знак неравенства 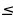 , поэтому выбираем промежутки со знаком «–». Точка
, поэтому выбираем промежутки со знаком «–». Точка 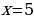 – закрашенная, поэтому ее включаем в ответ (то есть разрывать промежуток от –3 до 6 не нужно).
– закрашенная, поэтому ее включаем в ответ (то есть разрывать промежуток от –3 до 6 не нужно).
Ответ: 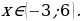
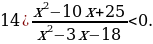
Решение.
О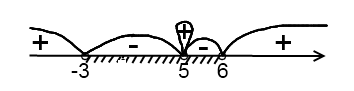 т предыдущего примера данный отличается только тем, что неравенство – строгое. Соответственно, все точки выколотые и точка
т предыдущего примера данный отличается только тем, что неравенство – строгое. Соответственно, все точки выколотые и точка 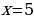 уже не входит в промежуток от –3 до 6 (промежуток от –3 до 6 разбивается на два промежутка).
уже не входит в промежуток от –3 до 6 (промежуток от –3 до 6 разбивается на два промежутка).
Ответ: 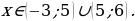
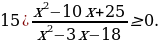
Р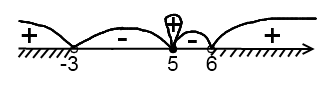 ешение.
ешение.
Здесь выбираем промежутки с «+». Отдельно стоящую закрашенную точку также включаем в ответ:
Ответ: 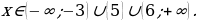
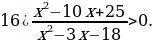
Решение.
Поскольку неравенство – строгое, ни одну из точек в ответ не включаем:
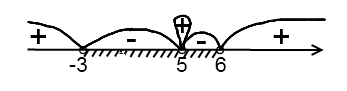
Ответ: 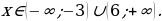
Следует заметить, что если бы мы решали квадратные уравнения, в которых дискриминант равен нулю, используя теорему Виета, то получили бы два одинаковых корня (то есть один и тот же корень встречается четное число раз). Если бы свернули квадратный трехчлен по формулам квадрата суммы или квадрата разности, то получили бы кратный корень четной степени. То есть, при любом подходе пришли бы к «петле».







 ассмотрим некоторую функцию
ассмотрим некоторую функцию 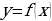 , непрерывную на всей числовой прямой:
, непрерывную на всей числовой прямой: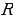 (множестве действительных чисел).
(множестве действительных чисел). анная функция определена на всей числовой прямой, то есть для каждого значения
анная функция определена на всей числовой прямой, то есть для каждого значения 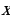 существует своё значение
существует своё значение 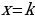 , то
, то 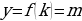 . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции:
. Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: 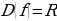 .
.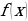 называется непрерывна в точке
называется непрерывна в точке 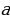 , если предел функции в данной точке равен значению функции в этой точке
, если предел функции в данной точке равен значению функции в этой точке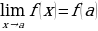 .
.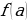 ;
;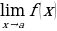 ;
; непрерывны в точке
непрерывны в точке 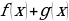 произведение
произведение 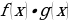 и частное
и частное 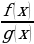 (если в знаменателе значение функции отлично от нуля) есть функция непрерывная в точке
(если в знаменателе значение функции отлично от нуля) есть функция непрерывная в точке 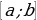 и на концах этого отрезка принимает значения разных знаков, то внутри этого отрезка найдется хотя бы одна точка в которой данная функция
и на концах этого отрезка принимает значения разных знаков, то внутри этого отрезка найдется хотя бы одна точка в которой данная функция 

 хотя бы один раз.
хотя бы один раз.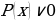 , где
, где 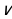 – знак неравенства , ≤ или ≥. Для этого необходимо перенести все слагаемые в левую часть неравенства;
– знак неравенства , ≤ или ≥. Для этого необходимо перенести все слагаемые в левую часть неравенства;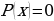 . Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;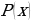 любое число, которое будет правее всех отмеченных корней;
любое число, которое будет правее всех отмеченных корней;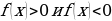 мы будем использовать обозначение точки в виде круга с выколотым (пустым) центром. В случае нестрогих неравенств
мы будем использовать обозначение точки в виде круга с выколотым (пустым) центром. В случае нестрогих неравенств 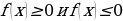 точки, которые соответствуют нулям в знаменателе (если дана рациональная функция) мы будем изображать выколотыми, а все остальные обычными черными.
точки, которые соответствуют нулям в знаменателе (если дана рациональная функция) мы будем изображать выколотыми, а все остальные обычными черными.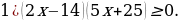

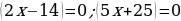
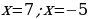

 . Таким образом, крайний левый интервал, из которого взяли 10, ставим знак «+» остальные знаки чередуем. Поскольку решаем неравенство нестрогое, то точки – закрашенные, выбираем промежутки со знаком «+» (
. Таким образом, крайний левый интервал, из которого взяли 10, ставим знак «+» остальные знаки чередуем. Поскольку решаем неравенство нестрогое, то точки – закрашенные, выбираем промежутки со знаком «+» (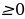 ) и записываем ответ.
) и записываем ответ.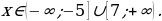
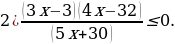

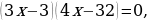
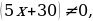
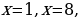


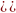
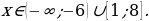
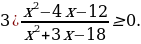
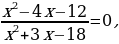
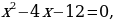
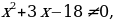
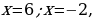
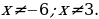
 олученные точки отмечаем на числовой прямой:
олученные точки отмечаем на числовой прямой: 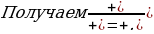
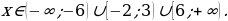
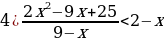
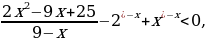
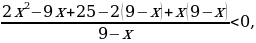
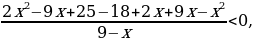
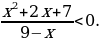
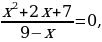
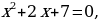
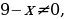
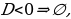
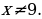
 очек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку:
очек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку: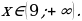
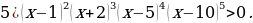
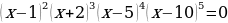
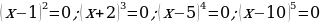
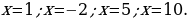
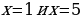 – кратные корни четной степени, поэтому в них – «петля»:
– кратные корни четной степени, поэтому в них – «петля»:
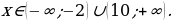
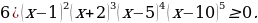

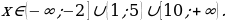
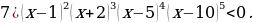

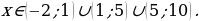
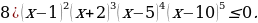

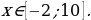
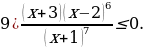
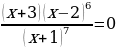
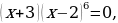
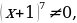
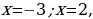


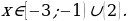
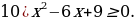
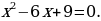
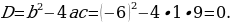
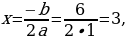
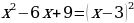 .
.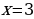 – кратный корень четной степени, поэтому на числовой прямой – «петля»:
– кратный корень четной степени, поэтому на числовой прямой – «петля»:
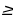 , поэтому нам нужны промежутки с «+» и не забываем включить в ответ закрашенную точку
, поэтому нам нужны промежутки с «+» и не забываем включить в ответ закрашенную точку 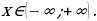
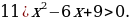

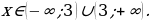
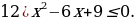

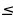 , то нам нужны промежутки со знаком
, то нам нужны промежутки со знаком 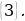
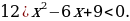

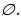
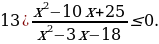
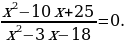
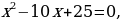
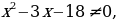
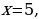
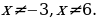
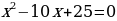 получили дискриминант, равный нулю, в соответствующей точке
получили дискриминант, равный нулю, в соответствующей точке 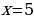 – «петля», т.к. это кратный корень. Отмечаем полученные точки на числовой прямой:
– «петля», т.к. это кратный корень. Отмечаем полученные точки на числовой прямой:
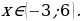
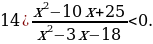
 т предыдущего примера данный отличается только тем, что неравенство – строгое. Соответственно, все точки выколотые и точка
т предыдущего примера данный отличается только тем, что неравенство – строгое. Соответственно, все точки выколотые и точка 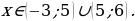
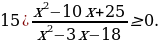
 ешение.
ешение.