Методы построения сечений многогранников

Климко В.П, учитель математики

«Методы построения сечений многогранников»

Если ученик в школе не научится сам ничего творить, то в жизни он всегда будет только подражать, копировать, т.к. мало таких, которые бы, научившись копировать, умели сделать самостоятельное приложение этих сведений.

Л. Н. Толстой. Актуальность темы.

Развитие школьника при изучении математики заключается в формировании у него характерных для этого предмета приёмов мыслительной деятельности. При этом с точки зрения воспитания творческой личности, особенно важно, чтобы в структуру умственной деятельности школьников помимо алгоритмических умений и навыков, зафиксированных в стандартных правилах, формулах и способах действий, вошли эвристические приёмы. Владение этими приёмами необходимо для самостоятельного управления процессом решения творческих задач, применения знаний в новых, необычных ситуациях.

Одной из главных целей преподавания геометрии как составной части математического образования принято считать формирование у школьников пространственных представлений. И это не столько внутренняя задача курса геометрии, сколько внешняя, связанная с подготовкой школьников к жизни, к труду в различных сферах общественно-полезной деятельности. Ориентация человека в пространстве является тем фундаментом, который необходим для практической деятельности по таким, например, специальностям, как архитектор, инженер, строитель, геодезист, чертежник, оператор, диспетчер, космонавт и т.п.

Способность создавать и оперировать пространственными образами характеризует уровень общего интеллектуального развития человека. В психологических исследованиях экспериментально подтверждено, что между склонностью учащихся к соответствующим профессиям и уровнем развития у них пространственных представлений имеет место статистически достоверная связь. Как внутренняя задача пространственные представления необходимы учащимся для восприятия учебного материала курса геометрии и для решения различного рода практических и теоретических задач. Но, несмотря на столь большую роль, которую играют пространственные представления, они сформированы у учащихся школ на крайне низком уровне. Об этом свидетельствуют и факты, и анализ изученной по этому вопросу литературы. Хочется отметить, что в пространственных представлениях следует различать две их стороны: создание пространственных образов и оперирование ими. Часто учащиеся испытывают большие трудности в оперировании образами, нежели в их создании. А в курсе изучении геометрии именно оперирование образами наиболее значимо в целях преобразования геометрических фигур. Оперирование образами, есть основное содержание пространственных представлений, и является критерием уровня их развития. Вот почему нужно обращать самое пристальное внимание на формирование у школьников умения оперировать образами.

В психологической литературе выделяют несколько типов оперирования пространственными образами:

а) образ подвергается преобразованиям, которые касаются изменения только его пространственного положения (мысленное вращение, перемещение уже созданного образа как в пределах одной плоскости, так и с выходом из нее);

б) образ подвергается преобразованиям, затрагивающим его структуру (мысленная перегруппировка составных элементов образа);

в) преобразования образа осуществляется и по пространственному расположению, и по его структуре одновременно и неоднократно.

Как показывают результаты анализа анкет, проводимых учёными среди учащихся старших классов, 14 % школьников имеют третий тип оперирования пространственными образами; 22,4 % - второй тип; 5,7 % - первый тип, а 58,9 % вообще не могут оперировать пространственными образами. Поэтому хотелось бы создать дидактическую систему изучения курса стереометрии (раздел «Построение сечений многогранников») в старших классах, позволяющую оптимизировать и повысить эффективность освоения школьниками учебного материала по разделу. Ведь если изучать разные методы построения сечений, то можно выработать способность не только создавать пространственные образы, но и легко ими оперировать. Поэтому выделю выделить следующие этапы работы:

• исследование и систематизация знаний о методах построения сечений;

• формирование умения выбора наиболее рационального метода;

• вывод учебного правила использования чертежа при решении;

• выяснение причин возникновения зрительных иллюзий;

• формирование рекомендаций для проведения занятий по данной теме.

Для этого постараюсь остановиться на вопросах дополнения и систематизации заданий изучения курса стереометрии (раздел «Построение сечений многогранников») в старших классах, позволяющую оптимизировать и повысить эффективность освоения школьниками учебного материала по разделу, пропаганде полученных знаний, которые так необходимы в старшей школе, умению применять полученные знания на практике, воспитание интереса к геометрии.

Изучение стереометрии есть благодатное условие для вооружения учащихся одним из богатейших средств познания окружающего мира – созданием и оперированием графическими образами трёхмерных объектов, что является фактором развития школьников. Переход от планиметрии к изучению стереометрии вызывает у учащихся большие трудности и связаны они с тем, что у школьников плохо развиты пространственные представления.

На первом этапе требуется определить уровень подготовленности учащихся к восприятию курса стереометрии. Выявить уровень подготовленности ребят к восприятию школьного курса стереометрии учителю помогут следующие тесты.

Тест №1

Пространственное мышление

( стандартное восприятие)

(можно проводить на уроке)

1. Внимательно прочитайте инструкцию. Время на работу с тестом равно 20 минут, поэтому не открывайте задание до тех пор, пока учитель не даст сигнал приступать к работе.

2. Вам будут предложены 30 рисунков, на которых изображены 15 кубов (каждый из них разрезан на две части), причём все «первые половинки» обозначены числами 1-15, а все «вторые половинки» обозначены (в другом порядке) буквами а – п.

Найдя пару для половинок 1 – 15, вы должны записать их буквами в таблице результатов под соответствующим номером.

Т А Б Л И Ц А Р Е З У Л Ь Т А Т О В

Тест № 2

Пространственное мышление

(продвинутый уровень)

Инструкция.

Представьте себе пространственную фигуру, сделанную из куска проволоки. Эта фигура не имеет двойных (накладывающихся на себя) участков и узлов, причём вся фигура целиком расположена внутри куба.

На уроках черчения Вы научились строить проекции таких фигур и тел.

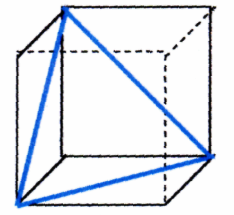
Тест, который предстоит Вам выполнить, предполагает обратные задания. Даны три проекции пространственной фигуры, и требуется схематически изобразить на чертеже куба, как выглядит эта фигура.

Например:

Дано: Требуется построить:

(искомое изображение

выделено жирной линией)

Таких заданий 12, и требуется выполнить как можно большее их число за 60 минут.

Роль чертежа в развитии пространственных представлений.

Важнейшим средством формирования у школьников пространственных представлений является чертёж. При решении стереометрических задач требования к качеству чертежа, его наглядности возрастают по сравнению с задачами планиметрическими. Первый и важнейший этап решения геометрической задачи всегда начинается с построения чертежа. Нельзя научиться решать достаточно содержательные геометрические задачи без прочных навыков по изготовлению "хороших" чертежей. Нужна привычка - не начинать решать задачи, пока не сделан "большой и красивый" чертеж, удовлетворяющий и математическим требованиям, и эстетическим критериям. И ещё - желательно научиться делать чертежи достаточно хорошего качества от руки, поскольку установка на использование чертёжных инструментов может сузить оперативный простор в процессе работы над решением.

Обучению учащихся умению изображать объемную фигуру плоскостным чертежом должно быть уделено самое пристальное внимание. Учащиеся должны знать, что для изображения объемной фигуры достаточно научиться изображать её отдельные точки, определяющие положение этой фигуры в пространстве. Полезно сообщить также некоторые свойства, которые необходимо учитывать при выполнении проекционных чертежей и различных построений, выполняемых на этих чертежах. В литературе определены следующие требования к оформлению чертежа, определяющие вид линий различного назначения. Укажем эти требования:

а) все части фигуры, данные по условию теоремы или задачи, должны изображаться линиями большей толщины, подходящей к размерам чертежа: толщина S основной линии берется от 0,6 мм до 1,4 мм;

б) все вспомогательные линии, проводимые при развитии доказательства теоремы или решении задачи, а также линии размерные и выносные берутся по толщине от S/3 до S/2 линии основного контура;

в) осевые линии изображаются штрих пунктиром толщиной от S/3 до S/2 основной линии;

г) в пространственных фигурах невидимые части изображаются штриховыми линиями: толщина их берется вдвое меньше сплошных линий соответствующего назначения;

д) для изображения плоских сечений пространственных фигур употребляется параллельная штриховка сплошными линиями; линии штриховки берутся толщиной от S/3 до S/2 основной линии. В плоских фигурах для выделения некоторых частей фигуры также может быть употреблена штриховка;

е) в курсе геометрии для указания равенства между собой двух отрезков можно перечеркивать их одинаковым числом штрихов. Равенство углов можно отмечать перечеркиванием их одинаковым числом дуг.

Необходимо научить учащихся относиться к чертежу критически, чему способствует учебное правило: "Не разрешается использовать в рассуждениях свойства фигуры, видимые на чертеже, если мы не можем обосновать их, опираясь на аксиомы и теоремы, доказанные ранее". Далее нужно сообщить учащимся причины возникновения зрительных иллюзий:

• глаз переоценивает величину острого и недооценивает величину тупого угла;

• темная фигура на светлом фоне кажется больше, чем равная ей светлая фигура, расположенная на темном фоне;

• глаз делает ошибку в определении размеров фигур в «заполненном» и в «пустом» пространстве;

• искажено восприятие направления, расстояния и формы фигуры под влиянием других, близко размещённых предметов и фигур.

Школьники привыкают работать с шаблонными изображениями геометрических фигур, а поэтому они часто оказываются беспомощными, когда им надо создать образ по чертежу, на котором пространственный объект расположен нетрадиционно. Поэтому целесообразно рассматривать различные изображения одного и того же тела. Например, различные изображения куба:

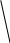
Формированию у ребят умений изображать плоскостным чертежом пространственные геометрические тела будут способствовать, например, такие задачи:

1. Анализируя изображение геометрической фигуры, ответьте на вопросы:

а) Какие фигуры изображены на рисунках?

б) Назовите видимые элементы фигур.

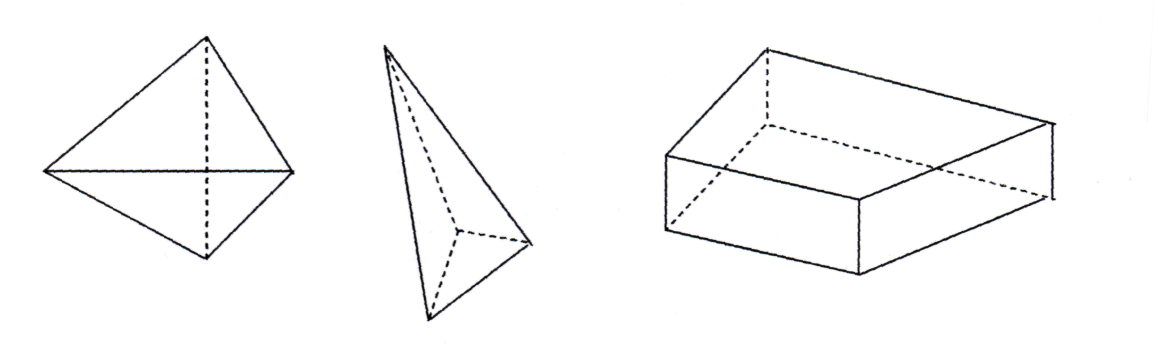
в) Какие плоские геометрические фигуры могут составлять поверхности изображенных фигур?

2. ABCDEKHO – изображение куба. Выпишите все изображенные на рисунке пирамиды и призмы, указывая вид фигуры.

3. Постройте изображение фигуры до:

а ) куба

б) треугольной пирамиды

в) четырёхугольной пирамиды

г) произвольного многоугольника

Итак, общие требования к чертежу можно выразить двумя словами: он должен быть верным и наглядным.

Методы изображения многогранников

Легче всего "поддаются" изображению многогранники, и, прежде всего, правильные треугольные и четырехугольные призмы и пирамиды. Рассмотрим некоторые моменты, связанные с изображением многогранников.

Всякий плоский предмет можно точно изобразить на бумаге, и здесь не возникает вопросов о каких-либо методах изображения (кроме только подобного изменения размеров). Если же требуется изобразить пространственный (трехмерный) предмет, то его нельзя точно скопировать. Исключим из рассмотрения изготовление моделей, копирующих оригинал. Этот процесс слишком сложен и может применяться лишь в исключительных случаях. В повседневной же практике мы вынуждены довольствоваться изображением пространственных тел на плоскости. Условимся о следующих терминах. Предмет, подлежащий воспроизведению, называется оригиналом.

Плоская фигура, воспроизводящая или представляющая оригинал, называется изображением. Совокупность правил, определяющих, каким образом, зная оригинал, получить его изображение, составляет метод изображения. Существует несколько различных методов изображения. К ним предъявляются требования наглядности и удобоизмеримости. Наглядность – это способность изображения вызывать зрительное впечатление, сходное с тем, какое вызывает оригинал. Изображение должно в некотором смысле заменить оригинал. Наглядность можно понимать и так: всякий человек, рассматривающий изображение должен понимать, что оно изображает. Для этого не требуется специальной подготовки или знания каких-нибудь условностей. Удобоизмеримость понимается так: по изображению можно, и притом несложно, восстановить оригинал как твердое тело, т.е. определить все его размеры. Инженерный рисунок обычно определяет оригинал, который должен быть изготовлен, например, здание, деталь машины и т.п. Ясно, что такой рисунок должен определять оригинал метрически точно. Требования наглядности и удобоизмеримости противоречат одно другому. При построении изображений, например, для художественных целей предпочтение отдается наглядности. Поэтому художники всегда пользуются методом изображения (он называется центральной проекцией), обеспечивающим наилучшую наглядность по сравнению с другими методами. Самое большое распространение имеют методы изображения, в которых достигнут некоторый компромисс между требованиями наглядности и удобоизмеримости, как, например, методы параллельной и центральной проекций.

Изображение фигуры.

Метод параллельного проектирования

Выберем некоторую плоскость π и назовем ее плоскостью изображений. Затем возьмем ненулевой вектор р, не параллельный плоскости π. Направление этого вектора назовем направлением проектирования. Пусть F – произвольная фигура, расположенная в пространстве (оригинал), а F' – параллельная проекция этой фигуры на плоскость π (проекция оригинала). Любую фигуру F на плоскость π, подобную фигуре F ' называют изображением фигуры F.

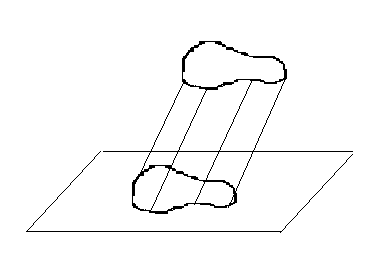
Д анная фигура

И зображение фигуры

Плоскость изображений.

Изображение фигуры зависит от выбора плоскости π, направления проектирования и выбранного подобия плоскости π. Обычно берется такое изображение, которое является наиболее наглядным.

Построение изображений фигур с помощью параллельного проектирования основано на:

1. основных свойствах параллельного проектирования;

2. аффинных отображениях;

3. теореме Польке-Шварца.

Основные свойства параллельного проектирования сформулированы в учебнике Л. С. Атанасяна, мы же остановимся на понятии аффинного отображения и сформулируем теорему Польке-Шварца. Введем понятие аффинного отображения одной плоскости на другую. Пусть π и σ - различные или совпадающие плоскости пространства. Взаимно однозначное отображение f : π → σ называется аффинным отображением плоскости π на плоскость σ, если оно любые три точки А, В, С плоскости π, лежащие на одной прямой, переводит в три точки А1, В1, С1 плоскости σ, лежащие на одной прямой, и сохраняет их простое отношение. В аффинном отображении одной плоскости на другую прямая переходит в прямую, параллельные прямые - в параллельные прямые, полуплоскость переходит в полуплоскость, луч - в луч, отрезок - в отрезок, угол - в угол. Из этого следует, что выпуклый (невыпуклый) многоугольник переходит в одноименный выпуклый (невыпуклый) многоугольник. Далее сформулируем теорему Польке-Шварца. «Если в пространстве задан произвольный тетраэдр АВСD и на плоскости начерчен любой полный четырехугольник А1В1С1D1, то существует такое положение тетраэдра перед плоскостью и такое направление проектирования, что тетраэдр, либо фигура, подобная ему, проектируется в начерченный полный четырехугольник».

То есть, всякий начерченный полный четырехугольник может служить изображением любого данного тетраэдра.

Из теоремы вытекают следствия:

1. произвольный чертеж тетраэдра соответствует в оригинале тетраэдру любой формы;

2. в изображении тетраэдра, так же как и в изображении треугольника, нельзя нарушать законы параллельных проекций.

Центральное проектирование.

Теория центральных проекций сложнее теории параллельных проекций. Центральная проекция строится следующим образом. Фиксируем в пространстве центр проекции S и плоскость проекции σ. Пусть М′ - любая точка пространства, отличная от S. Проводим прямую S М′ (проектирующая прямая); точка М ее пересечения с плоскостью σ считается изображением М′.

Центральную проекцию удобно рассматривать только в проективном пространстве, так как в нем всякая точка (кроме S) имеет изображение. При этом изображение собственной точки может оказаться несобственной точкой, а изображение несобственной точки может оказаться собственной точкой.

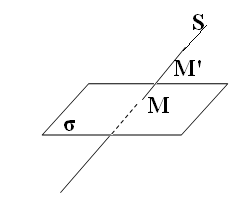
Центральные проекции обладают следующими свойствами:

каждой точке пространства, кроме центра проекции, однозначно соответствует точка на проективной плоскости σ;

прямая, если только она не проектирующая, изображается прямой; проектирующая прямая изображается точкой;

если точки A, B, C, D принадлежат одной прямой (не проектирующей), то

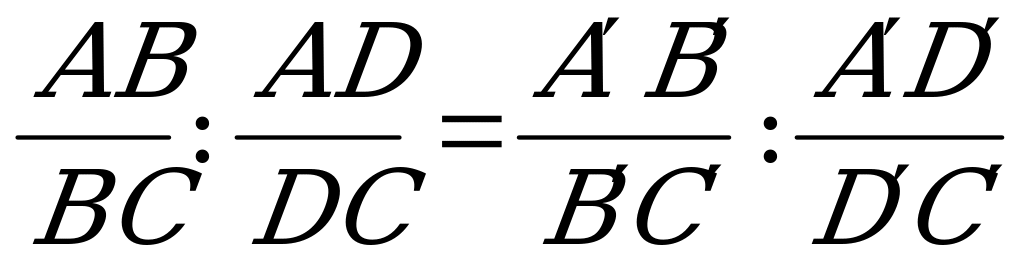
При центральном проектировании основная задача будет выглядеть так: точки А(А1), В(В1), С(С1) определяют плоскость. Требуется найти точку Х встречи плоскости АВС с данной проектирующей SP1.

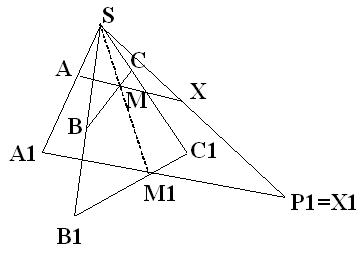
Так как основание Х1 точки Х должно совпадать с точкой Р1, то можем построить точку М1, как пересечение диагоналей четырехугольника А1В1С1Х1 и по ней найти точку М для четырехугольника-оригинала АВСХ.

М = ВС ∩ SМ1

Проведя АМ до пересечения с SР1, находим искомую точку Х.

Роль задач на построение сечений в школьном курсе стереометрии.

В школьном курсе стереометрии можно выделить два основных типа задач, связанных с многогранниками. Первый тип: задачи на вычисление элементов - длин, площадей, объемов, линейных и двугранных углов - указанных многогранников. Второй тип: задачи на сечения. В данной работе мне бы хотелось поговорить о роли задач на построение сечений многогранников, в немалой степени способствующих развитию пространственных представлений учащихся. Рассмотрим, как представлена тема "Построение сечений многогранников" в школьных учебниках по геометрии Л. С. Атанасяна и А.В. Погорелова. Решение задач на построение сечений у Атанасяна начинается в начале изучения курса стереометрии 10 класса в главе «Взаимное расположение прямых и плоскостей». Построение сечений производится на пространственных многогранниках: тетраэдре и параллелепипеде. Решение данных задач основывается на аксиомах стереометрии, теоремах и следствиях из них, изученных ранее. В учебнике под редакцией Погорелова данная тема изучается в 11 классе в главе «Многогранники». После введения понятий призмы и пирамиды переходят к построению плоских сечений данных фигур. Объяснение задач на построение сечений основано на методе следов. Однако этот метод более упрощен, т.к. след секущей плоскости на плоскости основания уже задан.

В подборе задач у Атанасяна есть:

1. задачи на построение сечений;

2. задачи на доказательство;

3. задачи на отношение площадей сечения и данной фигуры.

В учебнике Погорелова нет задач на доказательство, хотя ясно, что именно такие задачи позволяют комплексно проверить знания. В данном учебнике рассматриваются следующие задачи:

1. задачи на построение сечений (в большинстве случаев сечения строятся, опираясь на аксиомы стереометрии);

2. задачи на нахождение площади сечения.

В школьных учебниках геометрии рассматриваются задачи, в которых задания на построение сечений выступают не как цель обучения, а как средство обучения.

Как показал анализ учебной литературы, основными методами построения сечений в школьном курсе являются:

• нахождение линии пересечения двух плоскостей;

• нахождение точки пересечения прямой с плоскостью;

• построение прямой, параллельной данной плоскости;

• построение прямой, перпендикулярной плоскости.

Данные методы опираются на основные аксиомы стереометрии, теоремы, следствия из них. Таким образом, изучение основных понятий, аксиом и решение различного рода задач на подготовительном этапе способствуют развитию пространственных представлений и формируют достаточно знаний для изучения новых более сложных методов построения сечений. Уровень изложения материала по теме «Задачи на построение сечений» в школьных учебниках рассчитан на среднего ученика и не соответствует познавательным возможностям учащихся с хорошими способностями к изучению математики. В связи с этим, на мой взгляд, возникает необходимость введения новых более сложных методов построения сечений. Реализация этих требований возможна благодаря дифференцированному подходу к изучению данной темы. Это позволяет создать оптимальные условия для проявления способностей и интересов учащихся. Таким образом, содержание материала по теме " Задачи на построение сечений многогранников " в школьном курсе стереометрии следует дополнить изучением новых методов:

• методом следов;

• методом внутреннего проектирования;

• комбинированным методом.

Известно, что на изучение каждой темы, программой предусмотрено определенное количество часов, поэтому учитель должен сам решить, в какой форме лучше ознакомить ребят с новыми способами построения сечений. Это могут быть дополнительные программные часы, факультативные занятия; рассмотреть данные методы в классах с углубленным изучением математики и т.п.

Глава II

Обучение решению задач на построение сечений.

За основу была выбрана теория поэтапного формирования умственных действий и знаний. Руководствуясь этой теорией, изложение темы «Задачи на построение сечений» можно разбить на четыре этапа:

1. подготовительный этап;

2. ознакомительный этап;

3. формирующий этап;

4. совершенствующий этап.

Цель:

1. формирование умений построения сечений различными методами;

2. развитие пространственного мышления учащихся.

Рассмотрим каждый из выделенных этапов.

Подготовительный этап.

Работу над решением задач целесообразно готовить предварительными упражнениями. Упражнения являются важным средством формирования учебных умений и навыков. Содержание упражнений должно обеспечивать определенный уровень мыслительной деятельности учащегося, соответствующий дидактическим целям этапа, т.е. строится по принципу нарастания сложности. Целью подготовительных упражнений является глубокое осмысливание вопросов о взаимном расположении прямых и плоскостей в пространстве, способствующее формированию основных методов построения сечений.

Исходя из этого, содержание упражнений целесообразно разбить на четыре группы.

1. Диагностические задачи – задачи на актуализацию представлений об известных объектах. Цель – проверить, какой уровень у учащегося пространственных представлений.

Задача 1. Пересекаются ли прямые МС и РК?

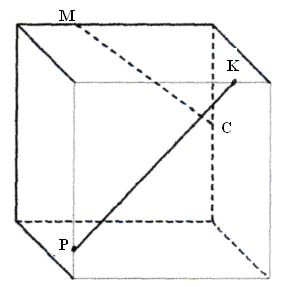
1. Конструктивные задачи – задачи, в процессе решения которых перед учащимися раскрываются предметно-материальные условия происхождения геометрических фигур.

Задача 2. На рисунке точки M, N, P – середины соответственно отрезков DA, DB, DC . Определить взаимное расположение прямых:

а) ND и AB; б) MP и AC в) PK и BC; г) KN и AC д) MN и AB; е) MD и BC.

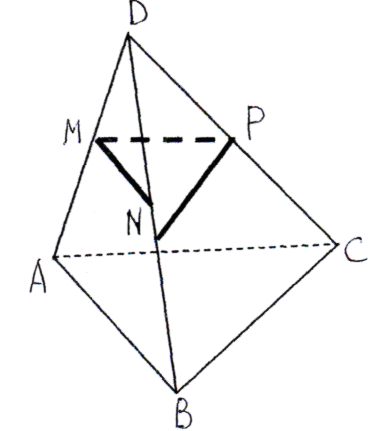1. Графические задачи – задачи на изображение геометрических фигур чертежами, а также на построение фигур по их характеристическим свойствам. Их цель – выявить ошибочные пространственные представления, причины их возникновения.

Задача 3. Найти точку пересечения прямой MN с плоскостью основания.

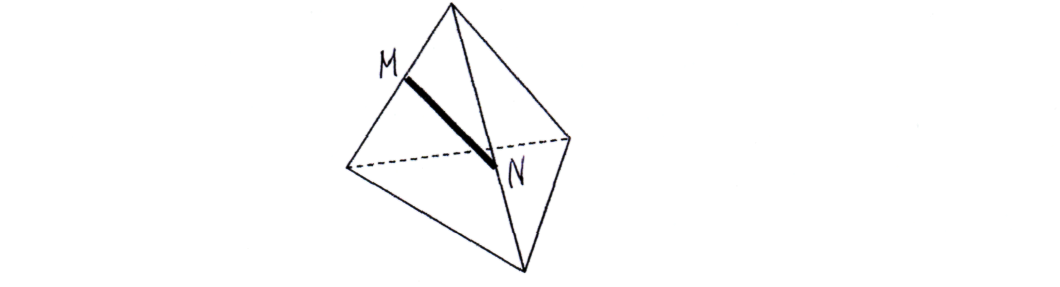
Задача 4. Точка А расположена на боковом ребре куба, точка В – на пересекающей это ребро стороне верхнего основания. Построить точку встречи прямой АВ с продолжением ребер куба.

1. Интегрирующие задачи – задачи, которые учат учащихся выделять те свойства объектов, которые позволяют отыскивать их среди множества других. Цель – выявить, как сформированы пространственные представления, их полнота, осознанность и правильность.

Задача 5. Пользуясь изображением параллелепипеда, установить взаимное расположение указанных в таблице прямых и плоскостей, при этом в клетках записать ответ словами: «параллельны», «скрещиваются», «пересекаются», «принадлежат».

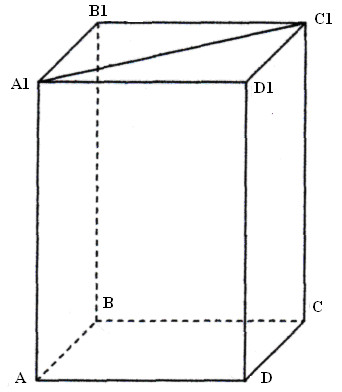
Элементы	СС1	DB	DD1C1C
АА1
ABCD

На данном этапе используются наглядные пособия, в частности, модели фигур. Упражнения предъявляются в виде устных задач на готовых чертежах, также в виде письменных задач. Данные подготовительные упражнения обеспечивают создание основы для решения задач на построение сечений.

Ознакомительный этап.

На данном этапе ставится следующая цель: формирование понятий секущей плоскости и сечения многогранника; ознакомление с методами построения сечений; развитие пространственных представлений при построении сечений данными методами.

Содержание разбито следующим образом:

1. Введение основных принципов построения простейших сечений.

2. Введение метода следов.

3. Введение метода внутреннего проектирования.

Ознакомительный этап начинается с изучения понятий секущей плоскости и сечения многогранника. Далее выполнить ряд заданий, например:

Упражнение 1. Точка М – середина ребра SA тетраэдра SABCD. Построить сечение плоскостью, проходящей через точку М, параллельно плоскости грани АВС.

Упражнение 2. Построить сечение через данные точки К,L, М.

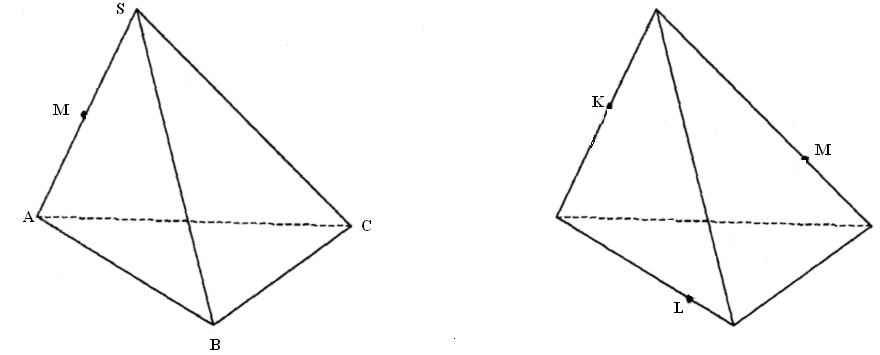
Анализируя решения всех задач, делается вывод: сечениями в тетраэдре могут быть только треугольники и четырехугольники, а в параллелепипеде – треугольники, четырехугольники, пятиугольники и шестиугольники.

Введение метода следов

Учащимся предлагаются следующие задания:

Упражнение 1. Найти точки пересечения прямой MN с плоскостью основания.

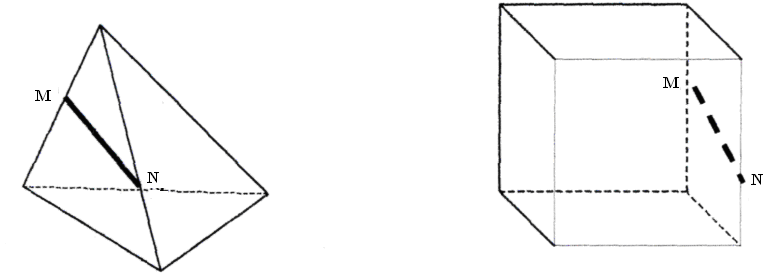
Упражнение 2. Построить сечение данного многогранника через данные точки M, N, K.

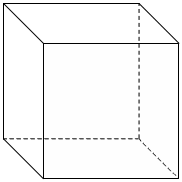
В ходе анализа и решения данной задачи выяснить, что при продолжении секущая плоскость будет пересекать плоскость основания. Таким образом, возникает проблема нахождения прямой, по которой секущая плоскость будет пересекать плоскость основания. Далее находят точки пересечения сторон секущей плоскости (при их продолжении) с плоскостью основания. Через данные точки строится искомая прямая. Проблема решена: прямая найдена и построена. Пользуясь полученным чертежом, вводится определение следа секущей плоскости, как прямой, полученной в результате пересечения секущей плоскости с плоскостью основания.

После рассмотрения понятия следа нужно выполнить следующее задание.

Упражнение 3. На грани многогранника известна точка К, принадлежащая сечению, и на плоскости основания задан след секущей плоскости. Построить прямую, которая является пересечением данной грани с секущей плоскостью.

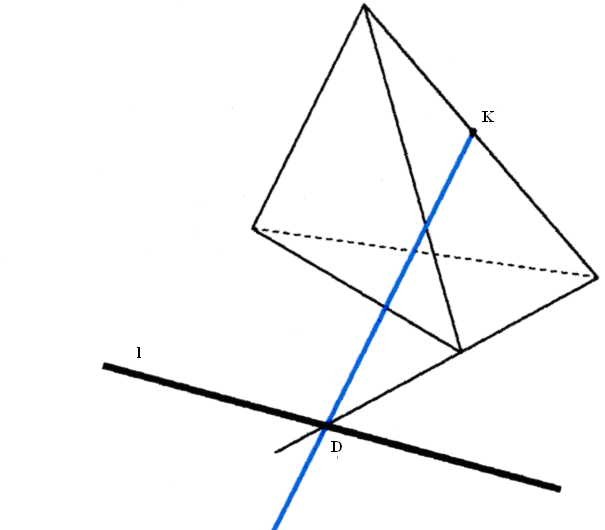
В ходе выполнения этого упражнения выделяются этапы решения данного задания:

1. строится пересечение следа с плоскостью грани (точка D);

2. полученная точка D соединяется с данной точкой К;

3. LM - искомая прямая.

Упражнение 4. Построить сечение через данную точку L на грани SB, если на плоскости основания задан след секущей плоскости.

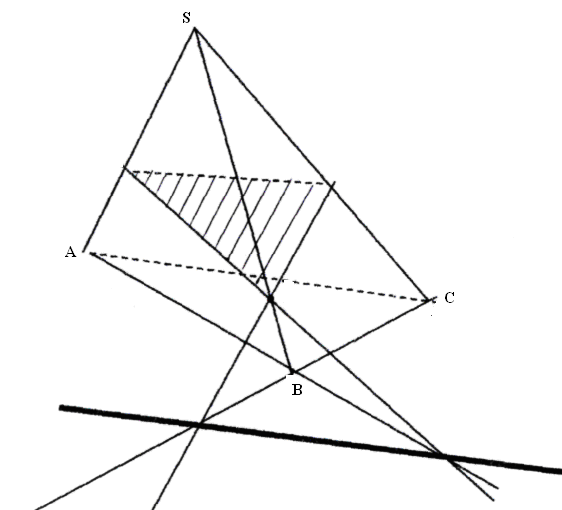
В ходе анализа и решения этой задачи обращается внимание на то, что, если заданы точки сечения и построен след секущей плоскости, то можно построить сечение.

Решение можно разбить на несколько этапов:

1. строится прямая пересечения секущей плоскости с плоскостью основания;

2. находятся точки встречи следа с плоскостями боковых граней;

3. полученные точки вместе с данными точками секущей плоскости определяют прямые искомого сечения.

С целью проверки осознанного усвоения данного метода можно выполнить задание:

Упражнение 5. С помощью метода следов построить сечение четырехугольной призмы через данные точки M, N, L.

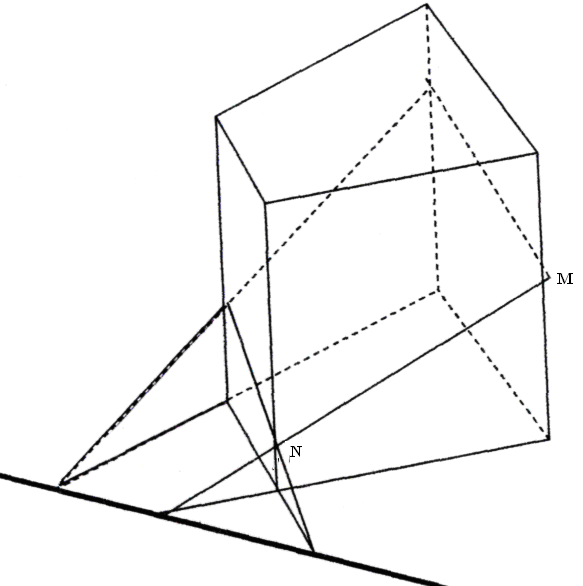
При изучении метода следов необходимо рассмотреть следующие группы задач:

1. построение сечений по трем данным точкам методом построения следа секущей плоскости на плоскости основания;

2. построение сечений плоскостью, заданной прямой (следом) и точкой К, заданной на ребре многогранника;

3. построение сечений плоскостью, заданной прямой (следом) и точкой К, заданной на грани многогранника;

4. построение сечений плоскостью, заданной прямой (следом) и точкой К, заданной внутри многогранника;

5. построение сечений плоскостью, заданной точкой К и прямой (следом), не пересекающей стороны основания многогранника;

6. построение сечений плоскостью, заданной точкой К и прямой (следом), пересекающей стороны основания многогранника;

7. построение сечений плоскостью, заданной точкой К и прямой (следом), совпадающей с одной из сторон основания многогранника.

Введение метода внутреннего проектирования.

Рассмотрение метода внутреннего проектирования можно начать с решения задачи: Усечь пирамиду SABCDE плоскостью, проходящей через данные точки M, K, N на ребрах пирамиды.

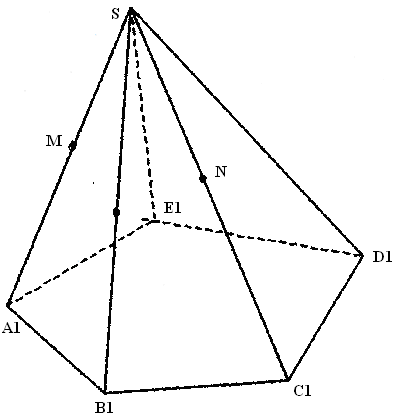
При построении сечения пирамиды известными методами учащиеся сталкиваются с проблемой нахождения точек пересечения прямых и плоскостей, т. к. некоторые из этих точек будут находиться за пределами листа тетради. Возникает вопрос: можно ли построить сечение в данном случае? Необходимо уяснить, что проекционный чертеж должен обладать полнотой, т.е. таким свойством, когда для любой изображенной на нем точки было определено ее основание. Необходимо убедиться, что при решении задач на построение сечений призмы мы будем пользоваться параллельным проектированием, а при построении сечения пирамиды – центральным проектированием. За центр проектирования выбираем вершину пирамиды.

Метод внутреннего проектирования.

Метод следов неудобен, когда точка пересечения прямой с плоскостью не попадает на лист бумаги, или построения занимают большую часть листа бумаги. В этом случае более удобен метод внутреннего проектирования.

Сущность этого метода заключается в нахождении по элементам сечения в многогранниках их проекций и обратно: по проекциям элементов сечения - самих элементов сечения. Приступая к выяснению нового способа построения сечений, необходимо обратить внимание на то, что в тексте задачи говорится, что на поверхности призмы (пирамиды) даны три точки, и перейти к выяснению понятия "заданные точки". Если принять, что проектирование идет параллельно ребру призмы, то легко для каждой данной точки найти ее проекцию на плоскости основания. Проекцию точки на основную плоскость будем называть "основанием" данной точки. Таким образом, будем считать заданными на изображении лишь те точки, для которых даны или могут быть построены на изображении соответствующие им основания. Анализируя данную задачу, можно сделать вывод, что любой точке искомого сечения будет соответствовать определенная точка основания. Эту точку мы получим, если из точки сечения проведем проектирующую прямую (параллельно ребру призмы) до пересечения с основной плоскостью (плоскостью основания). На изображении призмы показать, как находить основания данных точек. Затем перейти к выяснению нового способа построения сечений многогранников. Разъясним его с помощью рисунка

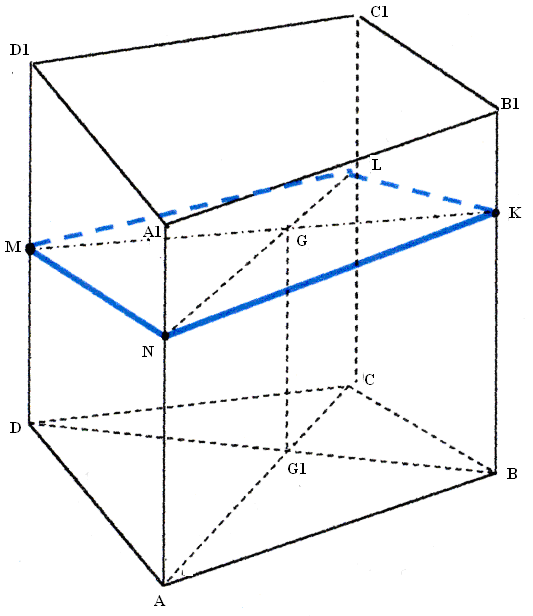
Для построения искомого сечения призмы ABCDA1B1C1D1 плоскостью, проходящей через точки M, N и K нужно построить точку L пересечения плоскости MNK с ребром СС1. Воспользуемся методом параллельного проектирования. Пусть L - искомая точка ребра СС1. Параллельной проекцией сечения MNKL на плоскость нижнего основания будет многоугольник DABC, проекцией отрезка является отрезок DB, а проекцией отрезка LM - отрезок CD. (Направление проектирования параллельно боковому ребру призмы). При указанном проектировании точка G пересечения отрезков МК и NL перейдет в точку G1 пересечения отрезков BD и АС. Отсюда вытекает следующее построение: проводим отрезки BD и АС, отмечаем точку G1 их пересечения, проводим через точку G1 прямую, параллельную боковому ребру призмы, и отмечаем точку G ее пересечения с отрезком МК. Точка пересечения ребра СС1 с прямой NG и является искомой точкой L. MNKL – искомое сечение. После решения задачи необходимо определять вид полученного сечения.

Далее нужно рассмотреть решение задач на построение сечений методом центрального проектирования. Чтобы не ошибиться в выборе необходимых для построения точек и прямых, учитель может предложить придерживаться определенного порядка: на основании пирамиды выбрать одну основную точку, и эту точку соединять с теми вершинами основания пирамиды, для которых нужно находить соответствующие точки на искомом сечении. Продолжить решение задач №1 и задач № 2, № 3, используя метод внутренних проекций.

Задача 2. Построить сечение пирамиды EABCD, плоскостью, проходящей через точки M, K, N.

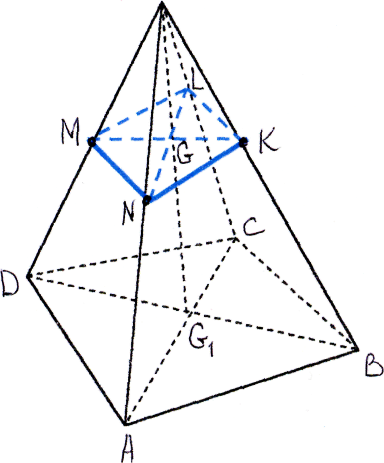
Решение.

Примем за центр проектирования точку Е. Тогда проекцией отрезка МК на плоскость основания пирамиды будет отрезок DB. Пусть G1 - точка пересечения отрезков DB и АС. Она является проекцией точки G (G = MK  EG1). Искомая точка L найдется как пересечение прямой NG с прямой EC. Четырехугольник MNKL - искомый.

Задача 3. Усечь пирамиду SA1B1C1D1E1 плоскостью АВС, проходящей через данные точки А, В, С на ребрах пирамиды.

( решение показано на рисунке )

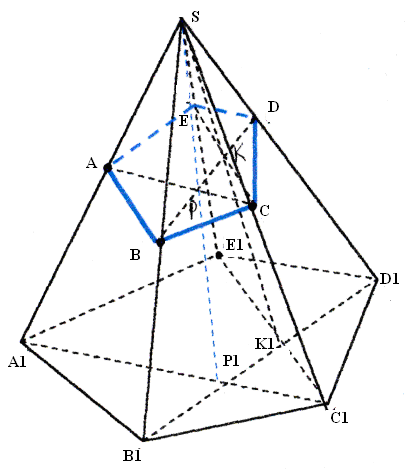
Несколько слов об оформлении задач на построение сечений.

При решении задач на построение лучше ограничиться описанием построения. В каждом пункте указывать, какая точка и прямая строится и как она строится. Дальше описать, какое отношение к некому сечению имеет полученная точка или прямая. Анализ сводится к выбору прямой, принадлежащей плоскости, и плоскости (пересечение которых надлежит построить). Он выполняется по ходу построения устно. Доказательства в рассматриваемых задачах сводятся к обоснованию, почему построенная точка принадлежит пересечению плоскости сечения с плоскостью грани (ребра) и являются однотипными.

Формирующий этап.

Цель данного этапа – систематизировать знания о методах построения сечений, сформировать умение выбора наиболее рационального метода.

После изучения методов построения сечений на формирующем этапе проводится обобщение, которое может быть представлено в виде таблицы.

Чтобы хорошо запомнить материал, можно заполнить таблицу.

Метод следов

Метод внутреннего проектирования

Главным здесь является то, что необходимо выбрать наиболее рациональный метод.

Далее можно решить несколько задач разными методами.

Задача.

Построить сечение фигуры через данные точки M, N, K.

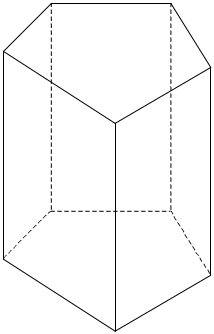
Совершенствующий этап.

На совершенствующем этапе продолжается развитие умений построения сечений и применения их при решении различных задач. В этих задачах построение сечений является не конечным результатом решения, а одним из этапов. Это могут быть задачи на нахождение:

1. площади сечения;

2. различных элементов многогранника по известной площади сечения;

3. боковой и полной поверхностей тел по известной площади сечения;

4. отношения площадей поверхности и сечения (Sполн / Sсеч);

5. объема тела, если известна площадь сечения и др.

Так, например, в главе "Объемы тел" мы можем найти задачи следующего содержания:

№ 24 ( Погорелов А.В.)

В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите объем призмы, если площадь сечения Q, а боковые ребра равны l.

№ 700 ( Атанасян Л.С.)

В правильной усеченной четырехугольной пирамиде стороны оснований равны 6 см и 4 см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15 см². найдите объем усеченной пирамиды.

При изучении темы "Построение сечений многогранников" на каждом этапе можно рассматривать решение некоторых устных задач из предложенных ниже.

Устные задачи по теме «Сечения многогранников».

1. Как может быть расположена плоскость относительно многогранника?

2. В каком случае говорят о сечении многогранника плоскостью?

3. Какой фигурой является сечение многогранника плоскостью?

4. В каком случае задача на построение сечения многогранника плоскостью считается решенной?

5. Как может быть задана плоскость сечения?

6. Как найти на чертеже пересечение двух пересекающихся прямых?

7. Как найти на чертеже пересечение прямой и плоскости? Что для этого должно быть задано?

8. Как найти на чертеже пересечение двух плоскостей? Что для этого должно быть задано?

9. Может ли в сечении куба (A…D1) плоскостью получиться: а) квадрат; б) прямоугольник; в) параллелограмм; г) ромб?

10. Может ли в сечении куба плоскостью получиться: а) пятиугольник; б) правильный пятиугольник?

11. Может ли в сечении куба плоскостью получиться: а) шестиугольник; б) правильный шестиугольник?

12. Может ли в сечении куба плоскостью получиться семиугольник? Многоугольник с числом сторон больше шести?

13. Какой многоугольник с наибольшим числом сторон может получиться в сечении: а) тетраэдра; б) четырёхугольной пирамиды; в) шестиугольной призмы; г) n-угольной призмы?

14. Какое сечение призмы называется диагональным?

15. Сколько диагональных сечений у а) треугольной; б) четырёхугольной; в) пятиугольной; г) n-угольной призмы?

16. Какой фигурой является сечение куба плоскостью, проходящей через концы трёх ребер, исходящих из одной вершины?

17. Возьмите одну из вершин верхнего основания куба. В нижнем основании возьмите проекцию этой вершины. В плоскости нижнего основания возьмите два ребра, исходящие из неё. Проведите плоскость через концы этих рёбер и первую вершину. Какой фигурой будет сечение? Найдите его периметр, если длина ребра куба равна 1.

18. Какой фигурой является сечение куба A…D1 плоскостью, проходящей через вершины В1, D и точку К - середину ребра СС1?

19. Какой фигурой является сечение куба A…D1 плоскостью, проходящей через точки E, F, G - середины соответственно ребер AD, A1B1, B1С1?

20. В какой правильной n-угольной призме все диагональные сечения равны между собой?

21. Определите вид сечения правильной треугольной призмы плоскостью, проходящей через сторону нижнего основания и середину скрещивающейся с ней стороны верхнего основания.

22. Верно ли утверждение о том , что в сечении правильной шестиугольной призмы плоскостью, проходящей через середины двух соседних боковых ребер и вершину верхнего основания, принадлежащей смежной боковой грани, получается равнобедренная трапеция?

23. Может ли прямоугольник быть одним из диагональных сечений наклонной призмы? Приведите пример такой призмы.

24. Найдите площадь сечения куба плоскостью, проходящей через три точки, взятые в серединах его рёбер, выходящих из одной вершины. Длина ребра куба равна 1.

25. Какой фигурой является сечение куба плоскостью, которая проходит через две противоположные вершины нижнего основания и середину одного из ребер верхнего основания? Найдите его периметр, если длина ребра куба равна 1.

26. Какой фигурой является сечение правильного тетраэдра AВСD плоскостью, проходящей через вершину В и точки М, N- середины соответственно сторон AD, СD?

27. Как построить сечение правильного тетраэдра AВСD плоскостью, параллельной грани ВDС и проходящей через точку К - середину ребра AD?

28. Как пересечь правильную треугольную призму тремя плоскостями таким образом, чтобы получилась правильная шестиугольная призма?

Вывод.

Из вышесказанного ясно, что обучение учащихся решению задач на построение сечений способствует развитию конструктивных навыков, более сознательному усвоению и применению теоретических знаний (особенно аксиом стереометрии и их следствий).

Я считаю, что материал, который предлагается в данной работе, будет достаточным для усвоения учащимися различных способов построения сечений многогранников.

Список используемой литературы.

1. Вавилов В. Сечение многогранников. / Квант. 1979. № 1.

2. Владимирский Г.А. О методах использования чертежа в преподавании геометрии./ Математика в школе, 1946, № 4.

3. Вопросы методики преподавания стереометрии / Под ред. Репьева В.В. – Горький: Горьковский госпединститут, 1961.

4. Глейзер Г.Д. Психолого-математические основы развития пространственных представлений при обучении геометрии. М., Просвещение, 1980.

5. Гриб Г.Р., Сергеев В.Н., Шурыгина О.В. Подготовленность выпускников девятого класса к продолжению математического образования. Омск, 1992.

6. Далингер В.А. Методика формирования пространственных представлений у учащихся при обучении геометрии. Омск: издательство Омского пединститута, 1992.

7. Зенгин А.Р. Основные принципы построения изображений в стереометрии. М., Учпедгиз, 1956.

8. Зинченко В.П., Вергилес Н.Ю. Формирование зрительного образа. Исследование деятельности зрительной системы. М., 1969.

9. Изаак Д.Ф. К методике решения задач на построение сечений призм и пирамид. / Математика в школе, 1978, № 5.

10. Изаак Д.Ф. Об изображении пространственных фигур. / Математика в школе, 1956, № 5.

11. Казаков П.Г. Параллельные проекции и методы решения конструктивных задач. Пособие для учителей. М., Учпедгиз, 1960.

12. Каплунович И.Я. Диагностика умений школьников оперировать пространственными образами и оперирования в пространстве./ Психодиагностика и школа: Тезисы докладов симпозиума. Таллин, 1980.

13. Лернер Г.И. Психология восприятия объемных форм. М., 1980.

14. Лурье И.А. Об упражнениях для формирования пространственных представлений./ Математика в школе, 1981, № 6.

15. Маслова Г.Г. Развитие пространственных представлений при решении задач./ Математика в школе, 1964, № 3.

16. Платонова В.И. к вопросу о развитии пространственных представлений учащихся. / Математика в школе, 1984, № 6.

17. Прасолов В.В., Шарыгин И.Ф. Задачи по стереометрии. М., Наука, 1989.

18. Семушин А.Д. Методика обучению решению задач на построение по стереометрии. М., Изд-во АПН РСФСР, 1959.

19. Четверухин Н.Ф. Изображение фигур в курсе геометрии. М., Учпедгиз, 1958.

20. Четверухин Н.Ф. Геометрические характеристики причины трудности узнавания фигур на чертеже./ Математика в школе, 1965, № 4.

21. Четверухин Н.Ф. Стереометрические задачи на проекционном чертеже. М., Учпедгиз, 1955.

22. Якиманская И.С. Основные направления исследования образного мышления. / Вопросы психологии, 1985, № 5.

Оглавление

Введение. Актуальность темы.	1-5
Глава I.	5-11
Тест № 1. Пространственное мышление (стандартное восприятие).	5
Тест №2. Пространственное мышление (продвинутый уровень).	3
Роль чертежа в развитии пространственных представлений.	4-7
Методы изображения многогранников.	7
Метод параллельного проектирования.	7-9
Центральное проектирование.	9-10
Роль задач на построение сечений в школьном курсе стереометрии.	10-11
Глава II.	13-20
8. Обучение решению задач на построение сечений многогранников	11-
а) Подготовительный этап.	11-13
б) Ознакомительный этап.	13-16
9. Введение метода внутреннего проектирования.	16-18
в) Формирующий этап.	18
г) Совершенствующий этап.	19
10. Устные задачи по теме «Сечения многогранников»	19-20
11. Вывод.	20
12. Список использованной литературы.	21
13. Оглавление	22

7