Методы построения сечений многогранников

Методы построения сечений многогранников

Иванова Саргылаана Семеновна

В школе плоские сечения многогранников строят лишь на основании аксиом и теорем стереометрии. Вместе с тем существуют и другие методы построения плоских сечений многогранников. Наиболее эффективными являются метод следов, метод внутреннего проектирования и комбинированный метод. Очень интересен и перспективен в плане применения к решению различных задач координатный метод. Если многогранник поместить в систему координат, а секущую плоскость задать уравнением, то построение сечения сведется к отысканию координат точек пересечения плоскости с ребрами многогранника.

Целью исследования является изучение различных методов построения сечений многогранников. Для этого изучен теоретический материал по данной теме, систематизированы методы решения задач на построение сечений, приведены примеры задач на применение каждого метода, рассмотрены примеры задач единого государственного экзамена на построение сечений и вычисление их элементов.

• Объект исследования : методы построения сечений многогранников.
• Цель исследования : изучить различные методы построения сечений многогранников.
• Задачи исследования :

1) Изучить теоретический материал по данной теме.

2) Систематизировать методы решения задач на построение сечений.

3) Привести примеры задач на применение каждого метода.

4) Рассмотреть примеры задач единого государственного экзамена на построение сечений и вычисление их элементов.

РАЗДЕЛ 1 ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ НА ОСНОВЕ СИСТЕМЫ АКСИОМ СТЕРЕОМЕТРИИ

Определение . Сечением многогранника плоскостью называется геометрическая фигура, представляющая собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости; плоскость при этом называется секущей плоскостью.

Поверхность многогранника состоит из ребер - отрезков и граней - плоских многоугольников. Так как прямая и плоскость пересекаются в точ­ке, а две плоскости - по прямой, то сечением многогранника плоскостью является плоский многоугольник; вершинами этого многоугольни­ка служат точки пересечения секущей плоскости с ребрами многогранника, а сторонами - отрез­ки, по которым секущая плоскость пересекает его грани. Это означает, что для построения искомо­го сечения данного многогранника плоскостью α   достаточно построить точки ее пересечения с реб­рами многогранника. Затем последовательно со­единить отрезками эти точки.

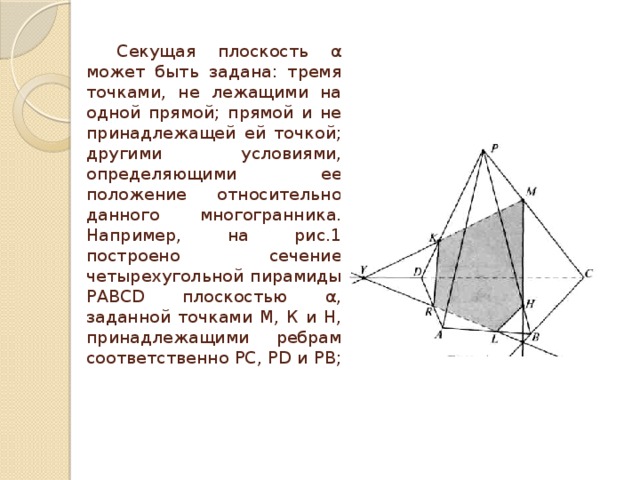
Секущая плоскость α может быть задана: тремя точками, не лежащими на одной прямой; пря­мой и не принадлежащей ей точкой; другими ус­ловиями, определяющими ее положение относи­тельно данного многогранника. Например, на рис.1 построено сечение четырехугольной пирамиды РАВСD плоскостью α, заданной точками М, К и Н, принадлежащими ребрам соответственно РС, РD и РВ;

Задача. В параллелепипеде АВСDA 1 B 1 C 1 D 1 постройте сечение плоскостью, проходящей через вершины C и D 1 и точку K отрезка B 1 C 1 (рис.2, а).

а)

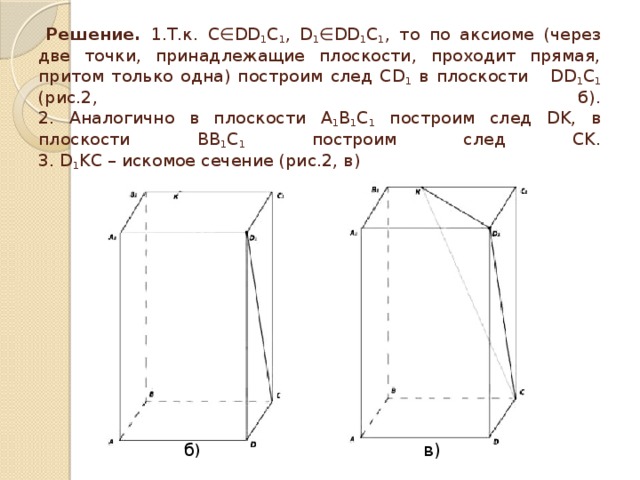
Решение. 1.Т.к. С∈DD 1 C 1 , D 1 ∈DD 1 C 1 , то по аксиоме (через две точки, принадлежащие плоскости, проходит прямая, притом только одна) построим след CD 1 в плоскости DD 1 C 1 (рис.2, б). 2. Аналогично в плоскости А 1 В 1 С 1 построим след DK, в плоскости BB 1 C 1 построим след CK. 3. D 1 KC – искомое сечение (рис.2, в)

б )

в)

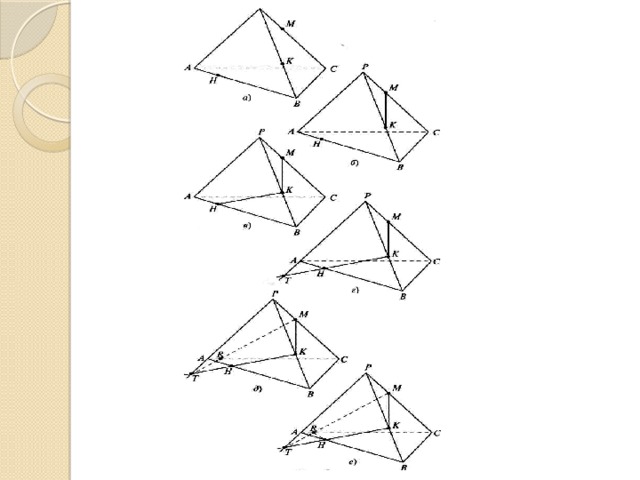
Задача.  Постройте сечение пирамиды РАВС плоскостью α = (МКH), где М, К и Н — внутренние точки соответственно ребер РС, РВ и АВ (рис. 3, а).

Решение.  1-й шаг. Точки М и K лежат в каждой из двух плоскостей α и РВС. Поэтому по аксиоме пересечения двух плоскостей плос­кость α пересекает плоскость РВС по прямой МК. Следовательно, отрезок МК — одна из сто­рон искомого сечения (рис.3, б).

2-й шаг. Аналогично, отрезок КН — другая сто­рона искомого сечения (рис.3, в).

3-й шаг. Точки М и Н не лежат одновремен­но ни в одной из граней пирамиды РАВС, поэто­му отрезок МН не является стороной сечения этой пирамиды. Прямые КН и РА лежат в плос­кости грани АВР и пересекаются. Построим точ­ку T= КН ∩АР (рис. 3, г).

Поскольку прямая КН лежит в плоскости α, то и точка T лежит в плоскости α. Теперь мы видим, что плоскости α   и АРС имеют общие точки М и T. Следовательно, по аксиоме пе­ресечения двух плоскостей плоскость α и плос­кость АРС пересекаются по прямой МТ, кото­рая, в свою очередь, пересекает ребро АС в точке R (рис. 3, д).

4-й шаг. Теперь так же, как в шаге 1, устанав­ливаем, что плоскость α пересекает грани АСР и АВС по отрезкам MR и HR соответственно. Следовательно, искомое сечение — четырехуголь­ник MKHR (рис.3,е).

РАЗДЕЛ 2 МЕТОД СЛЕДОВ В ПОСТРОЕНИИ СЕЧЕНИЙ МНОГОГРАННИКОВ

Определение . Прямая, по которой секущая плоскость α пересекает плоскость основания многогранника, называется следом плоскости α в плоскости этого основания.

Из определения следа получаем: в каж­дой его точке пересекаются прямые, одна из которых лежит в секущей плоскости, другая - в плоскости основания. Имен­но это свойство следа используют при по­строении плоских сечений многогранников методом следов. При этом в секущей плоскости удобно использовать такие прямые, ко­торые пересекают ребра многогранника.

Сначала секущую плоскость зададим ее следом в плоскости основания призмы (пирамиды) и точкой, принадлежащей по­верхности призмы (пирамиды).

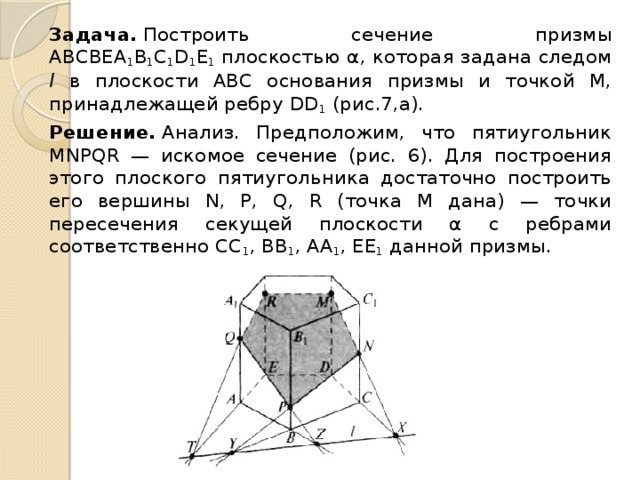
Задача.  Построить сечение призмы АВСВЕА 1 В 1 С 1 D 1 Е 1  плоскостью α, которая задана следом l в плоскости АВС основа­ния призмы и точкой М, принадлежащей ребру DD 1 (рис.7,а).

Решение.  Анализ. Предположим, что пятиугольник MNPQR — искомое сечение (рис. 6). Для построения этого плоского пятиугольника достаточно построить его вершины N, P, Q, R (точка М дана) — точки пересечения секущей плоскости α с ребрами соответственно СС 1 , ВB 1 , АА 1 , ЕЕ 1  данной призмы.

Для построения точки N = α ∩ СС 1  до­статочно построить прямую пересечения секущей плоскости α с плоскостью грани СDD 1 C 1 . Для этого, в свою очередь, доста­точно построить в плоскости этой грани еще одну точку, принадлежащую секущей плоскости α. Как построить такую точку?

Так как прямая l лежит в плоскости осно­вания призмы, то она может пересекать пло­скость грани СDD 1 C 1  лишь в точке, которая принадлежит прямой CD = (CDD 1 ) ∩ (АВС), т.е. точка X = l ∩ СD = l ∩ (CDD 1 ) принад­лежит секущей плоскости α. Таким образом, для построения точки N = α ∩ СС 1  достаточно построить точку X = l ∩ СD. Аналогично, для построения точек Р = α ∩ ВВ 1 , Q = α ∩ АА 1  и R = α ∩ ЕЕ 1  достаточно построить соответственно точ­ки: У = l ∩ ВС, Z = l ∩ АВ и Т = l ∩ АЕ. Отсюда

Построение. 

1. X = l ∩ СD (рис. 7, б);

2. N = МХ ∩ СС 1  (рис. 7, б);

3. У = l ∩ ВС (рис. 7, в);

4. Р = NY ∩ ВВ 1  (рис. 7, в);

5. Z = l ∩ АВ (рис. 7, в);

6. Q= РZ ∩ АА 1  (рис. 7, г);

7. T= l ∩ АЕ (рис. 6);

8. R= QT ∩ ЕЕ 1  (рис. 6).

Пятиугольник MNPQR — искомое сече­ние (рис. 6).

МХ є α, тогда МХ ∩ СС 1  = N є α , значит, N = α ∩ СС 1 ; N є α, Y є α = NY є α, тогда NY ∩ ВВ 1 = Р є α, значит, Р = α ∩ ВВ 1 ; Р є α, Z є α = РZ є α, тогда PZ ∩ AА 1  = Q є α, значит, Q = α ∩ АA 1 ; Q є α, T є α = QТ є α, тогда QТ ∩ EЕ 1  =R є α, значит, R = α ∩ ЕЕ 1 . Следовательно, MNPQR - искомое се­чение. " width="640"

Доказательство . Так как прямая l - след секущей плоскости α, то точки X = l ∩ СD, Y = l ∩ ВС, Z = l ∩ АВ и T= l ∩ АЕ принадлежат этой плоскости.

Поэтому имеем:

М є α , X є α = МХ є α, тогда МХ ∩ СС 1  = N є α , значит, N = α ∩ СС 1 ;

N є α, Y є α = NY є α, тогда NY ∩ ВВ 1 = Р є α, значит, Р = α ∩ ВВ 1 ;

Р є α, Z є α = РZ є α, тогда PZ ∩ AА 1  = Q є α, значит, Q = α ∩ АA 1 ;

Q є α, T є α = QТ є α, тогда QТ ∩ EЕ 1  =R є α, значит, R = α ∩ ЕЕ 1 .

Следовательно, MNPQR - искомое се­чение.

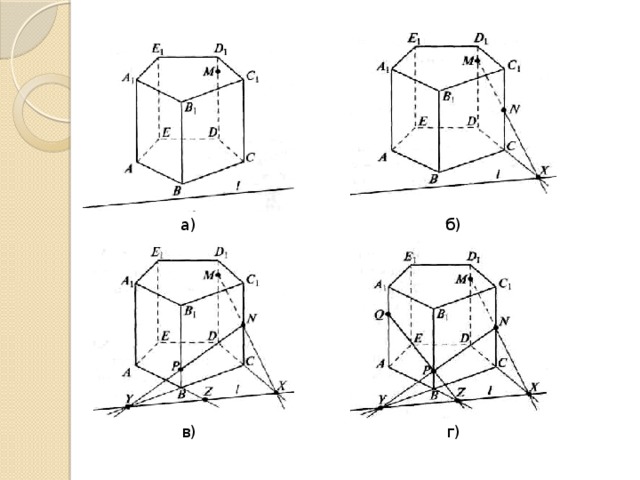
а)

б)

в)

г)

Исследование . След l секущей плоско­сти α не пересекает основание призмы, а точка М секущей плоскости принадле­жит боковому ребру DD 1  призмы. Поэто­му секущая плоскость α не параллельна боковым ребрам. Следовательно, точки N, Р, Q и R пересечения этой плоскости с боковыми ребрами призмы (или продолжениями этих ребер) всегда существуют. А поскольку, кроме того, точка М не при­надлежит следу l , то определяемая ими плоскость α единственна. Это означает, что задача имеет единственное ре­шение.

Задача.  Построить сечение пятиуголь­ной пирамиды PABCDE плоскостью, ко­торая задана следом l и внутренней точ­кой К ребра РЕ.

Решение.  Схематически построение искомого сечения можно изобразить так (рис.8): T 1  → Q → Т 2  → R → Т 3  → М → Т 4  → N.

Пятиугольник MNKQR — искомое се­чение.

«Цепочка» последовательности построе­ния вершин сечения такова:

1. Т 1 = l ∩ АЕ; 2. Q = Т 1 К ∩ РА;

3. Т 2  = l ∩ АВ; 4. R = Т 2 Q ∩ РВ;

5. Т 3  = l ∩ ВС; 6. М = T 3 R ∩ РС;

7. Т 4  = l ∩ СD; 8. N = Т 4 М ∩ РD.

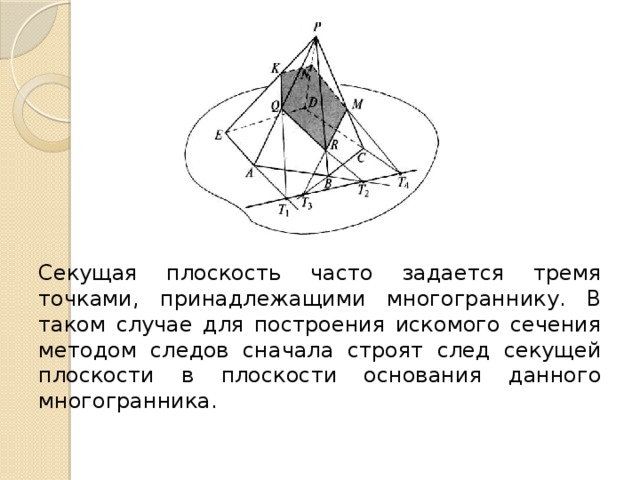
Секущая плоскость часто за­дается тремя точками, принадлежащими многограннику. В таком случае для построения искомо­го сечения методом следов сначала строят след секущей плоскости в плоскости осно­вания данного многогранника.

РАЗДЕЛ 3 МЕТОД ВНУТРЕННЕГО ПРОЕКТИРОВАНИЯ В ПОСТРОЕНИИ СЕЧЕНИЙ МНОГОГРАННИКОВ

Метод внутреннего проекти­рования называют еще методом соответствий, или методом диагональных сечений.

При применении этого метода каждая заданная точка проектируется на плоскость основания. Существует два возможных вида проектирования: центральное и параллельное. Центральное проектирование, как правило, используется при построении сечений пирамид, вершина пирамиды при этом является центром проекции. Параллельное проектирование используется при построении сечений призм.

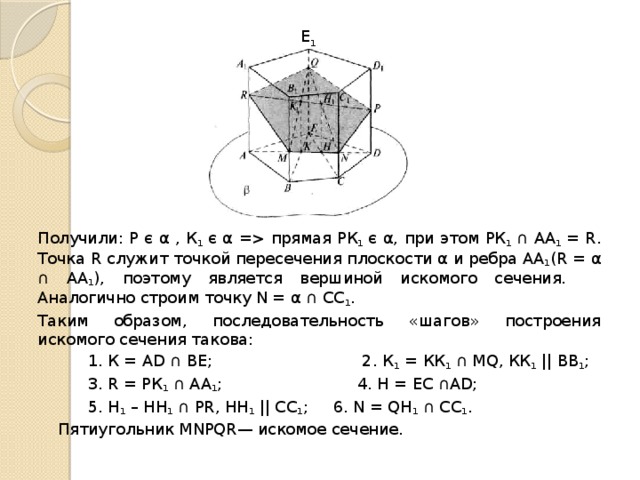
Задача . Постройте сечение призмы АВСDEА 1 В 1 С 1 D 1 Е 1 , плоскостью α, задан­ной точками М є ВВ 1 , Р є DD 1 , Q є ЕЕ 1  (рис.10).

Решение. Обозначим: β — плоскость нижнего основания призмы. Для построения искомого сечения построим точки пересече­ния плоскости α = (МРQ) с ребрами призмы.

Построим точку пересечения плоскости α с ребром АА 1 .

Плоскости А 1 АD и ВЕЕ 1  пересекают плоскость β по прямым соответственно АD и ВЕ, которые пересекаются в неко­торой точке К. Так как плоскости А 1 АD и ВЕЕ 1  проходят через параллельные ре­бра АА 1  и ВВ 1  призмы и имеют общую точку К, то прямая КК 1  их пересечения проходит через точку К и параллельна ре­бру ВВ 1 . Точку пересечения этой прямой с прямой QМ обозначим: К 1 = КК 1  ∩ QМ, КК 1  ║ ВВ 1 . Так как QM є α, то К 1  є α.

прямая РК 1  є α, при этом РК 1  ∩ АА 1  = R. Точка R служит точкой пересечения плоскости α и ребра АА 1 (R = α ∩ АА 1 ), поэтому является вершиной искомого сечения. Аналогично строим точку N = α ∩ СС 1 . Таким образом, последовательность «шагов» построения искомого сечения та­кова: 1. К = АD ∩ ВЕ; 2. К 1  = КК 1  ∩ MQ, КК 1  || ВВ 1 ; 3. R = РК 1  ∩ АА 1 ; 4. Н = ЕС ∩АD; 5. H 1  – HH 1  ∩ РR, НН 1  || СС 1 ; 6. N = QН 1  ∩ СС 1 . Пятиугольник MNPQR— искомое сечение. " width="640"

Е 1

Получили: Р є α , К 1  є α = прямая РК 1  є α, при этом РК 1  ∩ АА 1  = R. Точка R служит точкой пересечения плоскости α и ребра АА 1 (R = α ∩ АА 1 ), поэтому является вершиной искомого сечения. Аналогично строим точку N = α ∩ СС 1 .

Таким образом, последовательность «шагов» построения искомого сечения та­кова:

1. К = АD ∩ ВЕ; 2. К 1  = КК 1  ∩ MQ, КК 1  || ВВ 1 ;

3. R = РК 1  ∩ АА 1 ; 4. Н = ЕС ∩АD;

5. H 1  – HH 1  ∩ РR, НН 1  || СС 1 ; 6. N = QН 1  ∩ СС 1 .

Пятиугольник MNPQR— искомое сечение.

РАЗДЕЛ 4 КОМБИНИРОВАННЫЙ МЕТОД ПОСТРОЕНИЯ СЕЧЕНИЙ МНОГОГРАННИКОВ

Сущность комбинированного метода по­строения сечений многогранников состоит в следующем. На некоторых этапах по­строения сечения применяется или метод следов, или метод внутреннего проекти­рования, а на других этапах построения этого же сечения используются изученные теоремы о параллельности, перпендику­лярности прямых и плоскостей.

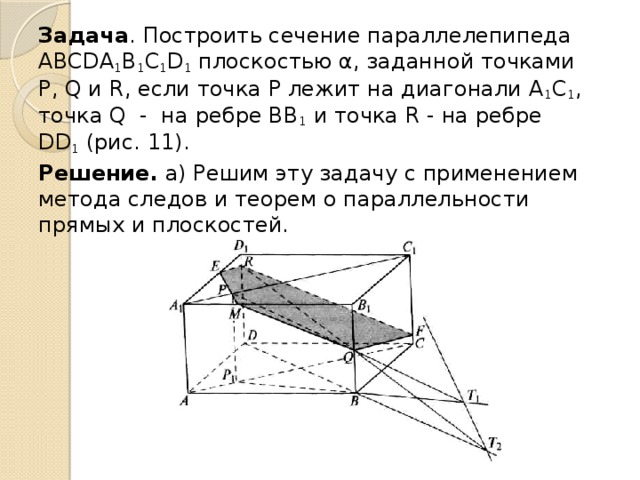
Задача . Построить сечение паралле­лепипеда АВСDА 1 В 1 С 1 D 1  плоскостью α, заданной точками Р, Q и R, если точка Р лежит на диагонали А 1 C 1 , точка Q - на ребре ВВ 1  и точка R - на ребре DD 1  (рис. 11).

Решение. а) Решим эту задачу с при­менением метода следов и теорем о парал­лельности прямых и плоскостей.

Построим след секущей плоскости α = (РQR) на плоскости АВС Для этого строим точки Т 1  = РQ ∩ Р 1 В, где PP 1 ║AA 1 , P 1 є AC, и T 2  = RQ ∩ ВD. По­строив след Т 1 Т 2 , замечаем, что точка Р лежит в плоскости А 1 B 1 C 1 , которая парал­лельна плоскости АВС. Это означает, что плоскость α пересекает плоскость А 1 B 1 C 1  по прямой, проходящей через точку Р и параллельной прямой Т 1 Т 2 . Проведем эту прямую и обозначим через М и Е точки ее пересечения с ребрами соответственно А 1 B 1  и А 1 D 1 . Получаем: М = α ∩ А 1 B 1 , Е =α∩ А 1 D 1 . Тогда отрезки ЕR и QМ являются сторонами искомого сечения.

Далее, так как плоскость ВСС 1  парал­лельна плоскости грани ADD 1 A 1 , то пло­скость α пересекает грань ВСC 1 B 1  по от резку QF (F= α ∩ СС 1 ), параллельному прямой ЕR. Таким образом, пятиуголь­ник ERFQM - искомое сечение. Точку F можно получить, проведя RF║ MQ.

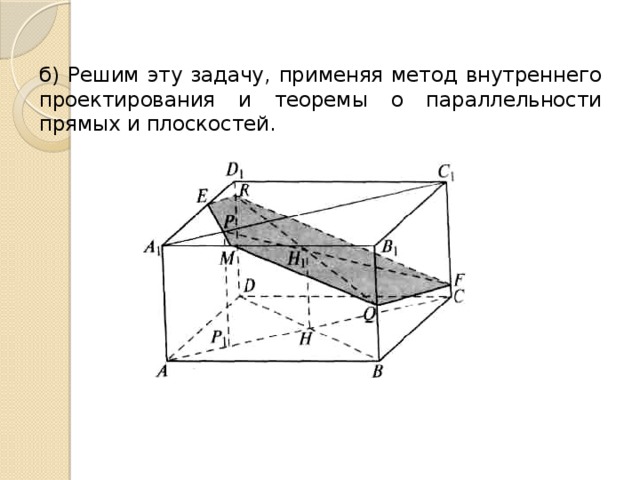
б) Решим эту задачу, применяя метод внутреннего проектирования и теоремы о параллельности прямых и плоскостей.

Пусть Н=АС ∩ ВD (рис. 12). Прове­дя прямую НН 1  параллельно ребру ВВ 1  (Н 1  є RQ), построим точку F: F=РН 1  ∩ CC 1 .Tочка F является точкой пересечения пло­скости α с ребром СС 1 , так как РН 1  є α. Тогда отрезки RF и QF, по которым пло­скость α пересекает соответственно грани CС 1 D 1 D и ВСС 1 В 1  данного параллелепипеда, являются сторонами его искомого сечения.

Так как плоскость АВВ 1  параллельна плоскости CDD 1 , то пересечением плоско­сти α и грани АВВ 1 А 1  является отрезок QМ (М є А 1 В 1 ), параллельный отрезку FR; отрезок QМ - сторона сечения. Далее, точка Е = МР ∩ А 1 D 1  является точкой пересечения плоскости α и ребра А 1 D 1 , так как МР є α. Поэтому точка Е - еще одна вершина искомого сечения. Таким образом, пятиугольник ERFQM - искомое сечение. Точку Е можно по­строить, проведя прямую RЕ ║ FQ. Тогда М = РЕ ∩ А 1 B 1 .

ЗАКЛЮЧЕНИЕ

В школе плоские сечения многогранников строят лишь на основании аксиом и теорем стереометрии. Вместе с тем существуют и другие методы построения плоских сечений многогранников. Наиболее эффективными являются метод следов, комбинированный метод. Очень интересен и перспективен в плане применения к решению различных задач координатный метод. Если многогранник поместить в систему координат, а секущую плоскость задать уравнением, то построение сечения сведется к отысканию координат точек пересечения плоскости с ребрами многогранника.

Целью исследования было изучение различных методов построения сечений многогранников. Для этого изучен теоретический материал по данной теме, систематизированы методы решения задач на построение сечений, приведены примеры задач на применение каждого метода, рассмотрены примеры задач единого государственного экзамена на построение сечений и вычисление их элементов.

Спасибо за внимание!