Муниципальное казенное общеобразовательное учреждение «Гимназия Табасаранского района»
Методическая разработка мастер –класса по физике
" Методы решения сложных цепей"
В рамках заседания МО учителей физики МР Табасаранский район»
Провела: учитель физики Ханахмедова Тамам Гамзатовна
Хучни 2024
Мастер-класс на тему:
Методы решения сложных цепей
Здравствуйте, уважаемые коллеги! Я Ханахмедова Тамам Гамзатовна, учитель физики МКОУ «Гимназия Табасаранского района». Хочу поделиться с вами опытом подготовки учащихся по теме «Электрические цепи»
Любую цепь можно рассчитать, используя уравнение Кирхгофа, однако они не входят в школьную программу. И кроме того, решать систему из большого числа уравнений со многими неизвестными- не лучший способ тратить время на олимпиаде или экзамене. Поэтому нужно уметь пользоваться методами, позволяющими быстро найти сопротивление цепи.
Я хочу на этом мастер классе рассказать о методах симметрии и эквипотенциальных узлов, а также о методе «Иоана Тихого», с помощью которого решаются бесконечные цепи.
Конечно о решении электрических цепей можно говорить много, но на мой взгляд, рассматриваемые методы самые доступные для учащихся 9-11 классов.
Метод симметрии.
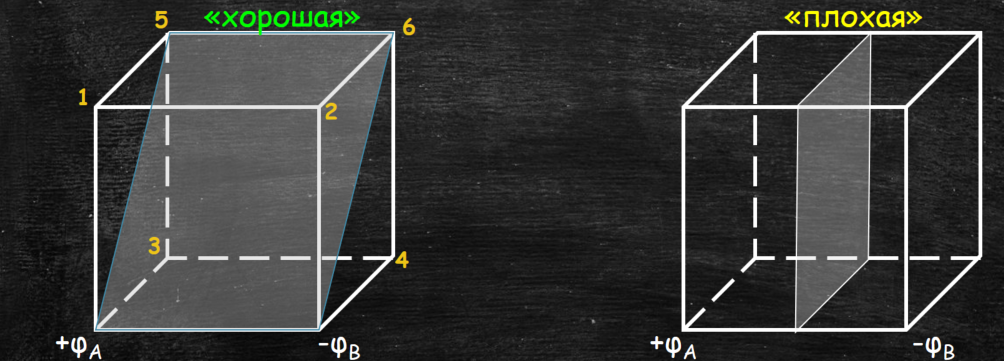
«Хорошая симметрия»
Прямая (плоскость сечения), проходящая через рассматриваемые точки. Относительно прямой соответствующие (симметричные) резисторы должны быть равны. При хорошей симметрии направление токов зеркально относительно симметрии, а токи равны.
«Плохая симметрия. Прямая (плоскость сечения), перпендикулярная линии, соединяющей рассматриваемые точки. Относительно прямой соответствующие (симметричные)резисторы должны быть равны. При «плохой» симметрии направление токов антизеркальны относительно симметрии, а токи равны.
Подробно метод симметрии рассмотрим на примерах решения задач.
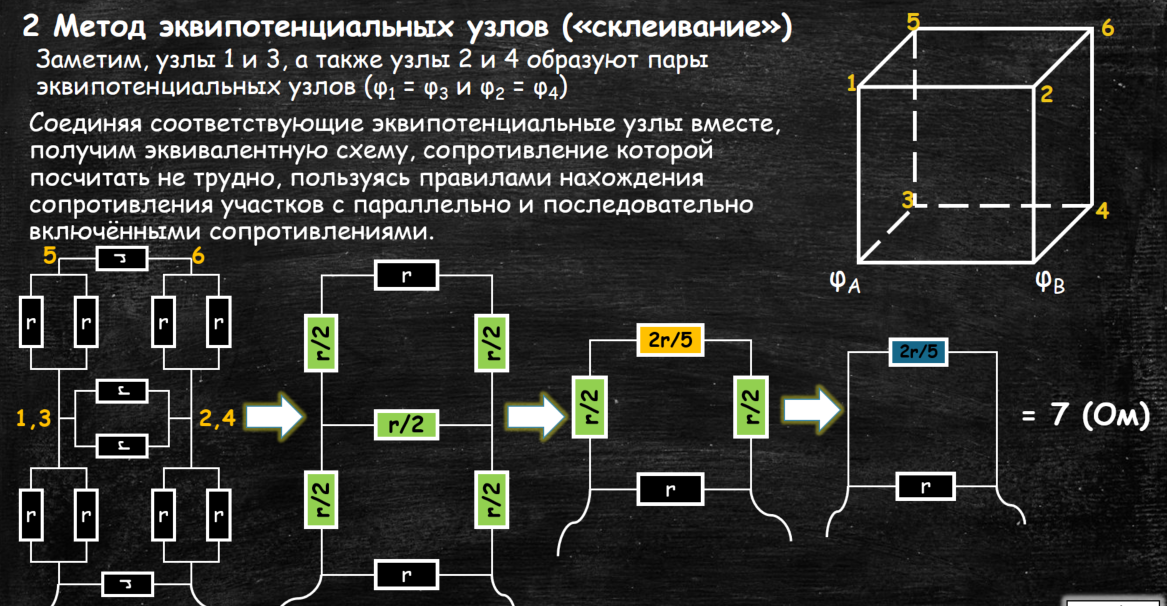
Метод эквипотенциальных узлов
Идея метода состоит в том, чтобы различные узла цепи, имеющие равные потенциалы, рассматривать как один узел. При этом потенциал в полученном «склеенном узле» равен значению потенциалов исходных узлов.
Как же найти эквипотенциальные узлы? Во многих случаях этому помогает «симметрия» включения участков цепи.
Так же сюда можно отнести метод исключения участка цепи – участок цепи, включенный между эквипотенциальным узлами, можно исключить из цепи; и метод «размножения узлов – обратный метод «склеивания» узлов.
Метод Иоана Тихого
Речь идёт о не простой ситуации: нужно поселить еще одного человека в гостиницу, все номера которой заняты. Особенность задачи состоит в том, что в гостинице бесконечное число номеров. Иоан решает эту задачу так: каждому обитателю гостиницы даётся приказ - перейти в комнату с номером, на единицу большим, чем номер его комнаты. При этом все прежние обитатели обеспечены жильём (ведь последнего - то номера нет в бесконечном ряду), а комната Nº1 освобождается для нового гостя.
Именно этот способ мы будем применять при решении бесконечной цепи.
Немного теоретического материала.
1) Реальный проводник (резистор). =R - сопротивление. Ток направлен от большего потенциала к - меньшему
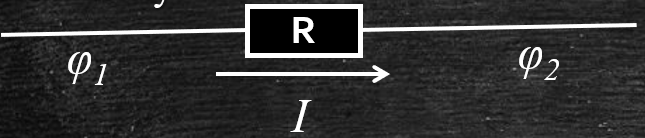
Мы можем один из потенциалов выбрать нулевым, например Ф2 = 0, тогда Ф1=Ф2=Ф1= IR=UR
Если Ф1=0, то Ф2= -IR
2) Идеальный проводник R = 0(ток течёт по инерции, создан или до или после участка)
Ф1 = Ф2 =Ф= 0 = I*0 = 0


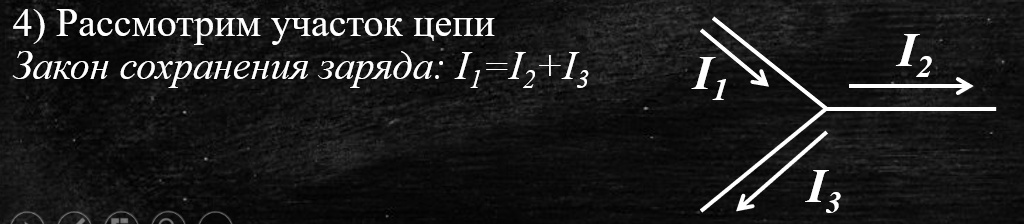
Проволочная сетка. Задача Nº1 (автор М. А. Пенкин) «хорошая» симметрия
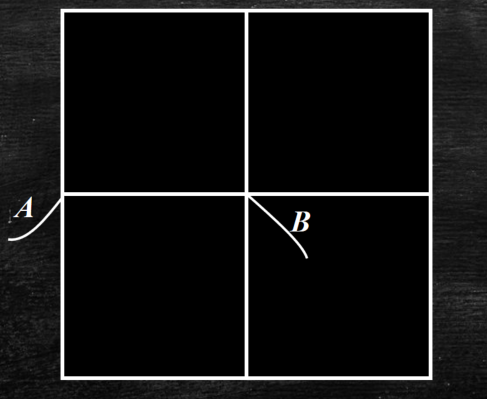
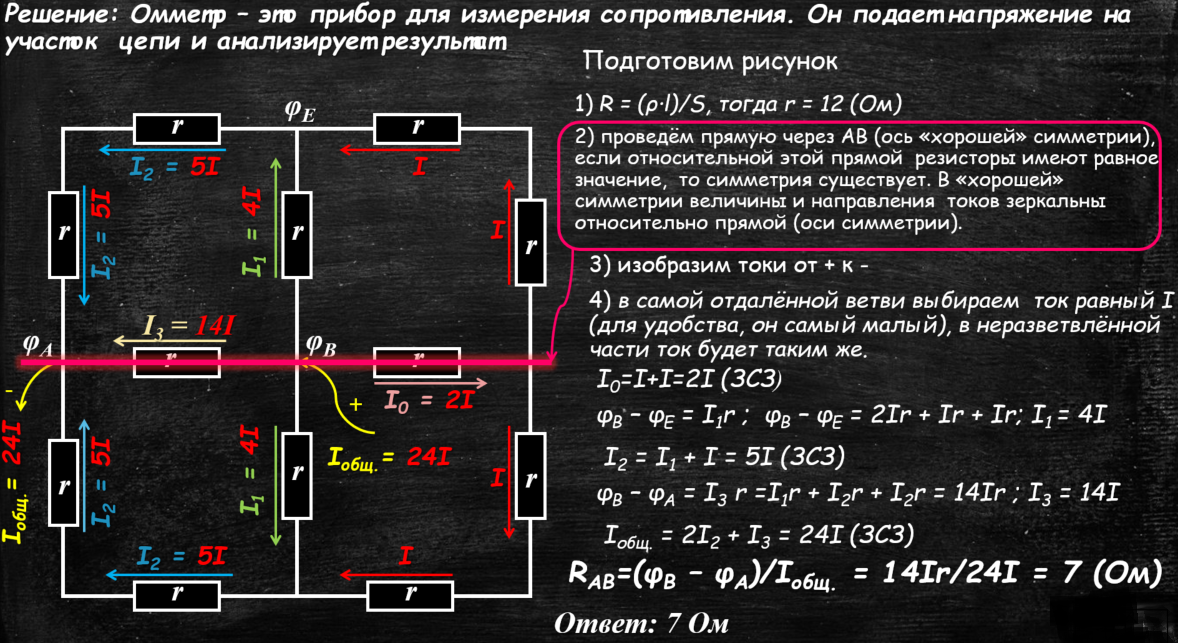
Кусок однородной проволоки. сопротивлением R=144 Ом разрезали на 12 равных по длине частей, из которых с помощью паяльника изготовили проволочную сетку. К двум указанным на рисунке спаям А и В подсоединили омметр. Какое сопротивление покажет прибор? Считать, что проволока имеет постоянное поперечное сечение.
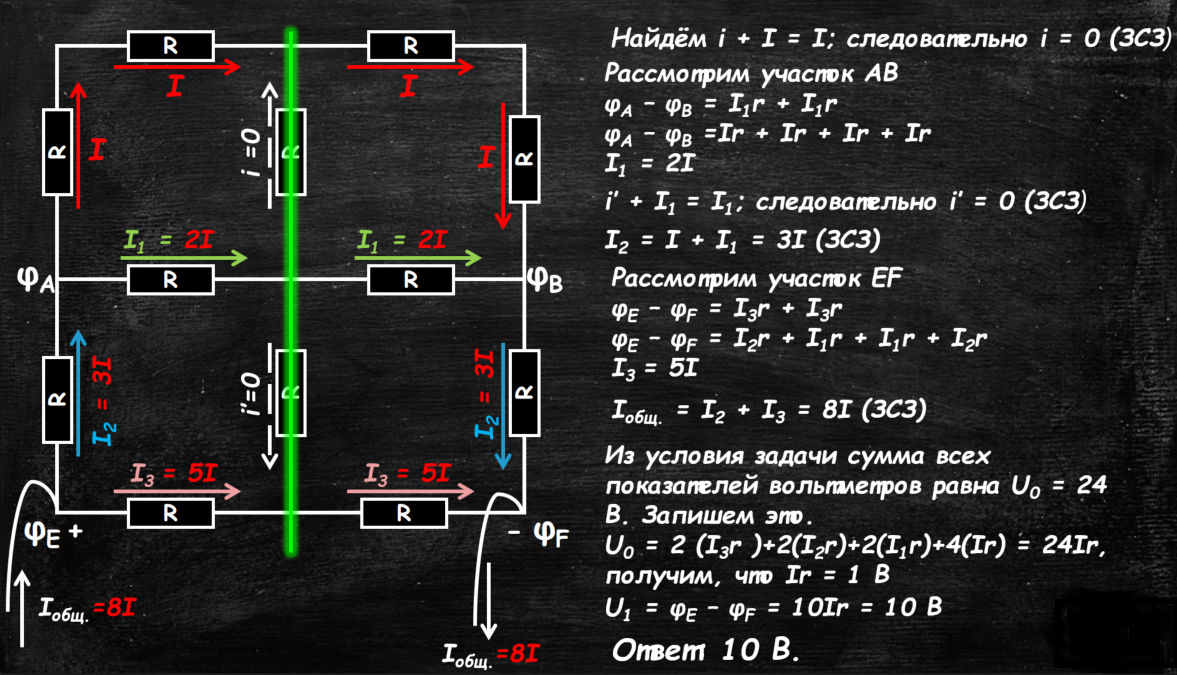
Сетка вольтметров. Задача Nº2 (автор М. А. Пенкин) «плохая» симметрия
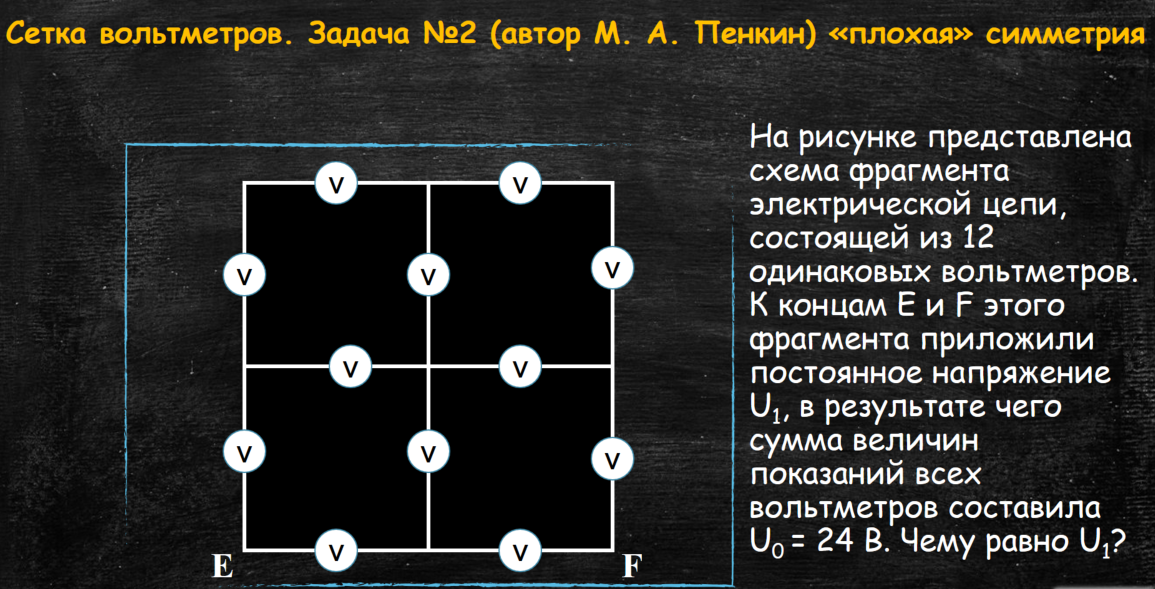
На рисунке представлена схема фрагмента электрической цепи, состоящей из 12 одинаковых вольтметров.
К концам Е и F этого фрагмента приложили постоянное напряжение
U1? в результате чего сумма величин показаний всех вольтметров составила F.
Uo = 24 В. Чему равно U1?
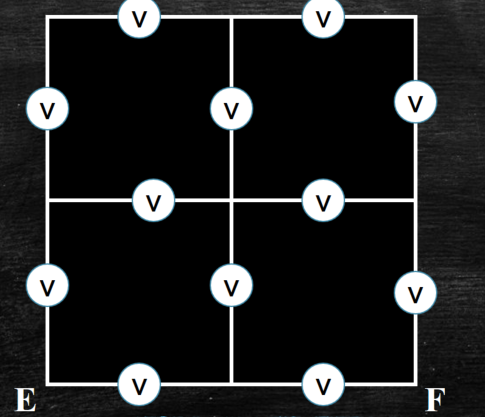
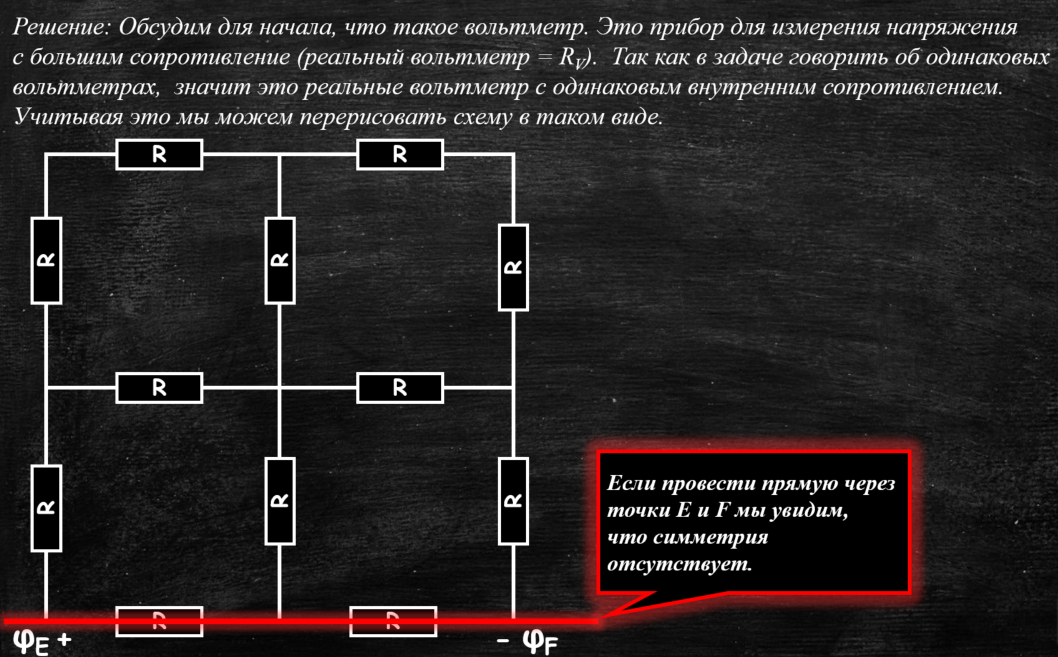
Решение: Обсудим для начала, что такое вольтметр. Это прибор для измерения напряжения с большим сопротивление (реальный вольтметр = Rv). Так как в задаче говориться об одинаковых вольтметрах, значит это реальные вольтметры с одинаковым внутренним сопротивлением.
Учитывая это мы можем перерисовать схему в таком виде.
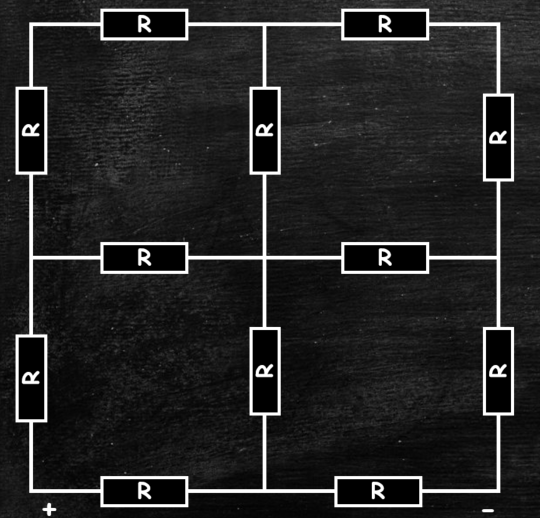
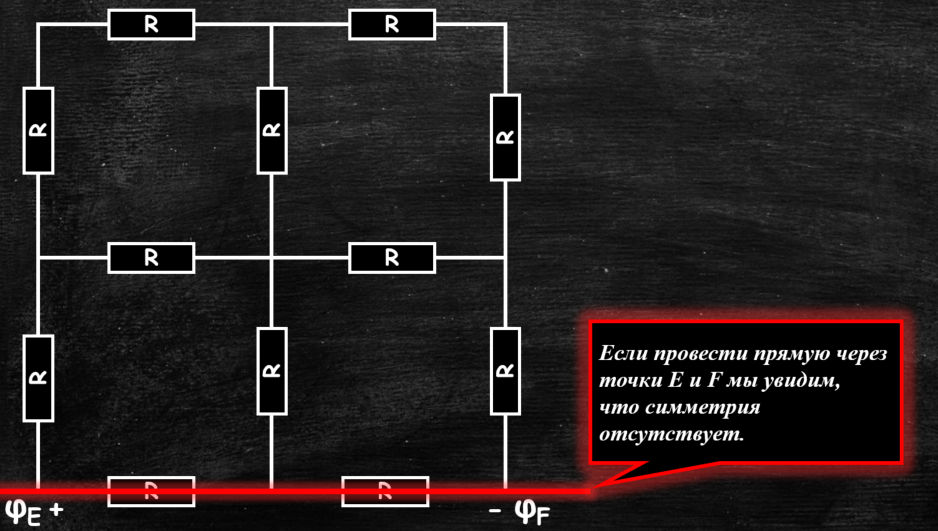
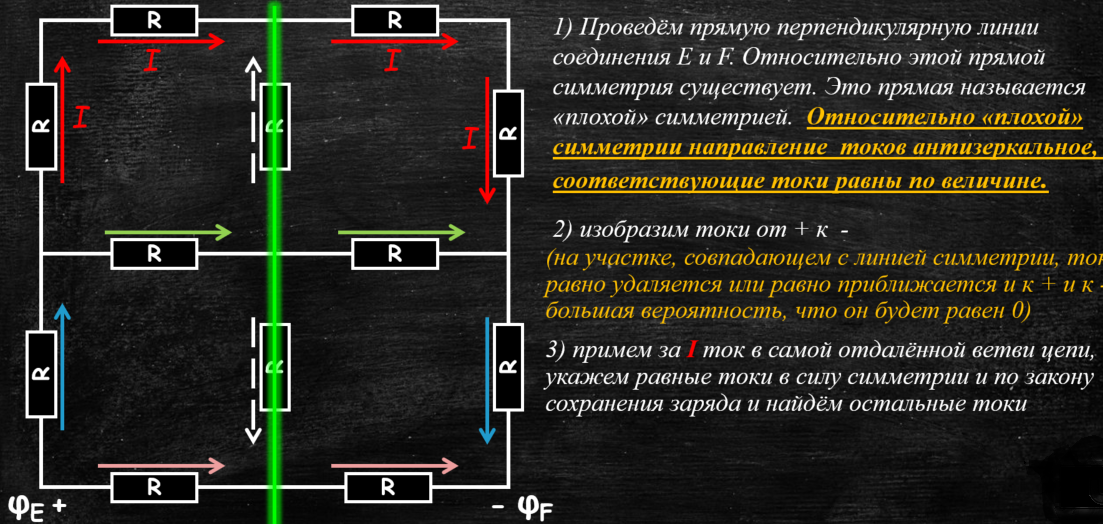
1) Проведем прямую, перпендикулярную линии соединения Е и F. Относительно этой прямой симметрия существует. Это прямая называется «плохой» симметрией. Относительно «плохой» симметрии направление токов антизеркальное, а соответствующие токи равны по величине.
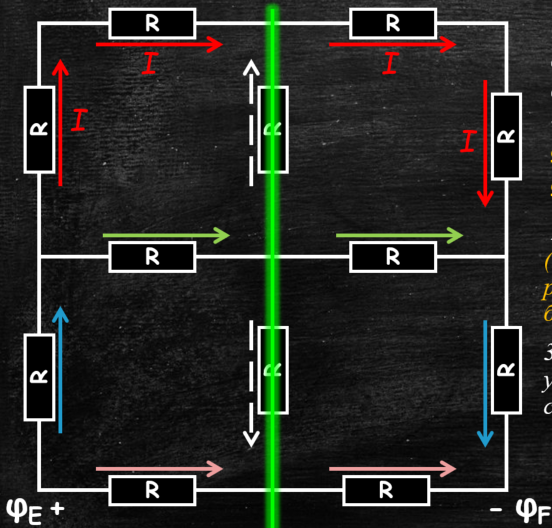
2) изобразим токи от + к -
(на участке, совпадающем с линией симметрии, ток равно удаляется или равно приближается и к + и к -; большая вероятность, что он будет равен 0)
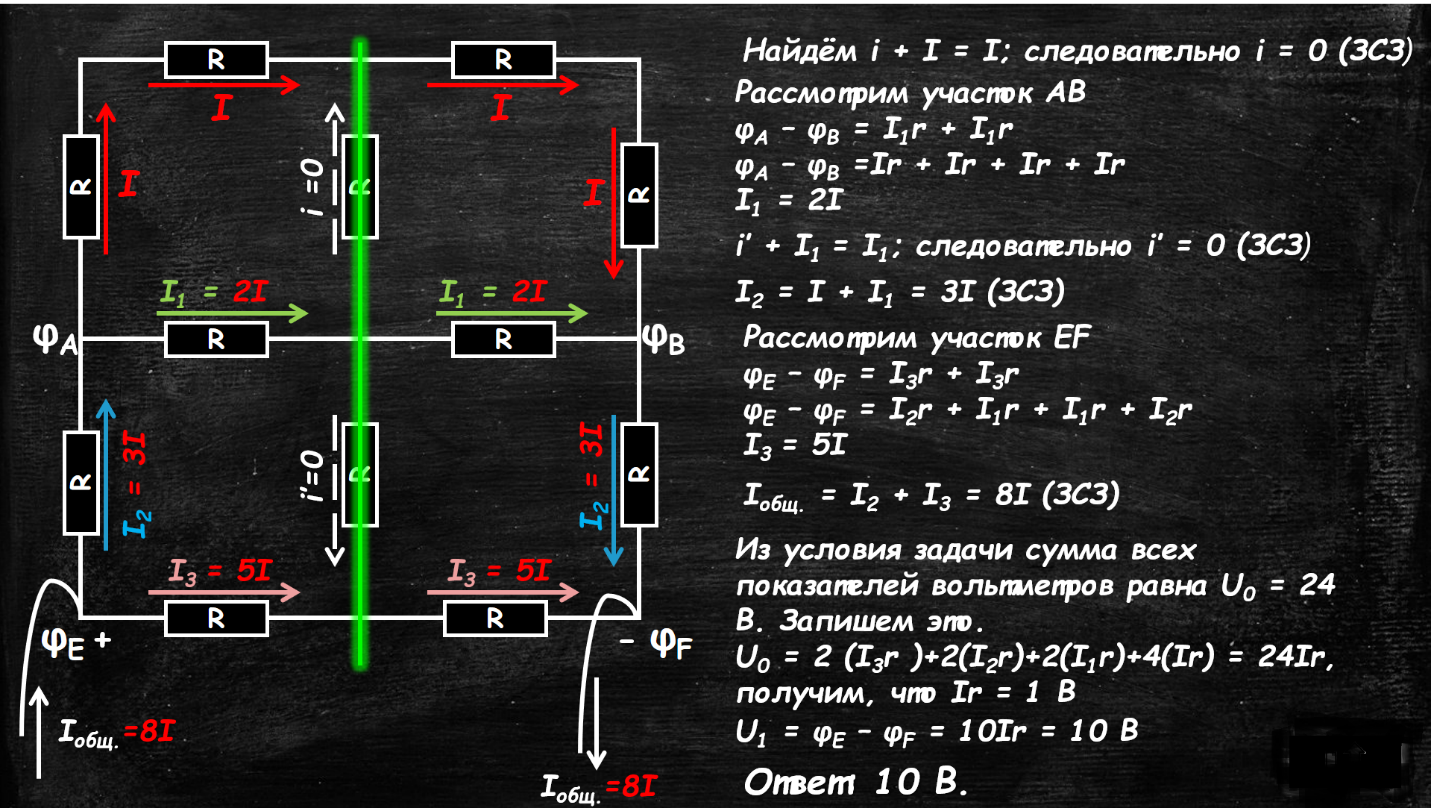
3) примем за 1 ток в самой отдалённой ветви цепи, укажем равные токи в силу симметрии и по закону сохранения заряда и найдём остальные токи
Резисторный куб: Задача Nº3 (автор А. И. Черноуцан)
В каждое из ребер куба включено сопротивление 12 Ом. Чему равно сопротивление получившейся системы при подключении ее соседними вершинами?

Решим эту задачу двумя методами.
1 Метод симметрии (используя «хорошую» и «плохую» симметрии)
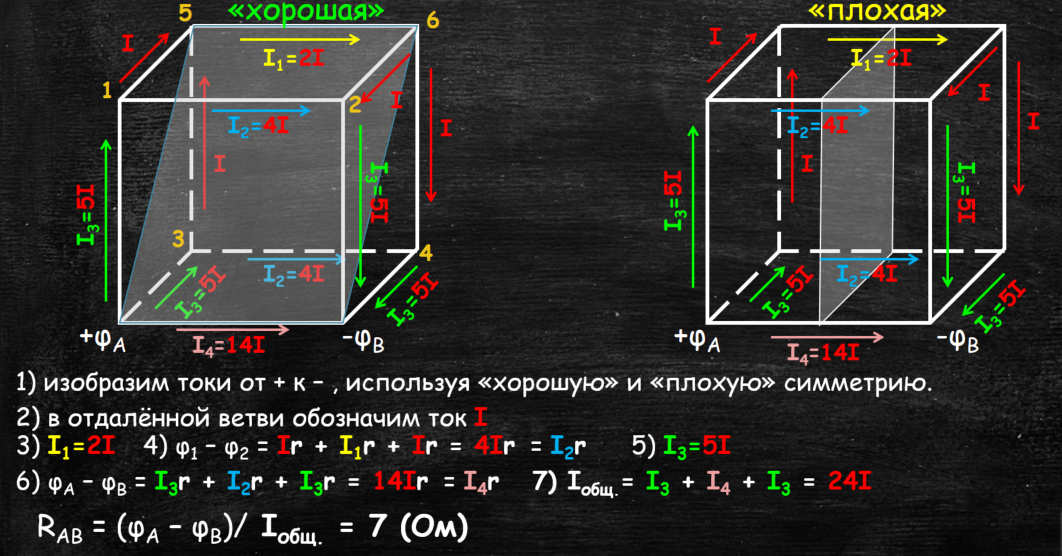
Резисторный куб: Задача Nº3 (автор А. И. Черноуцан)
В каждое из ребер куба включено сопротивление 12 Ом. Чему равно сопротивление получившейся системы при подключении ее соседними вершинами?

Решим задачу методом эквипотенциальных узлов («размножение»). Замени узел О тремя узлами 01,О2 и Оз (эти узлы эквипотенциальны из соображения симметрии). Теперь найти сопротивление цепи не составляет труда.
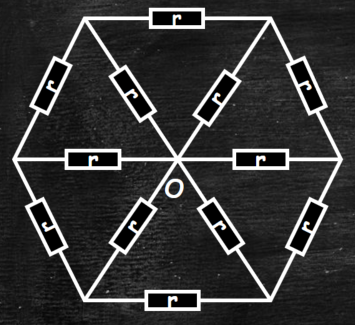

Так же эту задачу можно решить с помощью «хорошей» и «плохой» симметрии. Предлагаю сделать это самостоятельно.
Бесконечная цепь. Задача Nº5 (журнал «Квант»).
Найти сопротивление R участка цепи, содержащего бесконечное число сопротивлений, каждое из которых равно г.

 Если воспользуемся идеей Иоана Тихого, отделить звено резисторов ACDB (это звено далее бесконечно повторяется), то цепь и её сопротивление не изменится (бесконечная часть равна R)
Если воспользуемся идеей Иоана Тихого, отделить звено резисторов ACDB (это звено далее бесконечно повторяется), то цепь и её сопротивление не изменится (бесконечная часть равна R)
Задачи для самостоятельного решения (автор М. А. Пенкин )
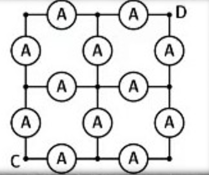 На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых амперметров. К концам С и D этого фрагмента приложили постоянное напряжение U1 = 3,6 В, в результате чего сумма величин показаний всех амперметров составила Io = 48 В. Чему равно внутреннее сопротивление амперметра?
На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых амперметров. К концам С и D этого фрагмента приложили постоянное напряжение U1 = 3,6 В, в результате чего сумма величин показаний всех амперметров составила Io = 48 В. Чему равно внутреннее сопротивление амперметра?
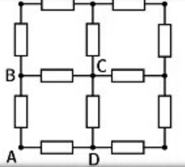 На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых резисторов. Если к точкам А и С подключить омметр, то его показания составят R1 = 21 кОм. Какое сопротивление R2 покажет омметр, если его подсоединить к точкам B и D?
На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых резисторов. Если к точкам А и С подключить омметр, то его показания составят R1 = 21 кОм. Какое сопротивление R2 покажет омметр, если его подсоединить к точкам B и D?
Спасибо за внимание !










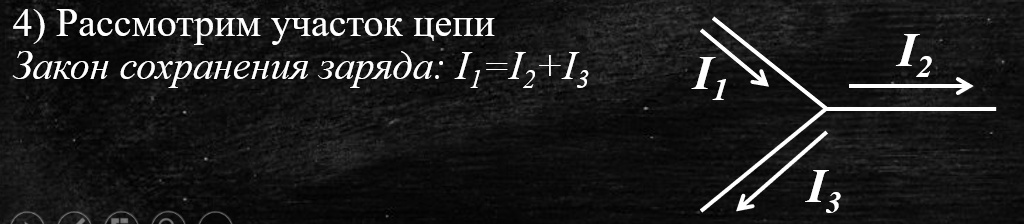



















 Если воспользуемся идеей Иоана Тихого, отделить звено резисторов ACDB (это звено далее бесконечно повторяется), то цепь и её сопротивление не изменится (бесконечная часть равна R)
Если воспользуемся идеей Иоана Тихого, отделить звено резисторов ACDB (это звено далее бесконечно повторяется), то цепь и её сопротивление не изменится (бесконечная часть равна R) На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых амперметров. К концам С и D этого фрагмента приложили постоянное напряжение U1 = 3,6 В, в результате чего сумма величин показаний всех амперметров составила Io = 48 В. Чему равно внутреннее сопротивление амперметра?
На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых амперметров. К концам С и D этого фрагмента приложили постоянное напряжение U1 = 3,6 В, в результате чего сумма величин показаний всех амперметров составила Io = 48 В. Чему равно внутреннее сопротивление амперметра? На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых резисторов. Если к точкам А и С подключить омметр, то его показания составят R1 = 21 кОм. Какое сопротивление R2 покажет омметр, если его подсоединить к точкам B и D?
На рисунке представлена схема фрагмента электрической цепи, состоящего из 12 одинаковых резисторов. Если к точкам А и С подключить омметр, то его показания составят R1 = 21 кОм. Какое сопротивление R2 покажет омметр, если его подсоединить к точкам B и D?









