МЕТОД РАЦИОНАЛИЗАЦИИ
Сущность метода рационализации
(метода замены множителей)
Этот метод наиболее эффективен и доступен для применения к самому широкому классу задач. Он дает возможность рационализировать неравенства с модулем, многие иррациональные неравенства, показательные и логарифмические неравенства как с постоянным, так и с переменным основаниями, а также различные сложные комбинированные неравенства и их системы.
Суть метода рационализации заключается в том, что он позволяет заменять неравенства, состоящие из весьма сложных выражений, на более простые неравенства, решаемые методом интервалов. Единственное ограничение — функции должны быть монотонными.
Необходимо также отметить, что метод рационализации применяется при условии, если исходное неравенство имеет канонический вид:
f1(х) * f2(x)*... * fn(x) v0
g1(x)*g2(x)*...*gm(x)
где знак сравнения v обозначает один из знаков , , fk(x) и gp(x) (k = 1, 2, ... п; р = 1,2,... m) представляют собой различные типы функций.
Решение неравенства зависит только от знаков входящих в него множителей.
1Равносильность неравенств
Два неравенства называются равносильными, если множества их решений совпадают.
Надо учесть, что о равносильности неравенств мы говорим на одном и том же множестве М.
х — 1
![]() Например, неравенства (х - 1)(х - 4)
Например, неравенства (х - 1)(х - 4)
х-4
равносильны (на множестве (-оо; 4) и (4; +оо)).
Множества их решений (1; 4) совпадают. Чтобы убедиться в этом, достаточно решить их методом интервалов.
Аналогично равносильны неравенства log2x log213 и х 13 при условии х 0. Решением каждого из них является множество х 13. При этом первое неравенство логарифмическое, второе — алгебраическое.
Другими словами, решения неравенств log2x - log213 0их-130 совпадают при
х 0. Иначе говоря, при х 0 выражение log2x - log213 имеет такой же знак, что и выражение х - 13. Следовательно, если в каком-либо рассматриваемом неравенстве имеется множитель log2x - log213, то при х 0 его можно заменить на х - 13.
Заметим, что основная часть методов рационализации для различных классов неравенств обусловлена принципом монотонности функций, входящих в неравенства.
2Монотонность функций
Функция у = f(х) называется монотонно возрастающей на данном числовом промежутке X, если для любых двух точек х1 и х2 из промежутка X таких, что х2 X1 = f(х2) f(X1).
Функция у = f(х) называется монотонно убывающей на данном числовом промежутке X, если для любых двух точек х1 и х2 из промежутка X таких, что х2 х1 = f(х2) 1).
Если функция только возрастает или только убывает на данном промежутке, то она называется монотонной на этом промежутке.
3Теорема о корне
Если в уравнении f(х) = С, где С — const, функция у = f(х) непрерывна и монотонна на множестве М, то уравнение имеет на этом множестве М не более одного корня.
Если в уравнении f(х) = g{x) функция у = f(х) непрерывна и строго возрастает, а функция у = g(x) непрерывна и строго убывает на множестве М, то уравнение имеет на М не более одного корня.
Неравенства с модулем
При решении неравенств, содержащих переменную под знаком модуля, методом рационализации, необходимо учитывать условия равносильности:
f(x)0f2(x)0.
f(x)g(x) f2(x)g2(x) ( f(x)- g(x))(f(x) + g(x)) 0.
f(x)≥g(x) f(x) - g(x) ≥ 0
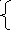
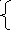
g(x)

f(x)- g(x)0 (f(x) - g(x))(f(x) + g(x)) ≥0,
 для всех x
для всех x 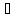 D(f) D(g).
D(f) D(g).
4. f(x) ≤ g(x) f(x) - g(x) ≤
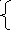 g(x) ≥0,
g(x) ≥0,
( f(x)- g(x))(f(x) + g(x)) ≤0.
5. ( f(x)- g(x)) h(x) 0 (f(x)-g(x))(f(x)+g(x))*h(x) 0.
h(x) 0 (f(x)-g(x))(f(x)+g(x))*h(x) 0.
Примеры с решениями
Пример 1. Решить неравенство
x2 - 13x + 1 ≤ x2 + 6x - 11.
Решение.
Применяя условие 2 (f(x)g(x) f2(x)g2(x) ( f(x)- g(x))(f(x) + g(x)) 0 ), имеем (x2 - 13x+1- x2 - 6x + 11)( x2 - 13x+1+ x2 + 6x - 11) ≤0, или
(-19x+12)(2 x2 - 7x - 10) ≤0, или (19x - 12)(2 x2 - 7x-10) ≥0.
Неравенство (1) решим методом интервалов:
Нули: 19х - 12 = 0, 2 x2 - 7x - 10 = 0,
12
![]() х 1 = . D = 49 + 80 = 129 0
х 1 = . D = 49 + 80 = 129 0
19
7 ± √129
![]() x2,3 = .
x2,3 = .
4
Расположим полученные корни на числовой прямой, учитывая, что
7 - √129 12 7 + √129
![]()
![]()
![]() √129 ≈ 11,4
√129 ≈ 11,4
4 19 4
- + - +
 •/////////////• •/////////
•/////////////• •/////////
7 - √129 12 7 + √129
![]()
![]()
![]()
 4 19 4
4 19 4





![]() 7 - √129 12 7 + √129
7 - √129 12 7 + √129
![]()
![]() Ответ: ; ; + ∞
Ответ: ; ; + ∞
4 19 4
Пример 2. Решить неравенство :
![]()
![]()
![]() х2 - 3х + 2
х2 - 3х + 2
- 1 ≤ 0.
х2 + 3х + 2
Неравенство (1) равносильно смешанной системы

x2 - 3x + 2 - x2 + 3x + 2 ≤ 0
x2 + 3x + 2 ≠ 0.
 Следовательно,
Следовательно,
( x2 - 3x + 2 - x2 - 3х - 2)( x2 - 3x + 2 + x2 + 3х + 2) ≤ 0,
(х + 1)(х+2) ≠ 0.
 -6х(2х2 + 4) ≤ 0,
-6х(2х2 + 4) ≤ 0,
или
х ≠ -1, х ≠ -2.

Разделив обе части неравенства на (-12), получим х(х2 + 2) ≥ 0,
х ≠ -1, х ≠ -2.
 Поскольку x2 + 2 0 при всех х
Поскольку x2 + 2 0 при всех х 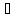 R, то имеем
R, то имеем
х ≥ 0
откуда х ≥ 0, т.е. х 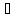 [0; + ∞).
[0; + ∞).
х ≠ -1, х ≠ -2,
Ответ: [0; + ∞)
Пример 3. Решить неравенство
x2 + x - 12 - 45 ≤ 9 x - 3 - 5x + 4.
Решение.
Поскольку x2 + x - 12 = (x - 3)(х+4), где 3 и 4 корни трёхчлена и a b = a
b = a  b, то исходное неравенство примет вид х+4х-3 - 45 ≤ 9 x - 3 - 5x + 4, или
b, то исходное неравенство примет вид х+4х-3 - 45 ≤ 9 x - 3 - 5x + 4, или
(х+4х-3 - 9x - 3) + 5(x + 4 - 9) ≤ 0, или
x - 3  (х+4 - 9) +5(х+4 - 9) ≤ 0.
(х+4 - 9) +5(х+4 - 9) ≤ 0.
Остается вынести за скобки общий множитель (х+4 - 9)( x - 3 + 5) ≤ 0. (1)
Неравенство (3) мы привели к виду, при котором можно использовать условие равносильности 2:(f(x)g(x) f2(x)g2(x) ( f(x)- g(x))(f(x) + g(x)) 0).
(х + 4 - 9)(х + 4 + 9)(х - 3 - 5)(х - 3 + 5) ≤ 0, или (х - 5)(х+13)(х - 8)(х + 2) ≤ 0.
Решаем методом интервалов, имеем
+ - + - +
 •/////////• •////////////•
•/////////• •////////////•
-13 -2 5 8
 х € [-13; -2] [5; 8].
х € [-13; -2] [5; 8].
 Ответ: [-13; -2] [5; 8].
Ответ: [-13; -2] [5; 8].
7х - 2 - х - 9
![]() Пример 4. Решить неравенство ) ≤ 0.
Пример 4. Решить неравенство ) ≤ 0.
4х - 3 - х + 3
Решение.
Используя метод рационализации, получим
(7х - 2 - х + 9)(7х - 2 + х -9) (6х + 7)(8х -11) (6х + 7)(8х-11)
![]()
![]()
![]() ≤ 0, или ≤ 0, или ≤ 0. (1)
≤ 0, или ≤ 0, или ≤ 0. (1)
(4х - 3 - х -3)(4х - 3 + х + 3) 3(х - 2)*5х х(х-2)
Кроме того, 4х - 3≠х+3, т.е. 4х-3≠ ±(х+3), откуда х ≠ 2, х ≠ 0.
Теперь остается решить неравенство (4) методом интервалов.
+ - + - +
 •///////////////◦ •///////////////◦
•///////////////◦ •///////////////◦
![]()
![]()
![]() 7 0 11 2
7 0 11 2
6 8



 7 11
7 11
![]()

![]()
![]() Значит, х ɛ ; 0 ; 2 .
Значит, х ɛ ; 0 ; 2 .
6 8




 7 11
7 11
![]()
![]()
![]() Ответ: ; 0 ; 2 .
Ответ: ; 0 ; 2 .
6 8
74 - х
![]() Пример 5. Решить неравенство - х - 4 ≤ 0.
Пример 5. Решить неравенство - х - 4 ≤ 0.
13 - х + 3
Решение.
Поскольку -х = х, то данное неравенство можно записать в виде

 7 х - 4(7 - 13 + х+3) х - 4(х+3 - 6
7 х - 4(7 - 13 + х+3) х - 4(х+3 - 6
![]()
![]()
![]() х-4
х-4  - 1 ≤ 0, или ≤ 0, или ≥ 0. (1)
- 1 ≤ 0, или ≤ 0, или ≥ 0. (1)
13 - х + 3 13 - х+3 х+3 - 13
Нетрудно заметить, что х = 4 ─ решение неравенства (1), а значит, и исходного.
х + 3 - 6
![]() Теперь решим методом рационализации неравенство ≥ 0, используя условие
Теперь решим методом рационализации неравенство ≥ 0, используя условие
х + 3 - 13
равносильности 3.
(х + 3 - 6)(х + 3 + 6) (х - 3)(х+9)
![]()
![]() ≥ 0, или ≥ 0, х = 4.
≥ 0, или ≥ 0, х = 4.
(х + 3 - 13)(х + 3 + 13) (х - 10)(х + 16)
+ - + - - +
 //////////◦ •/////////////////• • ◦//////
//////////◦ •/////////////////• • ◦//////
-16 -9 3 4 10


 Знчит, х
Знчит, х 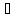 (-∞; -16) [-9; 3] {4} (10; +∞).
(-∞; -16) [-9; 3] {4} (10; +∞).


 Ответ: (-∞; -16) [-9; 3] {4} (10; +∞).
Ответ: (-∞; -16) [-9; 3] {4} (10; +∞).
x2 - 5х + 6 - x2 + 7х - 8
![]() Пример 6. Решить неравенство ≥ 0.
Пример 6. Решить неравенство ≥ 0.
6х-1 - 2х-9
Решение.
(x2 - 5х + 6 - x2 -7х + 8)( x2 - 5х + 6 + x2 +7х - 8) (-12х + 14)(2х2 + 2х - 2)
![]()
![]() ≥ 0, или ≥ 0.
≥ 0, или ≥ 0.
(6 - 1 - 2х + 9)(6х - 1 + 2х - 9) (4х + 8)(8х - 10)
После упрощения получим
(6х - 7)( х2 + х - 1)
![]() ≤ 0. (1)
≤ 0. (1)
(х + 2)(4х - 5)
7 -1 ± √5
![]()
![]() Корни числителя: х1 = , х2,3 = .
Корни числителя: х1 = , х2,3 = .
6 2
5
![]() Корни знаменателя: х4 = -2, х5 = .
Корни знаменателя: х4 = -2, х5 = .
4
- 1 + √5 7
![]()
![]() Заметим, что √5 ≈ 2,24, тогда х1 5,
Заметим, что √5 ≈ 2,24, тогда х1 5,
2 6
Решим неравенство (1) методом интервалов.
- + - + - +
 ////////◦ •//////////////////////• • /////////◦
////////◦ •//////////////////////• • /////////◦
-2 -1-√5 -1+√5 7 5
2 2 6 4



 -1 - √5 -1 + √5 7 5
-1 - √5 -1 + √5 7 5

![]()
![]()
![]()
![]()
 х
х 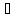 (-∞; -2) ; ; .
(-∞; -2) ; ; .
2 2 6 4




 -1 - √5 -1 + √5 7 5
-1 - √5 -1 + √5 7 5
![]()
![]()
![]()
![]()
 Ответ: (-∞; -2) ; ; .
Ответ: (-∞; -2) ; ; .
2 2 6 4
Пример 7. Решить неравенство 3х2 - 4х - 4 ≤ 2х2 - 6х + 8.
Решение.
Запишем неравенство в виде 3х2 - 4х - 4 - 2х2 - 12х + 16 ≤ 0.
Так как х2 = х2, то имеем 3х2 - 4х - 4 - 2х2 - 12х + 16 ≤ 0.
Теперь применим метод рационализации: (3х2 - 4х - 4 - 2х2 + 12х - 16)(3х2 - 4х - 4 + 2 х2 -
- 12х +16) ≤ 0, или (х2 + 8х - 20)(5х2 - 16х + 12) ≤ 0.
Используя формулу ax2 + bx + c = a(x - x1)(x - x2), где x1 и x2 ─ корни трехчлена, разложим каждый из квадратных трехчленов относительно х на линейные множители:
(х + 10)( х - 2)(5х - 6)(х - 2) ≤ 0. Так как х + 10 0 при всех х 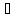 R, то получим
R, то получим

 х = 2 х = ±2
х = 2 х = ±2
(х - 2)2(5х - 6) ≤ 0, откуда или
5х - 6 ≤ 0, (5х - 6)(5х + 6) ≤ 0 .
+ + - + +
 • •////////////////• •
• •////////////////• •
-2 -1,2 1,2 2

 Следовательно, х
Следовательно, х 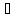 {-2} [-1,2; 1,2] {2}.
{-2} [-1,2; 1,2] {2}.

 Ответ: {-2} [-1,2; 1,2] {2}.
Ответ: {-2} [-1,2; 1,2] {2}.
||х2 - 3х| - 5|-5
![]() Пример 8. Решить неравенство ≥0.
Пример 8. Решить неравенство ≥0.
||8х - 7| - 7| - 9
Решение.
Применяя метод рационализации, получим
(|х2 - 3х| - 5 - 5)(|х2 -3х| - 5+5) (|х2 - 3х| - 10)|х2 -3х|
![]()
![]() ≥0, или ≥0.
≥0, или ≥0.
(|8х - 7| - 7 - 9) (|8х - 7| - 7 + 9) (|8х - 7| - 16) (|8х - 7| + 2)
Заметим, что |8х - 7| + 2 0 при всех х 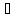 R. Тогда полученное неравенство равносильно смешанной системе
R. Тогда полученное неравенство равносильно смешанной системе
 |х2 - 3х| - 10
|х2 - 3х| - 10
![]() ≥0,
≥0,
|8х - 7| - 16
х2 - 3х = 0.
К неравенству системы ещё раз применим метод рационализации

 (х2 - 3х - 10)( х2 - 3х + 10) (х-5)(х+2)(х2 -3х + 10)
(х2 - 3х - 10)( х2 - 3х + 10) (х-5)(х+2)(х2 -3х + 10)
![]()
![]() ≥ 0, или ≥0,
≥ 0, или ≥0,
(8х - 7 -16)(8х - 7 + 16) (8х - 23)(8х + 9)
х(х - 3) = 0, х = 0, х=3.
Учитывая, что х2 - 3х + 10 0 при всех х 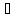 R, так как D a =1 0, получим
R, так как D a =1 0, получим
 (х-5)(х+2)
(х-5)(х+2)
![]() ≥ 0,
≥ 0,
(8х - 23)(8х + 9)
х=0, х=3. Остаётся решить полученное неравенство методом интервалов и добавить числа 0 и 3.
+ - + + - - +
 ///////• ◦///////////•///////////◦ • •////////
///////• ◦///////////•///////////◦ • •////////
-2 - 9 0 23 3 5
8 8

 9 23
9 23


![]()
![]()
 х
х 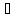 (-∞; -2] - ; {3} [5; + ∞).
(-∞; -2] - ; {3} [5; + ∞).
8 8
9 23
![]()
![]()



 Ответ: (-∞; -2] - ;
Ответ: (-∞; -2] - ;  {3} [5; + ∞).
{3} [5; + ∞).
8 8
||5х2 - х| - 3|-5х2 - х - 8
![]() Пример 9. Решить неравенство ≥ 0 и указать наименьшее
Пример 9. Решить неравенство ≥ 0 и указать наименьшее
|х - 2 - х2| - х2 + 4х - 6
целое решение.
Решение.
||5х2 - х| - 3|-(5х2 + х + 8)
![]() Запишем неравенство в виде ≥ 0. (1)
Запишем неравенство в виде ≥ 0. (1)
|х - 2 - х2| - (х2 - 4х + 6)
Заметим, что 5х2 + х + 8 0 при всех х 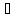 R, так как D 0.
R, так как D 0.
Аналогично х2 - 4 х + 6 0 при всех х 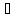 R. Тогда неравенство (1) примет вид
R. Тогда неравенство (1) примет вид
||5х2 - х| - 3|-|5х2 + х + 8|
![]() ≥ 0. (2)
≥ 0. (2)
|х - 2 - х2| - |х2 - 4х + 6|
Теперь к неравенству (2) применим метод рационализации
(|5х2 - х| - 3-(5х2 + х + 8))(|5х2 - х| - 3 + (5х2 + х + 8))
![]() ≥ 0, или
≥ 0, или
(х - 2 - х2 - х2 + 4х - 6)(х - 2 - х2 + х2 - 4х + 6)
(|5х2 - х| - (5х2 + х + 11))(|5х2 - х| + (5х2 + х + 5))
![]() ≥ 0.
≥ 0.
(2х2 - 5х + 8)(3х - 4)
Но 5х2 + х + 5 0 при всех х 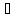 R и |5х2 - х| ≥ 0, тогда |5х2 - х| + (5х2 + х + 5) 0.
R и |5х2 - х| ≥ 0, тогда |5х2 - х| + (5х2 + х + 5) 0.
Аналогично 2х2 - 5х + 8 0 при всех х 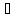 R. Полученное неравенство равносильно неравенству
R. Полученное неравенство равносильно неравенству
|5х2 - х| - (5х2 + х + 11)
![]() ≥ 0. (3)
≥ 0. (3)
3х-4
Так как 5х2 + х + 11 0 при всех х 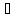 R, то 5х2 + х + 11 = |5х2 + х + 11|. Тогда неравенство (3) запишется в виде
R, то 5х2 + х + 11 = |5х2 + х + 11|. Тогда неравенство (3) запишется в виде
|5х2 - х| - |5х2 + х + 11|
![]() ≥ 0.
≥ 0.
3х - 4
Вновь применив метод рационализации, получим
(5х2 - х - 5х2 - х - 11)( 5х2 - х + 5х2 + х + 11) -(2х + 11)(10х2 + 11)
![]()
![]() ≥ 0, или ≥ 0.
≥ 0, или ≥ 0.
3х - 4 3х-4
Поскольку 10х2 + 11 0 при всех х 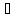 R, то получим равносильное неравенство
R, то получим равносильное неравенство
2х + 11
![]() ≤ 0. (4)
≤ 0. (4)
3х - 4
11 4
![]()
![]() Наконец, решаем неравенство (4) методом интервалов, находим х1 = - , х2 = .
Наконец, решаем неравенство (4) методом интервалов, находим х1 = - , х2 = .
2 3
+ - +
 •////////////////◦
•////////////////◦
-11 4

 2 3
2 3
11 4
![]()
![]() х
х 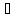 - ; .
- ; .
2 3
Тогда х = - 5 ─ наименьшее целое решение неравенства (4), а значит, и исходного.
Ответ: - 5.
(|3х - 4| - 1)(|6 - х2| - 13)
![]() Пример 10. Решить неравенство ≤ 0 и указать наибольшее
Пример 10. Решить неравенство ≤ 0 и указать наибольшее
(х - 7)2 + |х - 7| - 30
целое решение.
Решение.
Так как |6 - х2| = |х2 - 6| и (х - 7)2 = |х - 7|2 , то данное неравенство примет вид
(|3х - 4| - 1)(|х2 - 6| - 13)
![]() ≤ 0. (1)
≤ 0. (1)
|х - 7|2 + |х - 7| - 30
Знаменатель дроби неравенства (1) представляет собой квадратный трехчлен относительно |х - 7|, корни которого 5 и -6.
Следовательно, неравенство (1) можно записать в виде
(|3х - 4| - 1)(|х2 - 6| - 13)
![]() ≤ 0. (2)
≤ 0. (2)
(|х - 7| - 5)( |х - 7| + 6)
Но │х-7│+ 6 0 при всех х 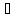 R, тогда получим равносильное неравенство
R, тогда получим равносильное неравенство
 которое решим методом рационализации:
которое решим методом рационализации:

Так как x2+70 при всех х

X1=1: X2 = : X3=-
: X3=- :X4=
:X4= : X5=12: X6=2.
: X5=12: X6=2.

 х
х 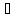 (-
(- ; 1] [
; 1] [  :2) [
:2) [ 12).
12).







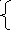

 для всех x
для всех x 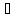 D(f) D(g).
D(f) D(g). h(x) 0 (f(x)-g(x))(f(x)+g(x))*h(x) 0.
h(x) 0 (f(x)-g(x))(f(x)+g(x))*h(x) 0. •/////////////• •/////////
•/////////////• •/////////  4 19 4
4 19 4






















