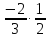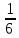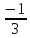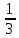23
Пояснительная записка
Математическое образование — это испытанное столетиями средство интеллектуального развития в условиях массового обучения. Изучение математики в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта.
2) в метапредметном направлении:
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
формирование представлений о математике как части общечеловеческой культуры, о значимости математики и развитии цивилизации и современного общества.
3) в предметном направлении:
овладение математическими знаниями и умениями, необходимыми для применения в повседневной жизни, изучения смежных дисциплин, продолжения обучения в старшей школе или иных формах среднего образования;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Изучение математики в 5 – 6 классах способствует приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
В ходе наблюдения я пришла к выводу, что учащиеся часто сталкиваются с проблемой: как выполнить действия с рациональными числами. В процессе обучения ребятам неоднократно приходится встречаться с рациональными числами (решение уравнений и неравенств, решение систем уравнений и неравенств, действия с одночленами и многочленами, преобразование алгебраических выражений). И вот тут возникает масса проблем. Учащиеся не понимают, почему над рациональными числами совершаются действия по таким – то правилам, а не по иным. В частности, почему при умножении и делении положительных и отрицательных чисел получаются именно такие знаки. Учащиеся неверно выполняют действия (заменяют одно действие другим), «теряют» знаки или наоборот ставят там, где не нужно. Поэтому проблема надежного и четкого усвоения действий с рациональными числами является актуальной.
Я считаю, что в 6 классе необходимо приложить все усилия для того чтобы ребёнок не только запомнил правила действий с рациональными числами, но и умел грамотно применять эти правила при решении заданий. В связи с этим соответствующий учебный материал должен быть представлен в наиболее доступном для каждого ученика виде.
Изучение раздела программы «Действия с рациональными числами» позволяет наиболее подробно рассмотреть понятие рационального числа и действий, связанных с ним. С первых дней занятий стоит задача творческого поурочного и тематического планирования тем и разделов предмета, использования дополнительных дидактических материалов и методическо — психологических приемов.
После изучения данного раздела ребята должны владеть приёмами действий с рациональными числами. Они должны научиться выполнять задания, применив наиболее удобный для них способ, овладеть приёмами устного счёта.
Использование различных форм организации учебной деятельности повышает интерес к изучению данного раздела, формирует познавательный интерес, что способствует самообразованию.
Применение на уроках презентационного сопровождения позволяет сформировать необходимые понятия. Посредством таких уроков активизируются психические процессы учащихся: восприятие, память, мышление, внимание. Дети с увлечение работают на уроках, «открывают» новые для них понятия и правила.
Методическая разработка составлена на основе программы по математике для общеобразовательных школ 5 – 6 классы, автор – составитель В.И.Жохов. Программа составлена в соответствии с требованиями образовательного стандарта по математике и полностью реализует федеральный и региональный компонент основного общего образования. Основу учебно- методического комплекса составляют:
Учебник: Математика 6 класс. Авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. М. Мнемозина, 2011.
Учебные пособия: Дидактические материалы по математике для 6 класса / А.С. Чесноков, К.И. Нешков. – 6-е изд. – М.: Просвещение, 2009, - 144 с.: ил.;
В.И. Жохов, Л.Б. Крайнева. Математика. Контрольные работы 6 класс. М., « Мнемозина», 2012г.
Методические пособия: Преподавание математики в 5 и 6 классах: По учебникам: Математика Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. /Методические рекомендации для учителя./ – 2-е изд. – М.: Вербум-М
В.И. Жохов. Математический тренажор. 6 класс. М., « Мнемозина», 2012г.
В.И. Жохов, Л.Б. Крайнева. Математика. Контрольные работы 6 класс. М., « Мнемозина», 2012г.
И.Б. Шестакова. Математика 6 класс. Контрольные работы в новом формате. М., «Интелект-Центр», 2011г.
2. Цели и задачи изучения раздела
«Действия с рациональными числами»
Раздел программы по математике «Действия с рациональными числами решает ряд целей и задач обучения:
Цели:
Выработать навыки вычисления с рациональными числами, сочетая устные и письменные приемы вычислений;
Научить использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации прием;
Формировать способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Задачи:
1. Познавательная:
продолжить формирования центральных математических понятий;
знание и правильное употребление терминов, связанных с рациональными числами;
выработать навыки складывать рациональные числа с помощью координатной прямой;
формировать логическую культуру учащихся, связанную с процессом выполнения действий с рациональными числами;
выработать прочные навыки арифметических действий с положительными и отрицательными числами.
2. Развивающая:
подвести учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, пониманию математики как части общей культуры человечества;
развить интеллектуальные и творческие способности учащихся, познавательную активность, интерес к изучению математики;
овладеть математическими знаниями и умениями, необходимыми для применения в повседневной жизни.
3. Воспитательная:
воспитать качества личности, формируемые в ходе учебной математической деятельности и обеспечивающие социальную мобильность, творческую активность, способность принимать самостоятельные решения.
3.Психолого – педагогическое объяснение специфики восприятия учебного материала учащимися в соответствии с возрастными особенностями
Согласно стандарту общего математического образования, курс «Действия с рациональными числами» изучается в 6 классе. Возраст шестиклассников 11 – 13 лет. Этот период относят к подростковому возрасту, некоторые психологи выделяют его отдельно в, так называемый, младший подростковый возраст. Знание и использование в педагогической практике резервов развития младших подростков помогает более успешно обучать и воспитывать детей. Чаще всего приходиться решать проблемы: как сформировать положительную учебную мотивацию, развивать познавательную учебную мотивацию, развивать познавательную и творческую активность, увлечь, заинтересовать, пробудить интерес. Учеными и практиками затрачиваются колоссальные усилия для их разрешения. Но почему-то установилась печальная закономерность: чем дальше идет процесс обучения, тем ниже активность учеников. Чтобы избежать превращения школьника в потребителя знаний необходимо постоянно учитывать возрастные особенности школьников.
Подростковый возраст – это возраст “пытливого ума, жадного стремления к познанию, возраст кипучей энергии, бурной активности, инициативности, жажды деятельности”. Поведение и деятельность подростка во многом определяются особенностями самооценки. В учебной деятельности подростка имеются свои трудности и противоречия, но есть и свои преимущества, на которые может и должен опираться педагог. Эти особенности подростков учитываются в преподавании раздела через проведение работы по осознанию подростком личностного смысла изучаемой темы. Шестиклассники ещё находятся в начальном подростковом периоде, поэтому легко идут на контакт с учителем и сверстниками, их можно заинтересовать занимательным изложением материала, его практической значимостью.
С общим ростом сознательного отношения к действительности заметно усиливается сознательное отношение к учению. С другой стороны, именно в подростковом возрасте наблюдаются отдельные случаи отрицательного отношения к учению: в каждом конкретном случае я стараюсь выяснить причины такого отношения. Одной из таких причин является своеобразная реакция подростка на те или иные неудачи в учении, вызванные иногда случайными обстоятельствами (например, болезнью), ведущие к снижению успеваемости.
Подросток обычно остро переживает собственные неудачи, и затронутое самолюбие вызывает у него желание замаскировать свое подлинное отношение к этим неудачам: он делает вид, что успехи в учении не имеют для него значения. Поэтому я вовлекаю таких детей в посильную деятельность, поручаю выполнение индивидуального задания с последующей положительной оценкой, создаю ситуацию успеха.
К индивидуальным различиям в умственных способностях относятся и способности учащихся к самостоятельному приобретению знаний, умений самостоятельной работы. Они связаны со всей познавательной деятельностью ученика: овладение новыми знаниями, выполнение различных учебных практических заданий, особенно выделение в изучаемом материале существенного, установления связи нового материала с ранее усвоенным и т.п. Для учащихся, имеющих затруднения при выполнении самостоятельной работы, принимаю меры, соответствующие каждому конкретному случаю. Это может быть разделение сложной задачи на этапы, помощь ученикам в составлении плана ответа. Стремлюсь к тому, чтобы выработать у учащихся навыки обобщать, делать выводы, выделять наиболее главное и т.п.
В подростковом возрасте изменяется мышление школьника, оно приобретает новые черты и качества. Согласно теории И.Я. Каплуновича в структуру математического мышления входят пять пересекающихся подструктур: топологическая, проективная, порядковая, метрическая и алгебраическая (композиционная) – которые складываются постепенно, и в ходе развития интеллекта ребенка каждая из этих подструктур может занимать ведущее место. Топологическая подструктура мышления обеспечивает замкнутость, компактность, связанность осуществляемых мышлением преобразований, непрерывность трансформаций, мысленное выращивание, вылепливание в представлении требуемого объекта (его образа). Порядковая подструктура мышления дает возможность постоянного сопоставления человеком математических объектов и их элементов по таким характеристикам, как больше - меньше, ближе - дальше, часть - целое, изменение направления движения и его характера, положение, форма, конструкция предмета. Метрические подструктуры мышления позволяют вычленять в объектах и их компонентах количественные величины и отношения (пропорции, численные значения размеров, углов, расстояний). Алгебраические структуры мышления помогают осуществлять не только прямые и обратные операции над математическими объектами, расчленение и соединение их составляющих, но и замену нескольких операций, объединение нескольких блоков предмета в один, выполнение математических преобразований в любой последовательности. Проективные подструктуры мышления обеспечивают изучение математического объекта или его изображения с определенного самостоятельно выбранного положения, проецирование с этой позиции объекта на изображение (или изображения на объект) и установление соответствия между ними.
В соответствии со своей ведущей подструктурой ученик по – разному воспринимает, оперирует, перерабатывает и воспроизводит математическую информацию 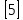 .
.
Внимание подростков постепенно приобретает характер организованных, регулируемых и управляемых процессов. Внимание само по себе не является особым познавательным процессом. Оно присуще любому познавательному процессу (восприятию, мышлению, памяти и т.д.) и выступает как форма, способность организации этого процесса. В подростковом возрасте человек становится изобретательным, анализирующим и восприимчивым.
Значительно увеличивается объем памяти, причем не только за счет лучшего запоминания материала, но и его логического осмысления. Усиливается стремление добиваться понимания того, что надо запомнить, и воспроизводить не буквально, а своими словами, делая при этом нужные сохранения и обобщения. Свойства памяти у каждого ребенка различны. Одни сразу же могут воспроизвести правила, определения и т.д. Другие на этапе первичного ознакомления с материалом этого сделать не могут (не потому что не хотят, а именно не могут). Таким ученикам надо еще некоторое время для осмысления, запоминания. Учитывая свойства памяти, мышления, таких учащихся спрашиваю не сразу, после ознакомления с новым материалом, а через урок, может быть два, давая им необходимое время. Но к концу изучения темы, конечно, все учащиеся должны знать и уметь формулировать основные понятия.
“Активность младшего подростка не та, что у младших школьников. Его привлекает теперь не столько сам процесс деятельности, сколько цель и ее результат. Он уже не просто собирает макулатуру или приводит в порядок библиотечные книги, а стремится сделать это как можно лучше, не просто любит читать, а выбирает самые “героические” книги, те, в которых описаны подвиги, приключения. Он становится мечтателем, романтиком. Он углублен в свои переживания, интересы. Он, то энергичен, деятелен, весел, то вдруг вял, пассивен, мрачен” – пишет кандидат педагогических наук В. Лапик. Задача педагогов состоит в том, что бы создать педагогическое пространство, где ребенок имел бы возможность для разностороннего проявления своей личности, обогащения своего внутреннего мира – основа, на базе которой формулируется и развивается творческий процесс.
4. Ожидаемые результаты освоения раздела
«Действия с рациональными числами»
В результате изучения раздела «Действия с рациональными числами» ученик:
учится складывать и вычитать рациональные числа с помощью координатной прямой;
знает правила сложения и вычитания чисел рациональных чисел и умеет применять их в процессе вычисления;
знает правила действий умножения и деления рациональных чисел и умеет применять их на практике;
знает свойства действий с рациональными числами и умеет применять их для упрощения вычислений;
дополняет свои знания о числе;
овладевает основами культуры математического мышления;
планирует и осуществляет алгоритмическую деятельность, выполняет заданные и конструирует новые алгоритмы;
исследует, проводит эксперименты, обобщает, ставит и формулирует новые задачи;
ясно, точно, грамотно излагает свои мысли в устной и письменной речи, использует различные языки математики (словесный, символический, графический), свободно переходит с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
систематизирует, анализирует и классифицирует информацию, использует разнообразие информационных источников, включая учебную и справочную литературу, современные информационные технологии;
владеет навыками самостоятельной познавательной деятельности;
видит применение изучаемого материала в практической деятельности.
5. Обоснование используемых в образовательном процессе по разделу программы образовательных технологий, методов, принципов и форм организации учебной деятельности учащихся.
5.1. Использование информационно-коммуникационных технологий в образовательном процессе.
Ранее информацию по любой теме ребенок мог получить по разным каналам: учебник, справочная литература, лекция учителя, конспект урока. Но, сегодня, учитывая современные реалии, учитель должен вносить в учебный процесс новые методы подачи информации.
Необходимо научить каждого ребенка за короткий промежуток времени осваивать, преобразовывать и использовать в практической деятельности огромные массивы информации. Очень важно организовать процесс обучения так, чтобы ребенок активно, с интересом и увлечением работал на уроке, видел плоды своего труда и мог их оценить.
Помочь учителю в решении этой непростой задачи может сочетание традиционных методов обучения и современных информационных технологий, в том числе и компьютерных. Ведь использование компьютера на уроке позволяет сделать процесс обучения мобильным, строго дифференцированным и индивидуальным.
Предполагается большая подготовительная работа при составлении уроков, но в итоге можно получить эффективную и универсальную систему обучения и проверки знаний. Компьютер может использоваться на всех этапах – как при подготовке к уроку, так и в процессе обучения: при объяснении (введении) нового материала, закреплении, повторении, контроле ЗУН.
Преимущества использования ИКТ:
1. Индивидуализация обучения;
2. Интенсификация самостоятельной работы учащихся;
3. Рост объема выполненных на уроке заданий;
4.Повышение мотивации и познавательной активности за счет разнообразия форм работы, возможности включения игрового момента. Такое занятие вызывает у детей эмоциональный подъем, даже отстающие ученики охотно работают на уроке.
5. Интегрирование обычного урока с компьютером позволяет переложить часть своей работы на ПК, делая при этом процесс обучения более интересным, разнообразным, интенсивным.
В частности, становится более быстрым процесс записи определений и других важных частей материала, так как не приходится повторять текст несколько раз (он выводится на экран), ученику не приходится ждать, пока повторят именно нужный ему фрагмент.
6. Применение на уроке компьютерных тестов и диагностических комплексов позволяет за короткое время получать объективную картину уровня усвоения изучаемого материала у всех учащихся и своевременно его скорректировать.
7. Для ученика важно то, что сразу после выполнения теста (когда эта информация еще не потеряла свою актуальность) он получает объективный результат с указанием ошибок, что невозможно, например, при устном опросе.
При объяснении нового материала на уроке можно использовать иллюстрации, фотографии, портреты, таблицы и схемы, проектируя их на большой экран. При этом существенно меняется технология объяснения – можно комментировать информацию, появляющуюся на экране, по необходимости сопровождая ее дополнительными объяснениями и примерами.
8. Использование интерактивной доски соответствует способу восприятия информации, свойственному нынешним школьникам, многие из которых испытывают потребность в визуализации информации. Благодаря наглядности и интерактивности удается активизировать работу учащихся и поддерживать у них интерес к предмету. У ребят повышается внимание, они лучше понимают и запоминают материал.
5.2. Методы обучения по источнику получения знаний.
Словесные методы обучения.
Словесные методы занимают ведущее место в системе методов обучения. Словесные методы позволяют в кратчайший срок передать большую по объему информацию, поставить перед обучаемыми проблемы и указать пути их решения. С помощью слова можно вызвать в сознании детей яркие картины прошлого, настоящего и будущего человечества. Слово активизирует воображение, память, чувства учащихся.
Объяснение.
Объяснение как метод обучения широко используется в работе с детьми разных возрастных групп. Однако в среднем и старшем школьном возрасте, в связи с усложнением учебного материала и возрастающими интеллектуальными возможностями учащихся, использование этого метода становится более необходимым, чем в работе с младшими школьниками.
Эвристическая беседа.
Широкое распространение имеет эвристическая беседа (от слова “эврика” нахожу, открываю). В ходе эвристической беседы, опираясь на имеющиеся у учащихся знания и практический опыт, можно подвести их к пониманию и усвоению новых знаний, формулированию правил и выводов.
Наглядные методы.
Под наглядными методами обучения понимаются такие методы, при которых усвоение учебного материала находится в существенной зависимости от применяемых в процессе обучения наглядного пособия и технических средств. Наглядные методы используются во взаимосвязи со словесными и практическими методами обучения.
Метод иллюстраций предполагает показ ученикам иллюстративных пособий, плакатов, таблиц, карт, зарисовок на доске, плоских моделей и пр.
Компьютер индивидуального пользования предполагает использование компьютерного сопровождения.
Практические методы.
Практические методы обучения основаны на
практической деятельности учащихся. Этими методами формируют
практические умения и навыки.
Упражнения. (Под упражнениями понимают повторное (многократное)
выполнение умственного или практического действия с целью овладения им
или повышения его качества.)
- Устные упражнения;
- Воспроизводящие (упражнения по воспроизведению известного с целью закрепления);
- Тренировочные (упражнения по применению знаний в новых условиях).
5.3. Методы обучения в зависимости от характера познавательной деятельности учащихся.
Объяснительно-иллюстративный.
Основное назначение метода — организация усвоения информации обучаемыми путем сообщения им учебного материала и обеспечение его успешного восприятия. Объяснительно-иллюстративный метод — один из наиболее экономных способов передачи учащимся обобщенного и систематизированного опыта. Сообщение учебной информации с использованием различных дидактических средств: слова, различных пособий.
Проблемный.
Основное назначение метода — раскрытие в изучаемом учебном материале различных проблем и показ способов их решения Выявление и классификация проблем, которые можно ставить перед учащимися, формулировка гипотез и показ способов их проверки. Учащиеся не только воспринимают, и запоминают готовые научные выводы, но и прослеживают за логикой доказательств, за движением мыслей учителя.
Частично-поисковый метод.
Основное назначение метода – постепенная подготовка обучаемых к самостоятельной постановке и решению проблем. Подведение обучаемых к постановке проблемы, показ им, как необходимо находить доказательства, делать выводы из приведенных фактов, построить план проверки фактов. Учащиеся активно участвуют в эвристических беседах, и овладевают приемами анализа учебного материала с целью постановки проблемы и нахождения путей ее решения.
5.4. Принципы организации учебной деятельности.
Учёт возрастных и индивидуальных особенностей детей.
Для слабого ученика с проблемами усвоения учебного материала необходимо:
-при работе в группе предложить доступные задания;
-предоставить возможность консультации с учителем вне урока;
-дать возможность представить свою работу в той форме, которая наиболее удобна для ученика.
Таким образом, необходимо приложить все усилия, чтобы проблемный ученик почувствовал свою значимость.
Для одарённого ученика:
-вопросы, рассматриваемые в работе, выходят за рамки школьной программы;
-в ходе работы возможны различные пути изучения материала, которые может выбрать сам ученик;
-он проводит более глубокие исследования, расширяя поле деятельности.
5.5. Формы организации учебной деятельности учащихся.
Учебный процесс предполагает органическое единство средств методов и приемов работы с организационными формами обучения. Каждому методу, приему обучения соответствует своя организационная форма, определяющаяся отношениями между учителем и учащимися и учащихся между собой.
Учитель управляет всей учебной деятельностью на уроке, используя при этом общие (работа со всем классом), групповые (пары, группы и т. д.) и индивидуальные формы ее. Указанные выше формы организации учебной деятельности выступают на уроке в различных сочетаниях и последовательностях.
В современных условиях обучения достаточно четко ставится вопрос о применении таких организационных форм работы на уроке, которые обеспечивали бы эффективное приобретение не только знаний, умений и навыков, но и ценного опыта нравственных и коллективистских отношений:
-коллективная;
-работа в группах;
-работа в парах;
самостоятельная работа.
6. Система знаний и система деятельности.
На изучение раздела «Действия с рациональными числами» в курсе математики 6 класса по программе Н.Я. Виленкина отводится на 23 часа. В ходе работы над темой в школьном курсе математики 6 класса учащиеся должны знать: определение рациональных чисел, понятие периодической дроби, свойства сложения рациональных чисел, знать правила сложения рациональных чисел; должны уметь: представлять рациональное число в виде десятичной дроби, либо в виде периодической дроби, применять свойства действий с рациональными числами при нахождении значений выражений применять предписание для сложения рациональных чисел.
| Знания | Характеристика деятельности учащихся |
| Сложение и вычитание положительных и отрицательных чисел | При изучении данной темы у учащихся отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами |
| Умножение и деление положительных и отрицательных чисел | Навыки умножения и деления положительных и отрицательных чисел учащиеся отрабатывают сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения при вычислении значений числовых выражений |
| Рациональные числа | При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. Учащиеся умеют представлять в виде десятичной дроби такие дроби, как 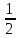 ; ; 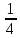 ; ; 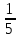 ; ; 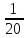 ; ; 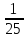 ; ; 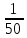 |
| Свойства действий с рациональными числами | Учащиеся должны применять законы арифметических действий для рационализации вычислений |
7. Поурочное планирование раздела программы
«Действия с рациональными числами»
| 1. Сложение и вычитание положительных и отрицательных чисел (11ч) |
| № | Тема | Кол – во часов | Цели уроков | Используемые методические средства | Формы организации учебной деятельности | Методы обучения |
| 1-2 | Сложение чисел с помощью координатной прямой | 2 | Показать учащимся, как складываются числа с помощью координатной прямой | -презентация; - тесты | -коллективная работа; -работа в группах; -самостоя тельная работа | Проблемный |
| 3-4 | Сложение отрицательных чисел | 2 | Вводится правило сложения отрицательных чисел | -презентация; -тесты; -индивидуаль ные карточки; -тренажёры для отработки действий; - дидакт. игра | -коллективная работа; -работа в группах; -самостоя тельная работа | Проблемный Частично – поисковый |
| 5-7 | Сложение чисел с разными знаками | 3 | Вводится правило сложения чисел с разными знаками | -презентация; -тесты; -индивидуаль ные карточки; -тренажёры для отработки действий; - дидакт. игра | -коллективная работа; -работа в группах; -самостоя тельная работа | Проблемный Частично — поисковый |
| 8 8-10 | Вычитание | 3 | Вводится понятие вычитания чисел | -презентация; -тесты; -тренажёры для отработки действий; -дидакт. игра. | коллективная работа; -работа в группах; -самостоя тельная работа | Проблемный Частично — поисковый |
| 11 | Контрольная работа | 1 | Контроль знаний | индивидуальные карточки |
|
|
| 2.Умножение и деление положительных и отрицательных чисел(12ч) |
|
| Тема | Кол – во часов | Цели уроков | Используемые методические средства | Формы организации учебной деятельности | Методы обучения |
| 1-3 | Умножение | 3 | Вводится правило умножения положительных и отрицательных чисел | -презентация; - тесты; -тренажёры для отработки действий; - дидакт. игра | -коллективная работа; -работа в группах; -самостоя тельная работа | Проблемный |
| 4-6 | Деление | 3 | Вводится правило деления отрицательных чисел, и чисел с разными знаками | -презентация; - тесты; -тренажёры для отработки действий | -коллективная работа; -работа в группах; -самостоя тельная работа | Проблемный |
| 7-8 | Рациональные числа | 2 | Водится понятие рациональных чисел либо в виде десятичной дроби, либо в виде периодической дроби | -презентация; -тесты; -индивидуальные карточки; | -коллективная работа; -работа в группах; -самостоя тельная работа | Объяснительно — иллюстративный |
| 9-11 | Свойства действий с рациональными числами | 3 | Повторение переместительного и сочетательного закона сложения, показать на примерах их применение для рациональных чисел | -презентация; - тесты; -тренажёры для отработки действий | -коллективная работа; -работа в группах; -самостоятельная работа | Частично — поисковый |
| 12 | Контрольная работа | 1 | Контроль знаний | -индивидуальные карточки |
|
|
8. Разработка урока по теме
«Деление положительных и отрицательных чисел»
Тип урока: урок изучения и первичного закрепления новых знаний.
Вид урока: комбинированный.
Цели урока:
Познавательная - выработать навыки деления чисел с разными знаками;
Развивающая - развитие интеллектуальных и творческих способностей учащихся, познавательной активности, интереса к изучению математики,навыков устного счета;
Воспитательная - воспитание качеств личности, формируемых в ходе учебной математической деятельности и обеспечивающих творческую активность, способность принимать самостоятельные решения, воспитание самоконтроля и взаимоконтроля учащихся.
Оборудование и материалы: компьютер, мультимедийный проектор, экран мультимедийная презентация.
Этапы и их продолжительность:
Организационный момент 2 мин.
Сообщение целей и темы урока 2 мин.
Актуализация опорных знаний 10 мин.
Изучение нового материала 3 мин.
Закрепление нового материала 5 мин.
Физкультминутка 2 мин.
Решение примеров 17 мин.
Задание на дом 2 мин.
Подведение итогов урока, выставление оценок 2 мин.
Система знаний и система деятельности учителя и учащихся:
| Этап урока | Деятельность учителя | Деятельность ученика |
|
| Организационный момент | Приветствует, определяет готовность, комплектует группы; объясняет цель создания групп. | Отвечают на приветствие, рассаживаются в группы. |
| Сообщение целей и темы урока | -Мы продолжаем изучать действия с положительными и отрицательными числами. Какие действия с этими числами вы умеете выполнять?
Какое действие вы еще не умеете выполнять? Значит, чем сегодня на уроке нам предстоит заниматься?
Сегодня мы изучим правила деления положительных и отрицательных чисел (слайд 1). | Вспоминают правила сравнения, сложения, вычитания и умножения положительных и отрицательных чисел. - Деление.
Делают вывод, чем сегодня на уроке предстоит заниматься.
Открывают тетради и записывают тему урока. |
| Актуализация опорных знаний | -Прежде, чем изучить новый материал, обратимся к истории математики.
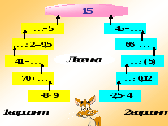
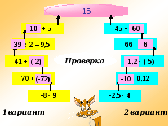
Организует деятельность по актуализации правил действий с положительными и отрицательными числами. - Повторим пройденный материал. 1 задание: сравнить значения выражения (слайды 2,3), затем проверяют решения (ответы появляются на экране); 2 задание: Лесенка Класс делится на две группы. Каждая группа решает свой вариант. Затем проверяются решения (ответы появляются на экране щелчком мыши) (слайды 4, 5, 6).. | Слушают сообщение Митрофанова Олега об истории создания отрицательных чисел.
Сравнивают выражения, объясняя используемые правила. Работают в группах. Каждая группа выполняет действия, затем проверяют правильность решений |
| Изучение нового материала | Организует работу по изучению новой темы. -Сегодня мы начинаем изучать последнее арифметическое действие – деление. Объяснение темы: a:b=x Как найти делимое?
- Как найти делимое в данном выражении? -15:5=х (слайд 7)
Определите знак частного.
Записывает на доске: (-) : (+) = (-)
Как вы думаете, если разделить положительное число на отрицательное, число с каким знаком получится? Записывает на доске: (+) : (-) = (-) Какой можно сделать вывод?
- Как найти делимое в данном выражении? -15: (-5)=х
Какой знак получится при делении двух отрицательных чисел?
Записывает на доске (-) : (-) = (+) Итак, какие правила деления вы сегодня узнали?
(слайд 8)
|
Формулируют правило нахождения делимого. Чтобы найти делимое нужно частное умножить на делитель. Один из учеников записывает на доске как найти делимое x•b=a
Объясняют решение. Один из учеников записывает на доске как найти делимое х•5=-15 х=-3. Остальные записывают пример в тетрадь.
Формулируют правило деления отрицательного числа на положительное: при делении отрицательного числа на положительное получится отрицательное число.
Объясняют результат.
Проговаривают правило деления чисел с разными знаками.
Объясняют, как найти делимое: х (-5)=-15 (-5)=-15 х=3 Проговаривают правило деления двух отрицательных чисел.
Формулируют правила деления положительных и отрицательных чисел. |
| Закрепление нового материала | Организует работу по закреплению новой темы. Устный счет. 1). Солнышко (слайд 9). (Ответы – последовательно щелчком мышки по пустому полю слайда) 2). Решение примеров (слайд 10). Для проверки примеров используется триггер, что позволяет начать проверку с любого примера. При нажатии на пример появляется ответ.
| Выполняют устно деление, проверяют ответы.
Решают самостоятельно примеры, сравнивают ответы. Исправляют неправильные ответы (если есть), объясняя ошибки. |
| Физкультминутка | Организует работу снятию усталости. -Сейчас немного отдохнем: Все умеем мы считать Раз, два, три, четыре, пять — Все умеем мы считать. Раз! Подняться потянуться. (Под счет учителя дети выполняют потягивания.) Два! Согнуться, разогнуться. (Наклоны. Повороты туловища.) Три! В ладоши три хлопка, Головою три кивка. (Движения головой.) На четыре - руки шире. (Хлопки в ладоши.) Пять — руками помахать. (Движения руками.) Шесть — за парту тихо сесть. (Прыжки. Ходьба на месте.)
| Один из учащихся показывает движения. Остальные встают, выполняют упражнения. |
| Решение примеров | Организует работу с учебником. Решаем примеры из учебника № 1152(а,б,в).
Организует самостоятельную работу.
Решите уравнения самостоятельно (слайд 11), ответы появляются на экране.
Решаем кросснамбер. Класс делится на 2 группы. Каждой группе выдается листок с кросснамбером.
Контролирует ход решения примеров и взаимооценки решений.
Проводит оценивание по решению кросснамбера.
|
Три ученика выходят к доске, решают примеры, по очереди проговаривая решения, остальные решают на месте, сверяя ответы на доске.
Решают самостоятельно уравнения, сравнивают ответы.
Работают в группах по карточке. Решают примеры, вписывают ответы в клетки кросснамбера. Затем обмениваются листочками и проверяют ответы другой группы. |
| Задание на дом | Запишите домашнее задание: № 1152 (г, д, е), № 1156. | Записывают домашнее задание в дневники. |
| Подведение итогов урока, выставление оценок | Подводит итоги урока (рефлексия). - Итак, сегодня мы изучили правила деления положительных и отрицательных чисел. Вспомните эти правила (возврат к слайду 8).
Ответьте на вопросы: Что полезного надо запомнить?
Сегодня на уроке я повторил...
Сегодня на уроке у меня получилось…
Объявляет оценки за урок. Итак, друзья, урок мы провели, Все сделали мы с вами, что смогли. Желаю к математике вам прилагать старанье. Всего вам доброго, друзья, и до свиданья! |
Проговаривают правила деления.
Подводят итоги урока. - Знаки при делении положительных и отрицательных чисел.
- Правила сравнения, сложения, вычитания и умножения положительных и отрицательных чисел.
- Выполнять деление, правильно определять знаки и т.п. |
Список литературы.
Жохов В.И. Математический тренажер. 6 класс. – М.: Мнемозина, 2012;
Иванова Т.А. Современный урок математики: теория, технология, практика: книга для учителя. – Н. Новгород: НГПУ, 2010;
Игнатьева Г.А., Волкова В.О., Шишкина О.П. – Дидактика развивающего обучения : - Н.Новгород, 1998;
Картанова М.Н. Уроки математики с применением ИКТ. 5 – 6 классы. – М.: Планета, 2010;
Каплунович И.Я., Петухова Т.А. Пять подструктур математического мышления: как их выявить и использовать в преподавании. // Математика в школе. – 1998. - № 5
Клепиков В.Н. О формировании мировоззрения школьников средствами математики. // Математика в школе, 2008. - № 9;
Крымова Л.Н. Интерактивная доска на уроках математики. – Математика в школе, 2008. - № 10;
Панишева О.В. Математика в стихах : задачи, сказки, рифмованные правила. 5 – 11 классы – Волгоград: Учитель,2013;
Пичурина Г.Б. Индивидуальные особенности мышления учащихся в процессе преподавания математики. // Педагогическое обозрение, 2008. - № 1;
Селевко Г.К. Современные образовательные технологии: учебное пособие. – М.: Народное образование, 1998.
Интернет – ресурсы
www.alleng.ru
www.kabmetodist.ru
www.nsportal.ru
www.zauch.info
www.pedsovet.su
Приложение 1.
Анализ урока
1. Пояснительная записка.
Урок «Деление положительных и отрицательных чисел» проводился в 6 классе Исуповской СОШ в 2012 – 2013 уч. году.
Цели урока:
Познавательная - выработать навыки деления чисел с разными знаками;
Развивающая - развитие интеллектуальных и творческих способностей учащихся, познавательной активности, интереса к изучению математики,навыков устного счета;
Воспитательная - воспитание качеств личности, формируемых в ходе учебной математической деятельности и обеспечивающих творческую активность, способность принимать самостоятельные решения, воспитание самоконтроля и взаимоконтроля учащихся.
Тип урока: урок изучения и первичного закрепления новых знаний.
Вид урока: комбинированный.
Количество часов – 1.
Работа на уроке проходила с использованием электронной презентации, демонстрация которой проходила на экране.
Место урока в структуре образовательного процесса – урок по учебному плану в 6 классе по теме «Натуральные числа».
Учебник: «Математика 6». Н.Я.Виленкин, В.И.Жохов и другие.
По программе Жохова В.И. «Планирование учебного материала. Математика 5 – 6 классы» на изучение темы «Деление положительных и отрицательных чисел» отводится 3 часа. Урок, который я представляю, первый из них.
Характеристика класса.
В 6 классе, в котором проходил урок, 7 учащихся. Все они отличники. Класс очень активный. Дети очень любознательные, старательные. На уроках выполняют все задания, любят интересные, нестандартные задачи. Группы я создавала, учитывая доминантные подструктуры мышления учеников (по теории И. Я. Каплуновича). В каждой группе есть учащиеся с топологической подструктурой мышления (Полякова М., Малафеев А.), алгебраической (композиционной) подструктурой (Полякова П., Волков А., Митрофанов О.). В команде девочек есть ученица с доминантной порядковой подструктурой (Кузнецова Е.), в команде мальчиков – с метрической подструктурой мышления (Гладышев С.). Ученики с топологической подструктурой мышления не любят торопиться, все делают скрупулезно, все проверяют, чтобы не пропустить ни одной ошибки. Для учащихся с порядковой подструктурой работа по правилу, алгоритму, образцу является любимым занятием. Дети с метрической подструктурой мышления испытывают дискомфорт, если их принуждают к решению в общем виде, к поиску принципа. Ученики с алгебраической подструктурой быстро думают и действуют, усваивают новый материал, свободно устанавливают связи между фактами, но они слишком торопливы и могут допускать элементарные ошибки. Разделение по подструктурам мышления я использовала для того, чтобы в командах происходил обмен мнениями, поиск неодинаковых и многоплановых решений.
Итоги урока.
Деление на группы в этом классе я проводила не в первый раз. При работе в командах учение из индивидуальной работы каждого ученика превращается в совместный труд. Ученик становится заинтересованным в поддержании дружеских взаимоотношений.
Игровая форма урока позволила ученикам получить удовольствие не только от результата, но и от самого характера деятельности: эмоционального, поискового, состязательного, раскрепощенного.
Урок прошел в хорошем темпе. Ученики быстро справлялись с заданиями. Затруднения вызвали выражения № 1152(а,б). Они путались в знаках при вычитании отрицательного числа. Это типичная ошибка многих учеников не только этого класса. При решении кросснамбера затруднение вызвало неравенство с модулем. Поэтому на следующем уроке необходимо повторить решение неравенств с модулем. В остальных заданиях ошибок не допускали. Все цели урока были достигнуты.
Материалы к уроку.
Слайды 2, 3


Слайды 5, 6.
Слайды 7, 8.
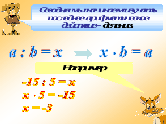
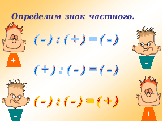
Слайд 9.
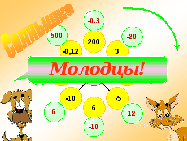
Слайды 10, 11.
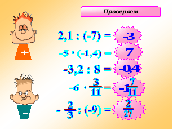

Кросснамбер.
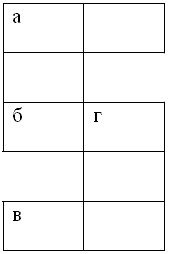
По горизонтали:
а) Вычислить: - 12,9 + 8,14 – 3,1+ 40,86;
б) Вычислить: - 81 ∙ (- 1);
в) Вычислить: (- 5,5 + 55) + ( - 6,5).
По вертикали:
а) Вычислить: - 2,5 ∙ (-104) + (- 104) : (-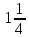 );
);
г) Количество целых чисел, удовлетворяющих неравенству: │х │
Доклад «История отрицательных чисел»
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или, как у Диофанта, признавались как временные значения. Умножение и деление для отрицательных чисел тогда ещё не были определены. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными.
В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Даже в XVII веке Паскаль считал, что 0-4=0, так как ничто не может быть меньше, чем ничто. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей).
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Приложение 2.
Результаты контрольных работ по теме
«Действия с рациональными числами» в 6 классах
| Контрольная работа «Сложение и вычитание положительных и отрицательных чисел» | 2010-2011 уч.г. | 2011-2012 уч.г. | 2012-2013 уч.г. |
| Количество учащихся в классе | 1 | 2 | 7 |
| Количество выполнявших работу | 1 | 2 | 7 |
| % выполнения | 100% | 100% | 100% |
| На «4» и «5» (%) | 100% | 50% | 100% |
|
|
| Контрольная работа «Свойства действий с рациональными числами» | 2010-2011 уч.г. | 2011-2012 уч.г. | 2012-2013 уч.г. |
| Количество учащихся в классе | 1 | 2 | 7 |
| Количество выполнявших работу | 1 | 2 | 7 |
| % выполнения | 100% | 100% | 100% |
| На «4» и «5» (%) | 100% | 50% | 100% |
Задания для устного счета
Выберите правильный ответ
|
| а | б | в | г |
| -17  5 5 | 85 | -85 | 75 | -75 |
| 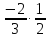
| 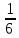
| 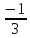
| 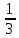
| 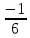
|
|  ( (
| 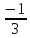
| 
| 
| 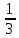
|
|  2 2
| 
| 
| 
| 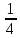
|
Математический диктант
Ответы – последовательно щелчком мышки по пустому полю слайда. Управляющая кнопка «Печать» - переход на текстовый документ для печати заданий математического диктанта.
Заполните пропуски.
При проверке используется триггер. Нажать на любой пример, и появится ответ.
Карточки
1.Вписать в квадрат такие числа, чтобы суммы их в каждой строке, столбце и диагонали были равными.
|
| 8 |
| - 14 |
| 2 |
| -8 | -4 |
| 6 | - 2 |
|
|
| 4 |
| - 18 |
|
3.По образцу найти значение выражения:
Образец:
а) 0,84 ∙ 6 + 0,16 ∙ 6 =
б) 0,77 ∙ 23 + 0,77 ∙ 77 =
в) 
г)







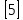 .
. 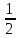 ;
; 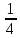 ;
; 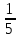 ;
; 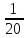 ;
; 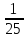 ;
; 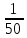
 (-5)=-15
(-5)=-15



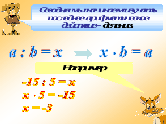
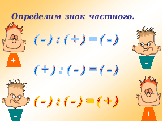

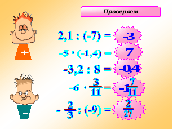


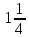 );
);