Всероссийский конкурс «Учитель года»
Муниципальный этап
Конкурсное задание
«Методическое портфолио»
Тема: «Применение активных форм и методов обучения
на уроках математики»
Молчанова Елена Викторовна, учитель математики
МКОУ Валентиновская основная общеобразовательная школа Кантемировского муниципального района Воронежской области
Важными задачами современного образования являются всестороннее развитие личности ребенка, его творческих возможностей, сохранение физического и психического здоровья. В общем объёме знаний, умений и навыков, получаемых учащимися в школе, важное место принадлежит математике, которая широко применяется при изучении других предметов и в практической деятельности, например, в овладении новой техникой, которая благодаря своему стремительному развитию все прочнее входит в нашу жизнь, в понимании результатов статистических исследований. Математика является инструментом познания мира, помогает осознать его законы, понимать логику происходящих событий. В современной школе нагрузка на учащихся школ высока. Однако проблему загруженности учащихся можно решать также и применением активных методов и форм обучения, ведь усталость по большей части – психологическая проблема. Если ученик заинтересован, вовлечен, активен, то он не чувствует усталости. А ведь помимо этого, активные методы и формы обучения эффективны еще и с точки зрения усвоения материала.
Активные методы и формы обучения - методы, стимулирующие познавательную деятельность обучающихся. Активные методы обучения строятся на практической направленности, игровом действе и творческом характере обучения, интерактивности, разнообразных коммуникациях, использовании знаний и опыта обучающихся, групповой форме организации их работы, вовлечении в процесс всех органов чувств, деятельностном подходе к обучению, движении и рефлексии. Эффективность процесса и результатов обучения с использованием активных методов обучения определяется тем, что разработка методов основывается на серьезной психологической и методологической базе. Для каждого этапа урока используются свои активные методы, позволяющие эффективно решать конкретные задачи этапа.
Активные формы обучения в преподавании математики:
Дидактические игры — это вид учебных занятий, организуемых в виде учебных игр, реализующих ряд принципов игрового, активного обучения и отличающихся наличием правил, фиксированной структуры игровой деятельности и системы оценивания, один из методов активного обучения. Наиболее целесообразно использовать дидактические игры и игровые ситуации при проверке результатов обучения, выработке навыков, формировании умений.
Дидактическая игра «Юный художник».
Эта игра проводится по теме «Координатная плоскость». Ученикам предлагается отметить точки на координатной плоскости, которые нужно в той же последовательности соединить отрезками, в результате которых получается определенный рисунок. А также предлагается обратное задание: нарисовать любой рисунок, имеющий конфигурацию ломанной, и записать координаты вершин.
Игра «Горячий стул» - ученик садится на стул, а учащиеся задают примеры для устного решения до тех пор, пока он не собьется, затем его сменяет тот, кто предложил последний пример, игра продолжается. Побеждает тот, кто решил больше примеров.
Игра «Считайте, не зевайте» - каждый член команды получает табличку, на которой написаны номера от нуля до девяти. Учитель зачитывает задание, ребята устно считают, обладатели табличек с цифрами, из которых образуется ответ, должны выбежать к доске и вставить так, чтобы получился правильный ответ. Например, задание: уменьшить сумму чисел 49 и 47 в 8 раз, обладатели номеров 1 и 2 выбегают и встают, чтобы получилось 12.
Игру «математическое домино» целесообразно проводить по теме «Действия с обыкновенными дробями», «Действия с рациональными числами. Игра проводится:
1) в начале урока, разделив класс по рядам, с целью включить учащихся в работу на уроке;
2) как дополнительное задание для детей решающих быстрее остальных, разделив их на пары;
3) как дополнительные занятия после уроков.
На уроках геометрии можно предложить игру «Теорема - пазл». Учащимся предлагается собрать теорему из 4 фрагментов. На одном содержится формулировка теорем, на другом – чертеж к теореме, на третьем - что дано и что требуется доказать, на четвертом - доказательство.
В качестве закрепления нового материала успешно применяется игра «Верю - Не верю». Например, на уроке математики в 6 классе по теме «Рациональные числа» можно использовать такие вопросы:
-25- число отрицательное? (да)
89- число положительное?(да)
При сложении отрицательных чисел получается число положительное (нет)
-3+(-5) = 8 (нет)
-15 +(-26)= -41 (да)
Нуль больше любого отрицательного числа (да)
Из двух отрицательных чисел то больше, модуль которого больше (нет)
Из двух чисел то число больше, которое находится правее на координатной прямой (да)
Чтобы выявить, насколько хорошо усвоена та или иная тема по математике, применяются различные формы контроля знаний. Одна из них - тесты.
Тестовые задания удобно использовать при организации самостоятельной работы учащихся в режиме самоконтроля, при повторении учебного материала.
Тесты обеспечивают возможность объективной оценки знаний и умений учащихся в балах по единым критериям. Это позволяет определить, кто овладел им на минимальном уровне, кто уверенно владеет знаниями и умениями на более высоком уровне, чем это предусмотрено программой. Задание должно обеспечивать проверку знаний и умений на трех уровнях: узнаваемости и воспроизведения, применения в знакомой ситуации или творческого применения.
Например, урок математики в 5 классе на тему «Обыкновенные дроби»,
«Закончи фразу!».
Обыкновенная дробь состоит из ...
2. При сравнении дробей с одинаковыми знаменателями сравнивают ...
3. На координатной прямой меньшая дробь расположена ...
4. Дробь, в которой числитель меньше знаменателя называется ...
5. Знаменатель дроби показывает ...
Метод ассоциации.
Гораздо легче усваивается ход решения, если некоторые его моменты связаны с жизнью, этапы решения сравниваются с понятиями окружающего мира. В этом случае математическое умозаключение ассоциируется с представлениями реальной действительности, либо происходит зрительная ассоциация.
При переносе слагаемых из одной части уравнения в другую, ребята очень часто допускают ошибку, забывая менять знаки на противоположные. Можно предложить им под знаком «=» подразумевать границу нашей страны, чтобы поехать за границу нам обязательно надо поменять российский паспорт на заграничный. И решая уравнения, нужно внимательно определить «едет» ли данное слагаемое за границу (нужно поменять знак на противоположный) или только поменяло место жительства в стране ( оставляем с тем же знаком).
При решении систем неравенств, обращая внимание на двойную штриховку, прошу записать ответ промежуток, где «выросла елка».
Изучая неравенства, ребята часто путают знаки и или . Тогда легко убедиться, что стрелка показывает направление штриховки на оси.
Метод самоконтроля, самоанализа, самооценки полученных знаний на уроке.
В течение урока ученики поэтапно заполняют маршрутные листы или листы успеха или индивидуальные карточки контроля знаний. За каждый этап учащийся в течение всего урока самостоятельно выставляет набранное количество баллов, в конце урока суммирует баллы и выставит себе оценку за урок.
Методы получения обратной связи. «Незаконченное предложение».
Участникам предлагается закончить следующие предложения:
Самый главный вопрос, который был поставлен сегодня…
Самым трудным для меня на сегодняшнем занятии было…
3. Сегодня я понял(а), что…
Новые педагогические технологии немыслимы без широкого применения ИКТ (информационно-коммуникационных технологий), именно они позволят в полной мере раскрыть педагогические, дидактические функции этих методов, реализовать заложенные в них потенциальные возможности.
Известно, что ученики проявляют большой интерес, когда при объяснении нового материала применяются презентации. Даже самые пассивные из них с огромным желанием включаются в работу, с интересом просматривают слайды и отвечают на вопросы. Поэтому я использую презентации в программе Microsoft Power Point, как изложение к объяснительному материалу, закрепление изученных тем, знакомство с историей математики, как иллюстрации внеклассных мероприятий.
Остановлюсь подробнее на применении приемов технологии Критического мышления на своих уроках.
Приём «Синквейн» - это стихотворение, представляющее собой синтез информации в лаконичной форме, что позволяет описывать суть понятия или осуществлять рефлексию на основе полученных знаний. Для его написания существуют следующие правила:
Название – 1 существительное, описание – 2 прилагательных, действия – 3 глагола, чувство – фраза из 4 слов, повторение сути – синоним (1 слово)
Примеры синквейнов, составленных учениками:
Треугольник
Равнобедренный, равносторонний
Строится, является, называется
Сумма сторон треугольника – периметр
Фигура
Прием "Кластеры" используется как на стадии вызова, так и на стадии рефлексии, т.е. может быть способом мотивации к размышлению до изучения темы или формой систематизирования информации при подведении итогов.
В зависимости от цели организуется индивидуальная или самостоятельная работа учащихся или коллективная – в виде общего совместного обсуждения.
Например, составление кластера по теме «Квадратные уравнения»
Квадратные уравнения
ax2 + bx + c = 0, где a 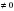
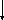
 Неполные квадратные уравнения
Неполные квадратные уравнения
ax2 + bx = 0 ax2 + c = 0 ax2 = 0
x (ax + b) = 0 ax2 = -c x2 = 0
x = 0 или ax +b = 0 x2 = - 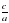 x = 0
x = 0
x = - 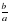 Если
Если 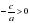 , то
, то
x1= 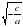
x2= -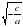
 Приведенное квадратное уравнение
Приведенное квадратное уравнение
x2 + px + q = 0
Практика показывает, что активные методы и формы обучения - очень мощный инструмент в руках учителя. Методически верно организованные они требуют от учащихся активной познавательной деятельности не только на уровне воспроизведения или преобразования, но и на уровне творческого поиска, способствуют сотрудничеству учителя и учащихся в процессе обучения.
Без хорошо продуманных методов обучения трудно организовать усвоение программного материала. Вот почему следует совершенствовать те методы и средства обучения, которые помогают вовлечь учащихся в познавательный поиск, в труд учения: помогают научить учащихся активно, самостоятельно добывать знания, возбуждают их мысль и развивают интерес к предмету.
При системном внедрении активных методов я рассчитываю, через мотивацию и интерес повысить качество знаний предмета математика. В своей будущей педагогической деятельности мне необходимо продолжить целенаправленную работу по развитию способных учеников, чтобы они проявили талантливость и одаренность.
И закончить хочу словами И.Г.Песталоцци
«Мои ученики будут узнавать новое не от меня;
они будут открывать это новое сами.
Моя главная задача - помочь им раскрыться,
развить собственные идеи».







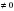
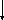
 Неполные квадратные уравнения
Неполные квадратные уравнения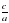
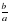 Если
Если 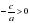 , то
, то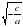
 Приведенное квадратное уравнение
Приведенное квадратное уравнение



















