Множества. Понятие и операции над ними.

Множества

Попова И.В.,

учитель математики

МАОУ гимназия №1

г. Калининград

Разминка

1. Назовите общие буквы в словах:

а) часы, мыло;

б) корова, вафля;

в) лошадь, шалость;

г) стол, стул;

д) клоп, полк;

е) вилка, ложка, бутылка.

Разминка

2. Назовите общие цифры у чисел:

а) 1255, б) 39

3842 13809

в) 8412, г) 387

1428 401

Определение

• Одним из фундаментальных, неопределяемых математических понятий является понятие множества.
• Множество можно представить себе как соединение, совокупность, собрание некоторых предметов, объединенных по какому-либо признаку:

• множество учащихся класса,
• множество букв алфавита,
• множество натуральных чисел,
• множество точек на прямой,
• множество книг на полке и т.д..

• Обозначают множества заглавными буквами латинского алфавита или символически с помощью фигурных скобок, в которых указываются его элементы.
• Сами элементы некоторого множества будем обозначать малыми латинскими буквами, если они не имеют специальных обозначений:
• А; {а, b, c}; {∗,s,h,g}; N={1,2,3,4,5,6,7,8, …}.

• Множества, состоящие из одних и тех же элементов называют равными (одинаковыми). Пишут А = В .
• Множество, которое не содержит ни одного элемента, называется пустым и обозначается символом ∅ .

Операции над множествами

Над множествами, как и над числами, производят операции. Рассмотрим некоторые из них:

• пересечение,
• объединение,
• разность.

Пересечение

Возьмем множество X = {а,б,в,г,д} и

множествоY = {г,д,е,ж} .

Эти множества имеют общие элементы {г,д },

поэтому множества X и Yназывают пересекающимися множествами.

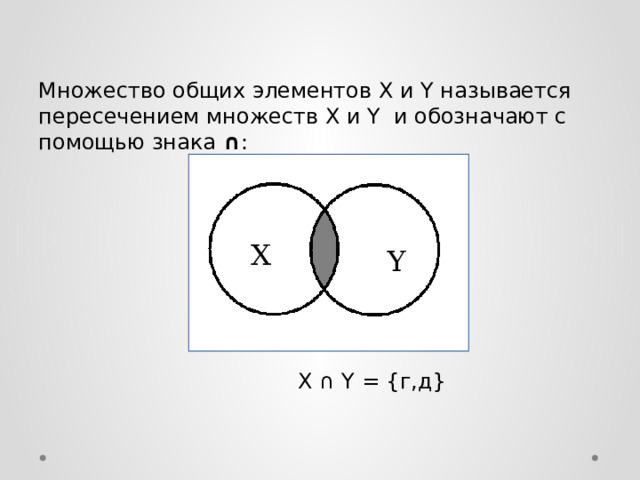
Множество общих элементов X и Y называется пересечением множеств X и Y и обозначают с помощью знака ∩ :

X ∩ Y = {г,д}

X

Y

Рассмотрим множество X = {а,б,в,г,д} и множество А = {1; 3; 5}.

Эти множества не имеют общих элементов.

В этом случае множества А и X называются непересекающимися . Пересечением множеств А и X является пустое множество:

A

X

X ∩ А = ∅ .

Объединение

Если из элементов множеств X = {а,б,в,г,д} и

Y = {г,д,е,ж} составить новое множество, состоящее из всех элементов этих множеств и не содержащее других элементов, то получится объединение множеств X и Y, которое обозначается с помощью знака  :

X  Y = {а,б,в,г,д,е,ж}

X

Y

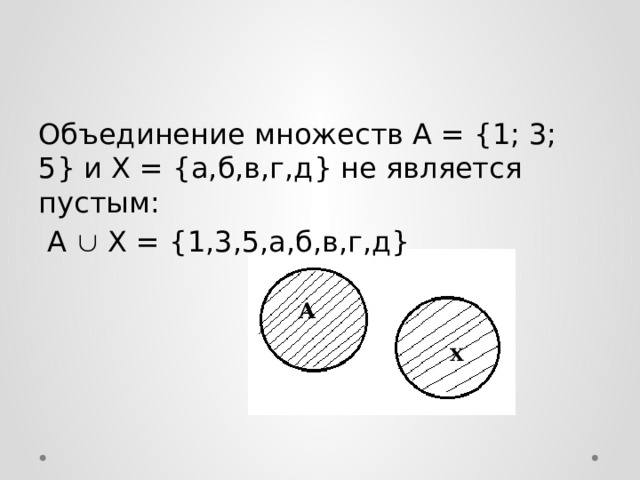
Объединение множеств А = {1; 3; 5} и X = {а,б,в,г,д} не является пустым:

A  X = {1,3,5,а,б,в,г,д}

A

X

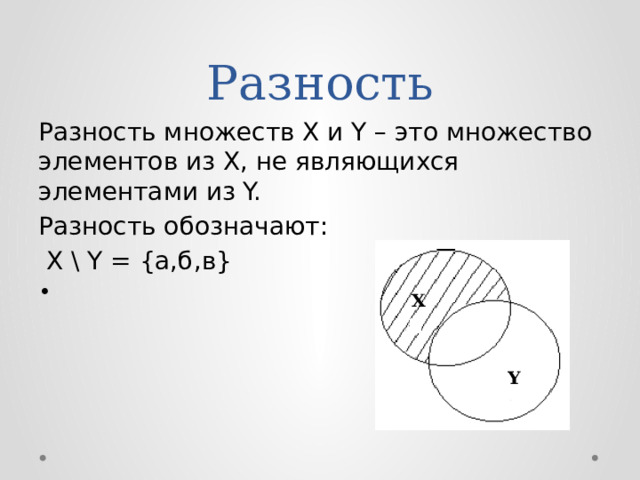
Разность

Разность множеств X и Y – это множество элементов из X, не являющихся элементами из Y.

Разность обозначают:

X \ Y = {а,б,в}

X

Y

Разность между множеством и его подмножеством называют дополнением .

Пусть множество B={3,5} является подмножеством A = {1,3,5}. Множество элементов А, которые не вошли в В, называют дополнением до А. И обозначают = {1}.

A

B

= A \ B

Практическая часть

№ 1 . Даны множества

A = {1;3;5;15}, B = {1;2;3;6}.

• Подчеркните общие элементы множеств А и В;
• Запишите множество С, состоящее из общих элементов А и В.
• Запишите с помощью символов фразу «пересечением множеств А и В является множество С».

Практическая часть

№ 2. Найдите пересечение множеств А и В,

если А = {2; 4; 6; 8; 10; 12},

B = {3; 6; 9; 12}.

Практическая часть

№ 3 . Заполните пропуски так, чтобы получилось верное равенство:

а) {1; 2; 3} ∩ {2; 3; _ } = {2; 3};

б) {1; 2; 3} ∩ { _ ; _ ; _ } = ∅;

в) {1; 2; 3} ∩ { _ ; _ ; _ } = {1; 2; 3};

г) {1; 2; 3} ∩ { _ ; _ ; _ ; _} = {1; 2; 3}.

Практическая часть

№ 4 . Заполните пропуски так, чтобы получилось верное равенство:

а) А ∩ В = В ∩ _ ;

б) А ∩ ∅ = _ ;

в) А ∩ А = _ .

Практическая часть

№ 5 . Запишите с помощью символов фразу «объединением множеств M и P является множество Т».

Практическая часть

№ 6 . Найдите объединение множеств А и В,

если А = {3; 6; 9; 12},

В = {2; 4; 6; 10; 12}.

Подсказка: выпишите сначала все элементы множества А, а потом дополните элементами из множества В, которые еще не записали.

Практическая часть

№ 7 . Заполните пропуски так, чтобы получилось верное равенство:

а) {1; 2; 3; 4}  { _ ; _ ; _ } = { _ ; _ ; _ ; _ ; _ ; _ ; _ };

б) {1; 2; 3; 4}  { _ ; _ ; _ } = { _ ; _ ; _ ; _ ; _};

в) {1; 2; 3; 4}  { _ ; _ ; _ } = { _ ; _ ; _ ; _ };

г) {1; 2; 3; 4}  { _ ; _ ; _ } = { _ ; _ ; _ ; _ ; _ ; _ }.

Практическая часть

№ 8 . Заполните пропуски так, чтобы получилось верное равенство:

а) А  В = В  _ ;

б) А  ∅ = _ ;

в) А  А = _ .

Практическая часть

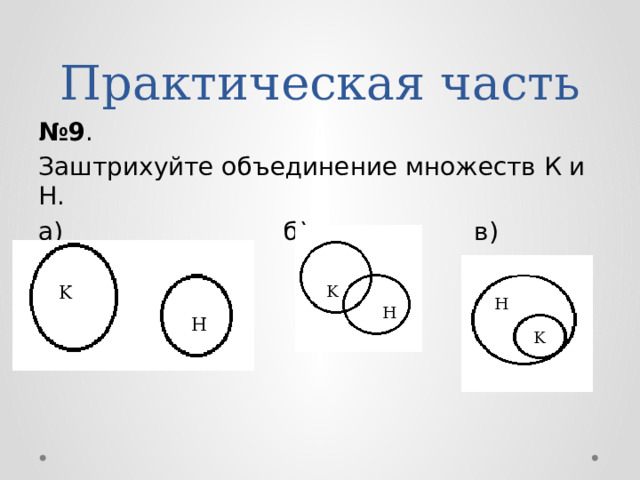
№ 9 .

Заштрихуйте объединение множеств К и H.

а) б) в)

K

K

H

H

H

K

Практическая часть

№ 10 .

Заштрихуйте вертикальной штриховкой объединение, а горизонтальной пересечение множеств Р и Q.

P

Q

Практическая часть

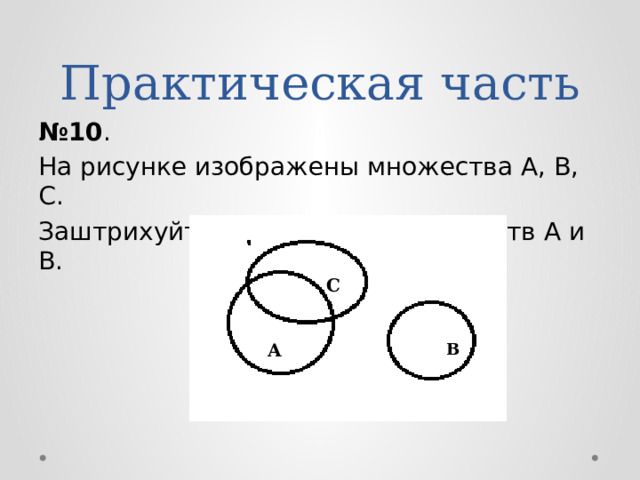
№ 10 .

На рисунке изображены множества А, В, С.

Заштрихуйте объединение множеств А и В.

С

А

В

Практическая часть

№ 10 .

Даны множества:

М = {5, 4, 6},

Р = {4, 5, 6},

Т = {5, 6, 7},

S = {4, 6}.

Какое из утверждений неверно?

а) М = Р б) Р ≠ S в) М ≠ Т г) Р = Т

Спасибо за внимание!