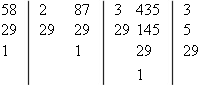Наименьшее общее кратное

Наименьшее общее кратное

Цели урока:

1. Обучающая:

• дать определение наименьшего общего кратного, показать способы нахождения НОК;

• сформировать способность к использованию выведенного алгоритма для решения задач;

• отработать навыки нахождения наименьшего общего кратного;

• повторить и закрепить понятие простого и составного числа, разложение чисел на простые множители.

2. Развивающая:

• продолжить формирование ряда умений частично-поисковой познавательной деятельности: осознать проблему, делать выводы и обобщения.

2. Воспитательная:

• пробудить у учащихся интерес к учебному материалу и познавательным действиям;

• формировать умения, аккуратность, грамотность математической речи.

Ход урока

1 этап. Организационный момент. Проверка домашнего задания.

2 этап. Работа устно.

1. Какие числа называются простыми? Какие числа называются составными?

2. Назовите делители числа 6, 8, 17. Какие из них являются простыми делителями?

Да-Нет

1.  1 является простым число                                                                 НЕТ

2. У простого числа только два делителя: 1 и само число                   ДА

3. Наименьшим простым числом является 2                                         ДА

4. У составных чисел больше двух делителей                                       ДА

5. Наименьшим двузначным простым числом является 10                  НЕТ

6. Все простые числа нечетные                                                              НЕТ

7. Все четные числа делятся на 2                                                           ДА

8. Все нечетные числа делятся на 5                                                        НЕТ

9. Сумма двух четных чисел является четным числом                         ДА

10. Если число оканчивается цифрой 3, то оно всегда делится  на 3   НЕТ

11. Если число делится на 9, то оно всегда делится и на 3                   ДА

12.  Если число кратно 3, то сумма цифр может быть равна  34         НЕТ

3 этап. Объяснение нового материала.

- Назовите, пожалуйста, числа делящиеся на 12.

12, 24, 36, 48, 60, 72, 84, 96, 108 и т.д.

- Сколько их можно назвать?

Такие числа называются кратными числу 12 т е. числа делящиеся на 12.

- Назовите, пожалуйста, числа, кратные 18.

18, 36, 54, 72, 90, 108, 126 и т.д.

Мы видим, что имеются числа, кратные одновременно 12 и 18. Например 36, 72, 108 и т.д. Эти числа называются общими кратными чисел 12 и 18.

- Какое из них является наименьшим?

Итак, наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, делящееся нацело на каждое из чисел a и b. Это обозначают так НОК (a, b).

Наименьшее общее кратное двух чисел обычно находят одним из двух способов. Рассмотрим их.

Найдем НОК (24, 18).

I способ. Будем выписывать числа, кратные 24 (большему из данных чисел), проверяя, делится ли каждое из них на 18:

24 × 1 = 24 – не делится на 18,
24 × 2 = 48 – не делится на 18,
24 × 3 = 72 – делится на 18, поэтому НОК (24, 18) = 72.

II способ. Разложим числа 24 и 18 на простые множители:

24 = 23 × 3, 18 = 2 × 32.

НОК (24, 18) должно делиться и на 24 и на 18. Поэтому искомое число содержит все простые делители большего числа 24 (т.е. числа 2, 2, 2, 3) и ещё множители из разложения меньшего числа 18, которых нет в разложении числа большего 24 (т.е. ещё одно число 3). Поэтому НОК (24, 18) = 23 × 32 = 72.

Итак, сформулируем правило с помощью которого можно находить НОК нескольких чисел:

1. Разложить числа на простые множители.

2. Выписать разложения одного из них

3. Добавить недостающие множители из разложения оставшихся чисел

4. Найти произведение (если нужно).

4 этап. Закрепление материала.

1. Найдите НОК (360, 1020).

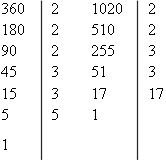
НОК (360,1020) = 23 × 32 × 5 × 17 = 6120

2. Найдите НОК (58, 87, 435).

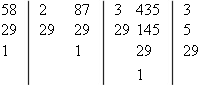
НОК (58, 87, 435) = 2 × 29 × 3 × 5 = 870

3. Найдите НОК (24, 25). Заметим, что числа 24 и 25 являются взаимно простыми т.е. общих простых делителей они не имеют. Следовательно, их наименьшее общее кратное равно произведению этих чисел.

Найдите НОК (24, 25) = 600

4. Найдите НОК (120, 24). Заметим, что 120 делится на 24, значит наименьшее кратное этих чисел равно большему из них т.е. НОК (120, 24) = 120.

6. Решим задачу №685. Из двух сцеплённых шестерёнок одна имеет 16 зубцов, а другая – 28 зубцов. До начала вращения шестерёнок соприкасающиеся зубцы пометили мелом. Через какое наименьшее число оборотов каждой шестерёнки метки будут совпадать?

Решение. Так как НОК (16, 28) = 112, то первая шестерёнка должна сделать 112 / 6 = 7 оборотов, а вторая шестерёнка – 112 / 28 = 4 оборота.
Ответ: 7 оборотов и 4 оборота.

5 этап. Итоги урока.

Мы познакомились с правилом нахождения наименьшего общего кратного нескольких натуральных чисел, использовали его при решении задач. А теперь ответьте, пожалуйста, на вопросы на вопросы:

1. Что такое НОК?

2. Какими способами можно найти НОК?

3. Какие это способы?

4. Известно, что НОК (а, в) = 18. Найдите несколько возможных ситуаций для а и в.

6 этап. Домашнее задание.

Тема урока НОК

Цель урока: учиться уверенно находить НОК чисел; решать примеры и задачи, связанные с нахождением НОК чисел.

Образовательные: отработка навыков нахождения НОК и умение решать задачи на использования НОК чисел;

Развивающие: развивать познавательный интерес к предмету; наблюдательность, внимание; формировать сознательное восприятия учебного материала.

Воспитательные: воспитывать у учащихся культуру труда, взаимоуважение, стремление хорошо учиться.

Ход урока

1. Орг момент

2. Актуализация знаний

3. Устный счёт

1. Может ли разложение на простые множители число 24753 содержать множитель 5? Почему?

2. Назовите все нечётные числа, удовлетворяющие неравенству .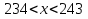

3. Назовите числа кратные числу 13, 39.

Если утверждение, верно, пишите в строчку на маленьких листочках цифру 1, если нет – 0. Должно получится пятизначное число.

1. Число 1 – ни составное, ни простое число.

2. Натуральное число называют составным, если оно имеет только два делителя.

3. Делителем натурального числа a называют натуральное число, на которое a делится без остатка.

4. Если сумма цифр делится на 9, то и число делится на 9.

5. Если запись оканчивается цифрой 3, то и число делится на 3 без остатка.

1. Игра «Самый внимательный»

45, 67, 38, 650, 735, 226, 10000, 539, 3255.

А) Хлопните в ладоши, если число кратно 2.

Б) Замяукайте, если число кратно 5.

В) Топайте ногами, если число кратно 10.

Почему вы одновременно хлопали, мяукали и топали ногами?

1. Закрепление знаний

Корабль отправляется по маршруту. На экране примеры (1, 2 и 5 разложив числа на простые множители, найти НОК; в 3 и 4 разложение уже известно).

1. НОК (14,18)=126

2. Нок (28,42)=84

3. a=24·32   и  b=22·32·5                       НОК(а;b)=24·32·5=720

4. c=2·32·11  и  t=23·3·11                    НОК(с;t)=23·32·11=792

5. Нок(24, 35)=840