Некоторые приёмы решения функциональных уравнений
В математике функциональным уравнением называется уравнение, выражающее связь между значением функции (или функций) в одной точке с ее значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Часто встречаются на различных математических соревнованиях и экзаменах по математике в ВУЗах с усиленной подготовкой по математике.
Решение функциональных уравнений может быть очень трудным, но существуют некоторые общие методы их решения. Рассмотрим их на примере нескольких задач.
Задача 1. Задана функция f, причём  для всех рациональных чисел х, у. Известно, что
для всех рациональных чисел х, у. Известно, что  Найдите
Найдите 
Чёрт, здесь же практически ничего не известно!!! Вот бы получить выражение  через какие-то величины… Попробуем…
через какие-то величины… Попробуем…
Ну, например, х = 2х – х. Ага, получится  Отсюда мы получим, что
Отсюда мы получим, что  . Уже лучше! И что? Ну, например,
. Уже лучше! И что? Ну, например,  , а дальше…
, а дальше…  А дальше? Ведь 6 из 1 удвоением не получить… А утроением?!
А дальше? Ведь 6 из 1 удвоением не получить… А утроением?!
 . Ого!
. Ого!

 .
.
Задача 2. Задана функция f, причём  для всех рациональных чисел х, у. Известно, что
для всех рациональных чисел х, у. Известно, что  Найдите
Найдите 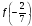
Ну, это я теперь махом!
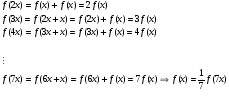
Во блин! Как же мне из положительных чисел отрицательные получить??

Что, легче стало? А если так?
 Ё-моё!!! Так функция же нечётна!!! Ну, тогда всё понятно
Ё-моё!!! Так функция же нечётна!!! Ну, тогда всё понятно

Задача 3. Найти функцию, если известно, что 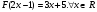
Хм, наверное, здесь проблем не будет, если ввести дополнительную переменную. Пусть
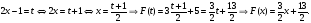
Задача 4. Для некоторой функции известно, что  Найти F(1), F(2), F(t).
Найти F(1), F(2), F(t).
Ну, с F(1), положим, проблем не будет…  Что-то возиться, как в первых двух задачах, неохота, чтобы получить F(2)… А что, если сразу найти F(t)?!
Что-то возиться, как в первых двух задачах, неохота, чтобы получить F(2)… А что, если сразу найти F(t)?!
Пусть  . Тогда
. Тогда  Пусть
Пусть  Тогда Пусть
Тогда Пусть  Получается система уравнений
Получается система уравнений
Проверка показывает, что решение найдено верно.
Задача 5. 
 . Найти
. Найти  .
.
Пусть
Чтобы найти остальные частные решения, найдём сразу общее по тому же методу.
Пусть  . Тогда
. Тогда  Пусть
Пусть  Тогда Сделаем замену и решим получившуюся систему уравнений.
Тогда Сделаем замену и решим получившуюся систему уравнений.
. Значит, 
Задача 6. Найти функцию f, если известно, что при всех х ≠ ±1 
Используем приём из задачи 3. Пусть  Подставив полученное выражение в исходные данные, получим
Подставив полученное выражение в исходные данные, получим 
Задача 7. Найдите функцию f, если известно, что f(0) = 1 и при всех х ≠ ±1 
Пусть  Тогда
Тогда  Если же
Если же  то
то  Обозначив
Обозначив  получим систему уравнений.
получим систему уравнений.
Т. е. 
Задача 8. Решить функциональное уравнение  где
где 
Т. к. х и у принимают произвольные значения, возьмём x = 2t и y = t. Тогда уравнение перепишется в виде  Сделав ещё одну замену u = 2t, получим
Сделав ещё одну замену u = 2t, получим 
Задача 9. Решить функциональное уравнение  где х, у, принимают любые действительные значения.
где х, у, принимают любые действительные значения.
Возьмём x = y = t. Тогда  Сделав замену
Сделав замену  , решим получившееся уравнение как квадратное относительно а.
, решим получившееся уравнение как квадратное относительно а. 
Задача 10. Решить функциональное уравнение  где х и у принимают любые действительные значения.
где х и у принимают любые действительные значения.
Т. к. х и у могут принимать любые значения, возьмём x = t, y = 0. Получим  Если взять
Если взять  то
то  Аналогично будем получать, что
Аналогично будем получать, что  Таким образом замечаем, что f(0) – некоторая константа, а сама функция имеет вид f(x) = x + c, где с – некоторая константа, в частности с = f(0).
Таким образом замечаем, что f(0) – некоторая константа, а сама функция имеет вид f(x) = x + c, где с – некоторая константа, в частности с = f(0).
Задача 11. Решить функциональное уравнение  (х ≠ 0, х ≠ 1).
(х ≠ 0, х ≠ 1).
Пусть  Тогда
Тогда  Пусть
Пусть  Тогда
Тогда  Наконец, пусть
Наконец, пусть  Тогда
Тогда  Сделаем замены
Сделаем замены  Получим систему уравнений.
Получим систему уравнений.
Значит,







 для всех рациональных чисел х, у. Известно, что
для всех рациональных чисел х, у. Известно, что  Найдите
Найдите 
 через какие-то величины… Попробуем…
через какие-то величины… Попробуем… Отсюда мы получим, что
Отсюда мы получим, что  . Уже лучше! И что? Ну, например,
. Уже лучше! И что? Ну, например,  , а дальше…
, а дальше…  А дальше? Ведь 6 из 1 удвоением не получить… А утроением?!
А дальше? Ведь 6 из 1 удвоением не получить… А утроением?!  . Ого!
. Ого!
 .
.  для всех рациональных чисел х, у. Известно, что
для всех рациональных чисел х, у. Известно, что  Найдите
Найдите 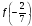
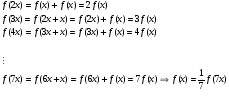

 Ё-моё!!! Так функция же нечётна!!! Ну, тогда всё понятно
Ё-моё!!! Так функция же нечётна!!! Ну, тогда всё понятно 
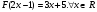
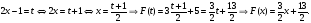
 Найти F(1), F(2), F(t).
Найти F(1), F(2), F(t). Что-то возиться, как в первых двух задачах, неохота, чтобы получить F(2)… А что, если сразу найти F(t)?!
Что-то возиться, как в первых двух задачах, неохота, чтобы получить F(2)… А что, если сразу найти F(t)?! . Тогда
. Тогда  Пусть
Пусть  Тогда Пусть
Тогда Пусть 









