Неравенства с двумя переменными

Цель урока:

Обучающая:

• закрепить понятие неравенства с двумя переменными и его решения;

• закрепить умение решать линейные неравенства с двумя переменными;

• изображать решение неравенств на координатной плоскости XOY

Развивающая:

• развивать элементы логического мышления;

• развить умение пользоваться полученной информацией;

• развить интерес к математике;

• развивать навыки работы в группе и самостоятельно.

Воспитательная:

воспитывать внимательность, самостоятельность, мышление, воспитывать чувство ответственности

Деятельность учителя

Деятельность обучающихся

Наглядности

8 мин.

I. Организационный момент.

Эмоциональный настрой урока. Рукопожатие учащихся.

1) Показываю учащимся две карточки и задаю вопрос: в чём сходство и различие этих двух карточек? Какова тема нашего урока?

2) С помощью приёма «Корзина» идей и понятий учащиеся выписывают ключевые понятия данной темы урока.

А какова цель нашего урока?

Ученики Выполняют поставленную цель.

Лист бумаги

Карточки

Фломастеры

8 мин.

II. Актуализация знаний.

1. Учащие заполняют таблицу.

Применяется метод “Верю-не верю”

Учащиеся по часовой стрелке меняются работами. Проводится взаимопроверка работ.

Демонстрируют свои знания, умения

Оценивают работу своих одноклассников

Индивидуальные карточки

15 мин.

III. Закрепление ранее изученного материала.

Определение: Выражения, составленные с помощью чисел, двух переменных, знаков действий и знаков сравнения называются неравенствами с двумя переменными.

1. С помощью приема «Кластер» - учащиеся составляют Алгоритм решения неравенств с двумя переменными. Выделяется 5 минут.

Поочерёдно группы у доски озвучивают свои ответы.

Затем учитель зачитывает Алгоритм и сравниваем ответы.

АЛГОРИТМ:

1. Заменить знак неравенства на равно;

2. Выразить одну переменную через другую;

3. Построить график полученного уравнения;

4. Выбрать по одной точке из полученных полуплоскостей.

5. Проверить, удовлетворяют ли их координаты неравенству.

6. Выбрать удовлетворяющую неравенству точку.

2. Ребята, а теперь давай те каждая группа, с помощью Алгоритма решений, на примерах вспомнит, как изображается множество решений неравенства с двумя переменными на координатной плоскости.

Каждая группа получает конверт с заданием и ватман.

1 группа

Изобразить на координатной плоскости XOY фигуру, состоящую из точек, координаты которых удовлетворяют неравенству 2у+3х≤6.

Решение.

1.Заменить знак неравенства на равно: 2у+3х=6

2. Выразить переменную у через переменную х:

2у=6-3х

у=3-1,5х

3. Построить график полученного уравнения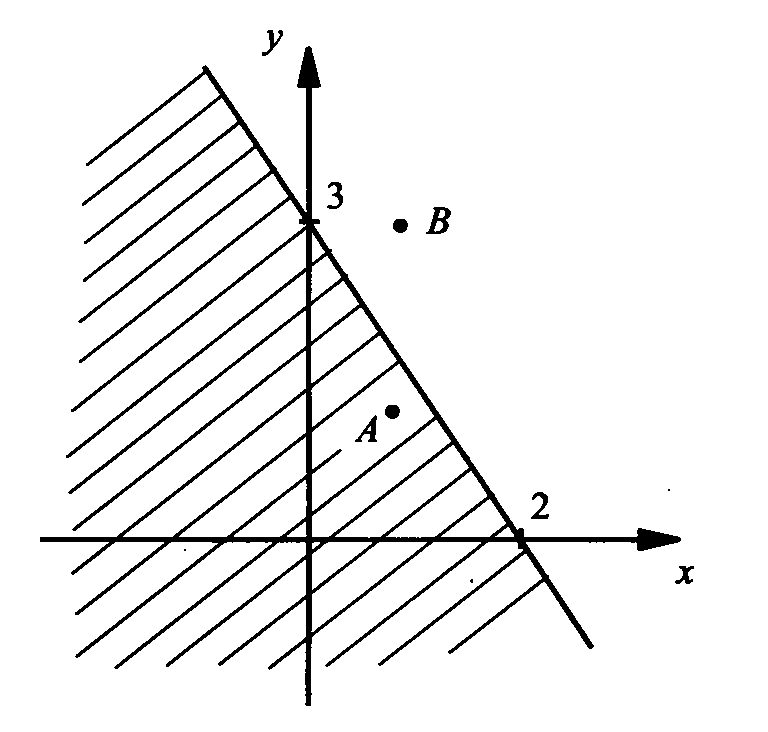

Прямая разбивает множество всех точек координатной плоскости на точки, расположенные ниже ее, и точки, расположенные выше ее. Возьмем из каждой области по контрольной точке: А(1;1), В(1;3).

Координаты точки А удовлетворяют данному неравенству 2у+3х≤6,

2·1+3·1≤6,

5≤6

Координаты точки В не удовлетворяют данному неравенству 2у+3х≤6,

2·3+3·1≤6

9≤6

2 группа

Изобразить на координатной плоскости XOY фигуру , состоящую из точек, координаты которых удовлетворяют неравенству у+1 ≥ х²

Решение.

1.Заменить знак неравенства на равно: у +1 = х²

2. Выразить переменную у через переменную х: у = х² - 1

3. Построить график полученного уравнения

В

А

Парабола разбивает множество всех точек координатной плоскости на точки, расположенные внутри ее, и точки, расположенные снаружи ее. Возьмем из каждой области по контрольной точке: А(1;3), В(3;1).

Координаты точки А удовлетворяют данному неравенству: 3+1 ˃ 1²

4 ˃ 1

Координаты точки В не удовлетворяют данному неравенству: 1 + 1 ˃ 3²

2 ˃ 9

3 группа

Изобразить на координатной плоскости XOY фигуру , состоящую из точек, координаты которых удовлетворяют неравенству х² + у²

Решение.

1.Заменить знак неравенства на равно: х² + у² = 4

2. Определить, какая фигура задаётся таким уравнением:

х² + y² = 4 – уравнение окружности, с центром в начале координат, R = 2

3. Построить данную фигуру в системе координат и выделить область, соответствующую знаку неравенства

В

А

Окружность разбивает множество всех точек координатной плоскости на точки, расположенные внутри ее, и точки, расположенные снаружи ее. Возьмем из каждой области по контрольной точке: А(-1;1), В(3;-1).

Координаты точки А удовлетворяют данному неравенству:

(-1)² + 1²

1 + 1

2

Координаты точки В не удовлетворяют данному неравенству: 3² + (-1)²

9 + 1

10

4 группа

Изобразить на координатной плоскости XOY фигуру , состоящую из точек, координаты которых удовлетворяют неравенству у – 2х

1.Заменить знак неравенства на равно: у – 2х = 1

2. Выразить переменную у через переменную х:

у = 2х + 1

3. Построить график полученного уравнения

2

3

О

у

х

В

А

Прямая разбивает множество всех точек координатной плоскости на точки, расположенные ниже ее, и точки, расположенные выше ее. Возьмем из каждой области по контрольной точке: А(1;1), В(-2;2).

Координаты точки А удовлетворяют данному неравенству

1 - 2·1

-1

Координаты точки В не удовлетворяют данному неравенству : 2 – 2 · (-2)

2 + 4

6

Работая в группах,

ученики обсуждают,

записываю,

рассказываю.

Ватман

Фломастеры

Тетрадь

Доска

8 мин.

IV. Итог урока.

Организует систематизацию и обобщение совместных достижений:

1. Проговорить определение неравенства с двумя переменными.

2. Озвучить алгоритм решения неравенств.

Рефлексия.

Учащимся предлагается составить «Синквейн»

Слово «синквейн» – французское, обозначающее «5 строк».

Для его написания существуют правила.

Тема Синквейна: Неравенство

Рассказывают определение и алгоритм.

Составляю синквейн по группам. Зачитываю свои работы.

Лист бумаги

Карандаши

Фломастеры

1 мин.

V. Домашнее задание. Объясняю особенности выполнения домашней работы.

Составить своё собственное неравенство и решить его.

Записывают домашнюю работу в дневниках.